Sprawdzian 2 Gimnazjum Rodzaje Graniastosłupów

Czy zdarza Ci się spoglądać na budynki, pudełka, a nawet kostki do gry i zastanawiać się, co łączy te pozornie różne przedmioty? A może przygotowujesz się do sprawdzianu z matematyki i czujesz, że temat graniastosłupów wydaje się być kolejną zmorą, która spędza Ci sen z powiek? Rozumiemy to doskonale. Świat geometrii przestrzennej bywa czasem niełatwy do rozgryzienia, zwłaszcza gdy trzeba opanować różnorodność kształtów i ich charakterystyk. Ale spokojnie, nie jesteś sam!

Ten artykuł jest Twoim przewodnikiem po fascynującym świecie graniastosłupów. Postaramy się rozwiać wszelkie wątpliwości, wyjaśnić kluczowe pojęcia i pokazać, że matematyka wcale nie musi być straszna. Przygotuj się na podróż, która rozjaśni Ci umysł i sprawi, że spojrzysz na otaczający Cię świat z nowej, geometrycznej perspektywy.

Zrozumieć Podstawy: Czym Właściwie Jest Graniastosłup?

Zanim zagłębimy się w konkretne typy graniastosłupów, ustalmy wspólnie, czym one są. W najprostszym ujęciu, graniastosłup to bryła geometryczna, która ma dwie identyczne, równoległe podstawy (tzw. ściany podstawowe) oraz ściany boczne, które są równoległobokami. Pomyśl o tym jak o "przedłużeniu" kształtu podstawy w górę, tworząc trójwymiarową przestrzeń.

Wyobraź sobie, że bierzesz kartkę papieru w kształcie trójkąta, a następnie "wyciągasz" ją prostopadle do płaszczyzny kartki na pewną wysokość. Otrzymasz w ten sposób graniastosłup trójkątny. To właśnie ta powtarzalność i równoległość podstaw definiuje graniastosłup.

Ważne jest również to, że wszystkie ściany boczne graniastosłupa są równoległobokami. Jeśli ściany te są dodatkowo prostokątami, mówimy o graniastosłupie prostym. Gdy ściany boczne są pochylone, mamy do czynienia z graniastosłupem nachylonym. Dla celów szkolnych, najczęściej skupiamy się na graniastosłupach prostych, ponieważ są one łatwiejsze do analizy i obliczeń.

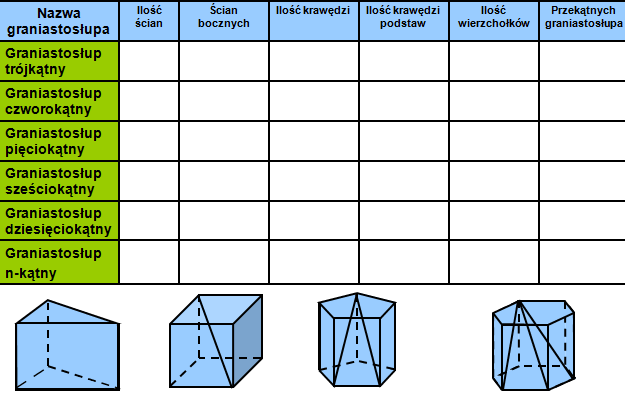
Kluczowe Elementy Graniastosłupa

Aby pewnie poruszać się w świecie graniastosłupów, warto znać ich podstawowe elementy:

Podstawy: Dwie identyczne i równoległe figury płaskie, które determinują nazwę graniastosłupa (np. trójkąt, kwadrat, sześciokąt).
Ściany boczne: Równoległoboki łączące boki obu podstaw.
Krawędzie: Odcinki, które są bokami ścian. Dzielą się na krawędzie podstaw (łączące wierzchołki w jednej podstawie) oraz krawędzie boczne (łączące odpowiadające sobie wierzchołki obu podstaw).
Wierzchołki: Punkty, w których spotykają się krawędzie.
Wysokość: Odległość między płaszczyznami obu podstaw. W graniastosłupie prostym, wysokość jest równa długości krawędzi bocznej.

Zrozumienie tych elementów jest fundamentem do dalszej nauki. Bez nich, trudno będzie mówić o objętości czy polu powierzchni.

Główne Rodzaje Graniastosłupów – Podział wg Kształtu Podstawy

Nazwa graniastosłupa zależy od kształtu jego podstawy. To właśnie ta cecha wyróżnia poszczególne typy:

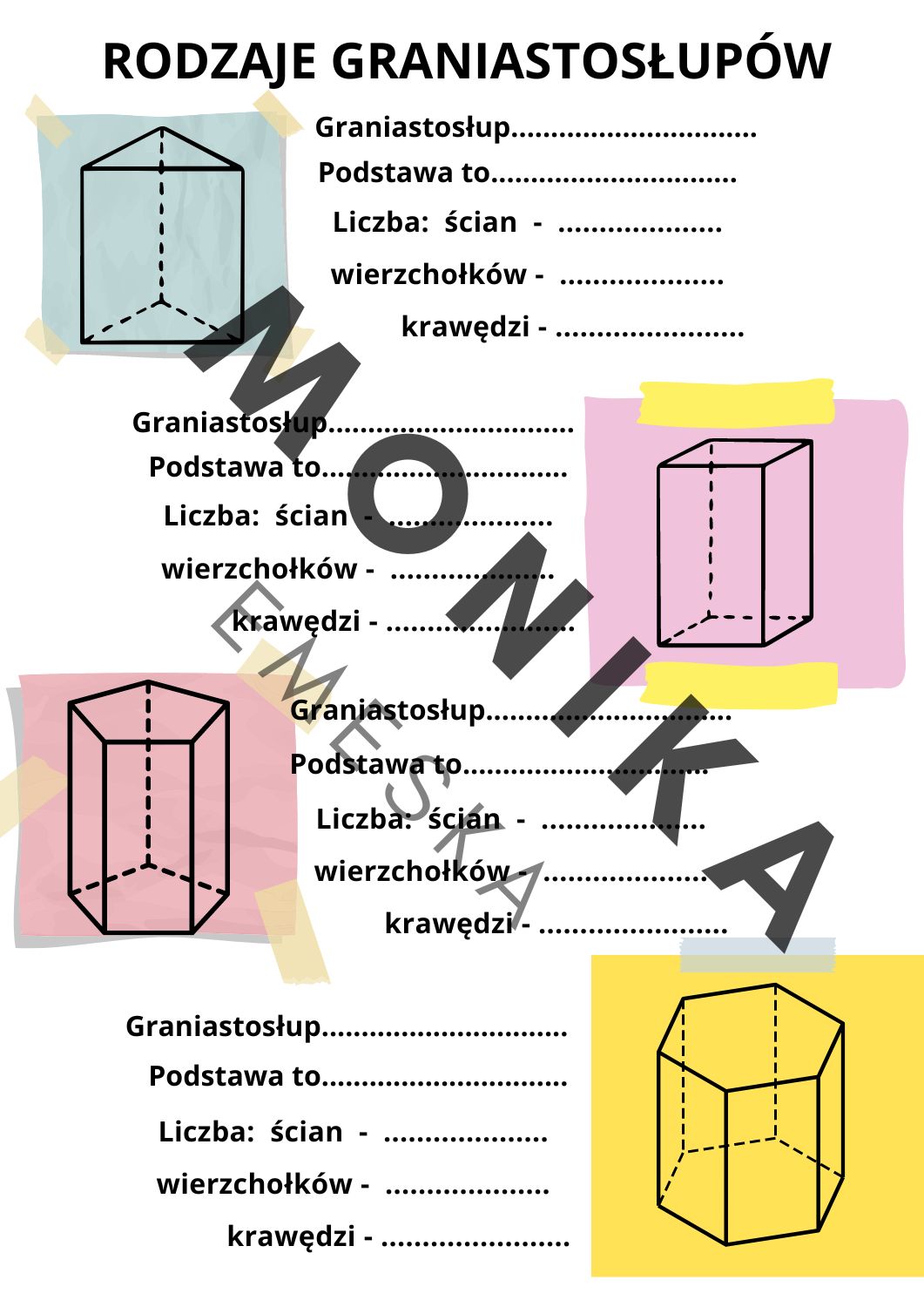
Graniastosłup Trójkątny

Jak sama nazwa wskazuje, jego podstawami są trójkąty. Ściany boczne to zazwyczaj prostokąty (w przypadku graniastosłupa prostego).

Kiedy go spotkasz? Wyobraź sobie namiot w kształcie pryzmatu lub kawałek sera w kształcie klina. Nawet pudełko na prezent w kształcie takiego klina będzie graniastosłupem trójkątnym.

Graniastosłup Czworokątny

Podstawami są czworokąty. Tutaj mamy kilka ważnych podtypów:

Graniastosłup Prostopadłościenny: Podstawami są prostokąty. Ma on wszystkie ściany boczne jako prostokąty. Jest to jeden z najczęściej spotykanych graniastosłupów w życiu codziennym.
Graniastosłup Sześcienny (Sześcian): To szczególny przypadek prostopadłościanu, w którym wszystkie krawędzie mają tę samą długość, a wszystkie ściany są kwadratami. Kostka do gry to idealny przykład sześcianu.
Graniastosłup Kwadratowy: Podstawami są kwadraty, a ściany boczne są prostokątami. Jest to graniastosłup prostokątny, ale z kwadratową podstawą.

Kiedy je spotkasz? Pudełka na buty, cegły, budynki mieszkalne (często mają prostopadłościenny kształt), kostki do gry – to wszystko przykłady graniastosłupów czworokątnych.

Graniastosłup Pięciokątny

Jego podstawami są pięciokąty. Ściany boczne to pięć równoległoboków (lub prostokątów w graniastosłupie prostym).

Kiedy go spotkasz? Choć rzadziej niż prostopadłościany, mogą pojawiać się w architekturze, np. fragmenty budowli czy specjalistyczne pojemniki.

Graniastosłup Sześciokątny

Podstawami są sześciokąty. Ma sześć ścian bocznych.

Kiedy go spotkasz? Znane plastry miodu u pszczół to doskonały przykład graniastosłupa sześciokątnego (choć zazwyczaj mają podstawy otwarte). W architekturze można spotkać elementy o takiej formie.

Graniastosłupy o Wielokątach o Większej Liczbie Boków

Możemy tworzyć graniastosłupy o podstawach będących siedmiokątami, ośmiokątami, dziesięciokątami i tak dalej. Zasada jest ta sama: dwie identyczne, równoległe figury wielokątne jako podstawy i równoległoboki jako ściany boczne.

Im więcej boków ma wielokąt w podstawie, tym bardziej bryła zaczyna przypominać walec. To ciekawe przejście geometryczne pokazuje, jak różne kształty mogą się wzajemnie uzupełniać.

Graniastosłup Prostych i Nachylony – Różnica, Która Ma Znaczenie

Wspominaliśmy już o graniastosłupach prostych i nachylonych. Teraz przyjrzyjmy się tej różnicy dokładniej:

Graniastosłup Prosty: W tym typie graniastosłupa, krawędzie boczne są prostopadłe do płaszczyzn podstaw. To oznacza, że ściany boczne są prostokątami. W praktyce ułatwia to wszelkie obliczenia, ponieważ wysokość graniastosłupa jest równa długości krawędzi bocznej.
Graniastosłup Nachylony: Tutaj krawędzie boczne nie są prostopadłe do płaszczyzn podstaw. Ściany boczne są równoległobokami (niekoniecznie prostokątami). Obliczanie wysokości w graniastosłupie nachylonym jest nieco bardziej skomplikowane, ponieważ wymaga znalezienia odległości między płaszczyznami podstaw, która nie jest tożsama z długością krawędzi bocznej.

W kontekście sprawdzianów szkolnych, zdecydowana większość zadań będzie dotyczyć graniastosłupów prostych, a w szczególności tych o podstawach będących regularnymi wielokątami (kwadrat, sześciokąt) lub prostymi figurami (trójkąt, prostokąt).

Dlaczego Warto Zrozumieć Graniastosłupy?

Poza tym, że są one ważnym elementem programu nauczania, zrozumienie graniastosłupów ma praktyczne zastosowanie:

Architektura i Budownictwo: Wiele budynków, od domów jednorodzinnych po wieżowce, ma bryły oparte na graniastosłupach. Zrozumienie ich kształtu i objętości jest kluczowe przy projektowaniu i kosztorysowaniu.
Przemysł i Produkcja: Opakowania produktów, materiały budowlane (np. cegły, płyty), a nawet elementy maszyn często mają kształt graniastosłupów.
Rozwój Myślenia Przestrzennego: Nauka geometrii przestrzennej, w tym graniastosłupów, doskonale rozwija umiejętność wyobrażania sobie i analizowania obiektów w trzech wymiarach. To kompetencja ceniona w wielu dziedzinach życia i pracy.
Matematyka na Co Dzień: Nawet proste obliczenia objętości pudełka, w którym coś kupujesz, czy szacowanie ilości materiału potrzebnego do budowy czegoś, opierają się na zasadach dotyczących graniastosłupów.

Jak pokazują badania nad rozwojem poznawczym, nauka geometrii przestrzennej znacząco wpływa na zdolności problem-solving oraz rozumowanie logiczne. Według raportu organizacji zajmujących się edukacją matematyczną, uczniowie lepiej radzący sobie z zadaniami przestrzennymi często osiągają lepsze wyniki w innych obszarach nauk ścisłych.

Jak Przygotować Się do Sprawdzianu? Praktyczne Wskazówki

Opanowanie tematu graniastosłupów do sprawdzianu może wydawać się wyzwaniem, ale z odpowiednim podejściem jest jak najbardziej osiągalne. Oto kilka sprawdzonych metod:

Wizualizacja jest Kluczem:
- Rysuj! Nie bój się szkicować graniastosłupów. Rysuj podstawy, łącz je krawędziami bocznymi. Ćwicz rysowanie graniastosłupów prostych i nachylonych.
- Używaj Obiektów z Życia Codziennego: Znajdź w domu przedmioty o kształcie graniastosłupów (pudełka, książki, kostki do gry) i analizuj ich kształt. Zastanów się, jakim typem graniastosłupa są.
- Modele Geometryczne: Jeśli masz możliwość, skorzystaj z gotowych modeli geometrycznych. Manipulowanie nimi w rękach pomaga lepiej zrozumieć ich budowę.
Poznaj Formuły na Pamięć i Zrozum Je:
- Pole Podstawy (Pp): W zależności od kształtu podstawy (trójkąt, kwadrat, prostokąt, sześciokąt), zastosuj odpowiedni wzór.
- Pole Powierzchni Bocznej (Pb): W graniastosłupie prostym jest to iloczyn obwodu podstawy i wysokości (Pb = Obwód_podstawy * h).
- Całkowite Pole Powierzchni (Pc): To suma pól obu podstaw i pola powierzchni bocznej (Pc = 2 * Pp + Pb).
- Objętość (V): Wzór jest prosty: objętość graniastosłupa to iloczyn pola podstawy i wysokości (V = Pp * h).
Nie ucz się ich tylko na pamięć, ale staraj się zrozumieć, skąd się biorą te wzory.
Ćwicz Rozwiązywanie Zadań:
- Zacznij od Prostych Przykładów: Rozwiązuj zadania, w których dane są wszystkie wymiary i trzeba obliczyć pole lub objętość.
- Przechodź do Trudniejszych: Stopniowo zwiększaj poziom trudności, rozwiązując zadania, w których musisz najpierw obliczyć brakujące boki, wysokości lub pola.
- Rodzaje Zadań: Przygotuj się na zadania dotyczące różnych typów graniastosłupów (trójkątnych, czworokątnych, sześciokątnych), zarówno prostych, jak i (rzadziej) nachylonych.
Powtarzalność jest kluczem do sukcesu. Im więcej zadań rozwiążesz, tym pewniej będziesz się czuł.
Korzystaj z Pomocy Naukowych:
- Podręcznik i Zeszyt Ćwiczeń: To Twoje podstawowe źródła wiedzy. Dokładnie przeanalizuj przykłady i rozwiązane zadania.
- Materiały Online: Istnieje wiele stron internetowych i kanałów YouTube oferujących lekcje i ćwiczenia z geometrii.
- Nauczyciel i Koledzy: Nie wahaj się pytać nauczyciela o wyjaśnienie wątpliwości. Warto też wspólnie z kolegami rozwiązywać zadania i dyskutować.

Pamiętaj, że przygotowanie do sprawdzianu to proces. Systematyczna praca i zrozumienie materiału przyniosą najlepsze efekty.

Podsumowanie – Graniastosłupy w Pigułce

Świat graniastosłupów, choć na pierwszy rzut oka może wydawać się skomplikowany, jest logiczny i spójny. Od prostych pudełek po bardziej złożone bryły, wszystkie one dzielą te same fundamentalne zasady. Kluczem do sukcesu jest zrozumienie ich budowy, poznanie podstawowych elementów i zapamiętanie (a przede wszystkim zrozumienie) wzorów na obliczenie ich pola i objętości.

Niezależnie od tego, czy jest to graniastosłup trójkątny, czworokątny (w tym prostopadłościan i sześcian), pięciokątny, czy sześciokątny, zasady pozostają te same. Poświęć czas na wizualizację, ćwicz regularnie i nie bój się zadawać pytań.

Mamy nadzieję, że ten artykuł rozjaśnił Ci zagadnienie rodzajów graniastosłupów i sprawił, że przygotowanie do sprawdzianu stanie się łatwiejsze i bardziej efektywne. Pamiętaj, że matematyka otacza nas wszędzie, a zrozumienie jej zasad otwiera nam drzwi do lepszego poznawania świata. Powodzenia!