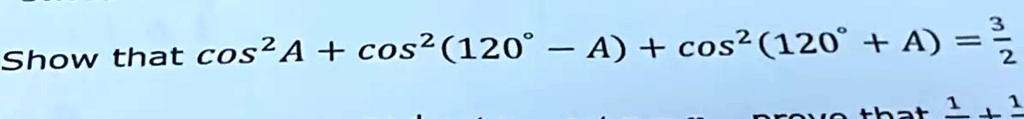Sin 2 120 Cos 2 120

Sin2(120°) + Cos2(120°) to wyrażenie trygonometryczne, którego wartość można obliczyć na podstawie podstawowej tożsamości trygonometrycznej. Tożsamość ta mówi, że dla każdego kąta α, sin2(α) + cos2(α) = 1.
Kluczowym aspektem jest tutaj sama tożsamość. Niezależnie od wartości kąta α, suma kwadratów sinusa i cosinusa tego kąta zawsze będzie równa 1. Oznacza to, że nie musimy obliczać wartości sinusa i cosinusa 120 stopni, aby znaleźć wynik.
Dowód tożsamości opiera się na twierdzeniu Pitagorasa w trójkącie prostokątnym. Wyobraźmy sobie trójkąt prostokątny o przeciwprostokątnej równej 1. Wtedy sinus kąta α jest równy długości przeciwległej przyprostokątnej, a cosinus kąta α jest równy długości przyległej przyprostokątnej. Zgodnie z twierdzeniem Pitagorasa, suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej, czyli sin2(α) + cos2(α) = 12 = 1.
Wartość kąta 120 stopni jest istotna jedynie w kontekście obliczania poszczególnych wartości sinusa i cosinusa, jeśli nie korzystamy bezpośrednio z tożsamości. Kąt 120 stopni leży w drugiej ćwiartce układu współrzędnych, gdzie sinus jest dodatni, a cosinus ujemny. Jednak dla naszego wyrażenia sin2(120°) + cos2(120°), konkretne wartości sinusa i cosinusa nie mają znaczenia, ponieważ działamy na ich kwadratach, a wynik zawsze będzie równy 1.
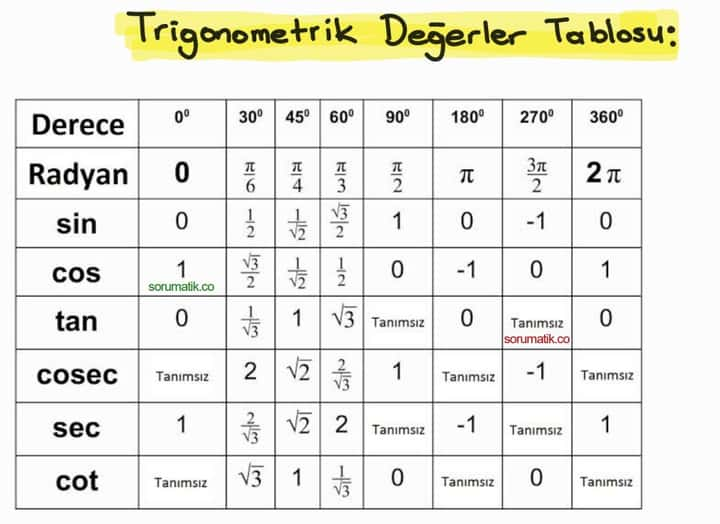
Przykład 1: Rozważmy kąt 30 stopni. sin2(30°) + cos2(30°) = (1/2)2 + (√3/2)2 = 1/4 + 3/4 = 1.
Przykład 2: Rozważmy kąt 0 stopni. sin2(0°) + cos2(0°) = (0)2 + (1)2 = 0 + 1 = 1.
Podsumowując, sin2(120°) + cos2(120°) = 1, ponieważ jest to bezpośrednia konsekwencja fundamentalnej tożsamości trygonometrycznej.
Zastosowanie w praktyce: Tożsamość trygonometryczna sin2(α) + cos2(α) = 1 jest szeroko wykorzystywana w różnych dziedzinach, takich jak fizyka (np. w analizie ruchu harmonicznego), inżynieria (np. w obliczeniach związanych z falami i drganiami), a także w grafice komputerowej (np. w transformacjach współrzędnych).