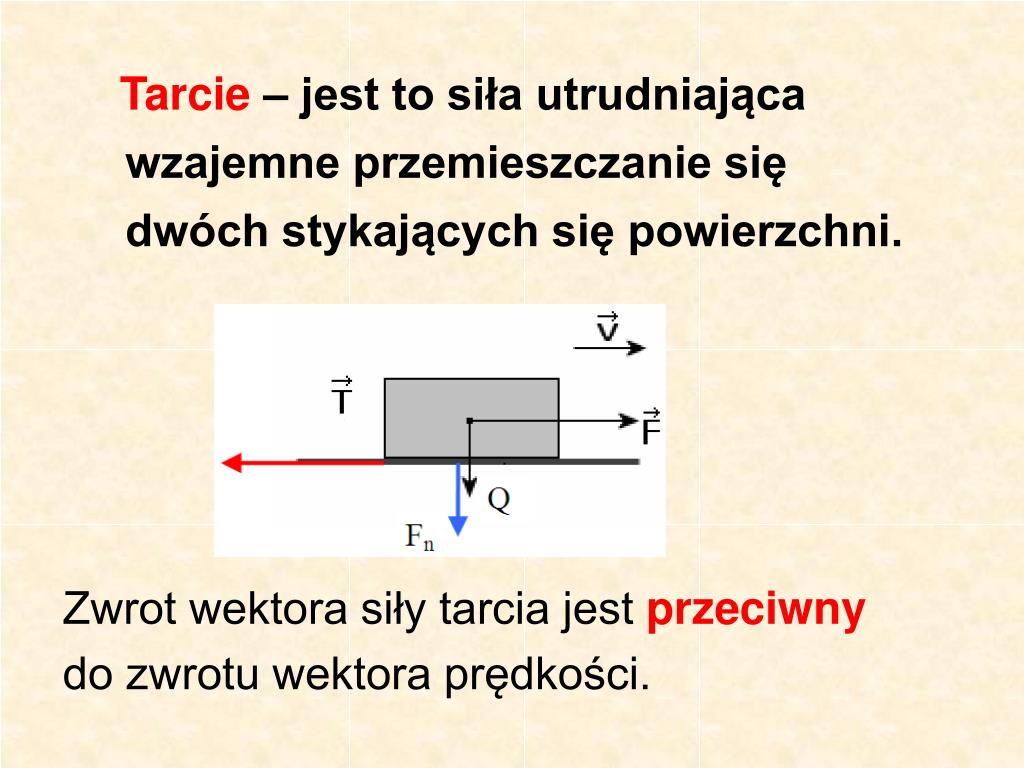
Siła Oporu Powietrza Wzór
Siła oporu powietrza to siła działająca przeciwnie do kierunku ruchu obiektu w powietrzu. Można ją obliczyć za pomocą wzoru: F = 1/2 * ρ * v² * Cd * A.
Rozłóżmy ten wzór krok po kroku:
Krok 1: ρ (Rho) - Gęstość powietrza. To miara masy powietrza na jednostkę objętości. Zwykle wyrażana w kg/m³. Przyjmuje się, że w standardowych warunkach (temperatura pokojowa i ciśnienie atmosferyczne) wynosi około 1.225 kg/m³. Wyższa gęstość powietrza oznacza większy opór. Przykład: Dla ρ = 1.225 kg/m³, wpisujemy tę wartość bezpośrednio do wzoru.
Krok 2: v (v) - Prędkość obiektu. To prędkość, z jaką obiekt porusza się w powietrzu. Im szybciej obiekt się porusza, tym większy opór powietrza. Jest wyrażana w metrach na sekundę (m/s). Przykład: Jeśli rower jedzie z prędkością 10 m/s, to v = 10 m/s. Pamiętaj, aby podnieść tę wartość do kwadratu (v²).
Krok 3: Cd (Cd) - Współczynnik oporu. To bezwymiarowa liczba, która zależy od kształtu obiektu. Mówi nam, jak aerodynamiczny jest dany obiekt. Bardziej opływowe kształty mają niższy współczynnik oporu. Przykłady: Samochód może mieć Cd = 0.3, spadochron Cd = 1.2. Wartości Cd są często znajdowane w tabelach referencyjnych dla różnych kształtów.
Krok 4: A (A) - Powierzchnia przekroju poprzecznego. To powierzchnia obiektu prostopadła do kierunku ruchu. Im większa powierzchnia, tym większy opór powietrza. Wyrażana w metrach kwadratowych (m²). Przykład: Jeśli spadochron ma powierzchnię 5 m², to A = 5 m². Dla piłki o promieniu 0.1 m, powierzchnia przekroju (koła) to π * (0.1)² ≈ 0.0314 m².
Krok 5: Obliczenia. Po zidentyfikowaniu wszystkich wartości, po prostu podstaw je do wzoru i wykonaj obliczenia. Pamiętaj o kolejności działań (najpierw potęgowanie, potem mnożenie).
Przykład: Załóżmy, że mamy piłkę (Cd = 0.47) o powierzchni przekroju 0.0314 m² poruszającą się z prędkością 5 m/s w powietrzu o gęstości 1.225 kg/m³. Siła oporu powietrza wynosi: F = 1/2 * 1.225 kg/m³ * (5 m/s)² * 0.47 * 0.0314 m² ≈ 0.023 N.
Dlaczego to jest ważne? Zrozumienie i obliczanie siły oporu powietrza jest kluczowe w wielu dziedzinach. Na przykład, w inżynierii lotniczej, pozwala na projektowanie bardziej efektywnych samolotów, zmniejszając zużycie paliwa. Również w sporcie, np. w kolarstwie, minimalizowanie oporu powietrza pozwala sportowcom osiągać lepsze wyniki poprzez zastosowanie aerodynamicznych strojów i pozycji.