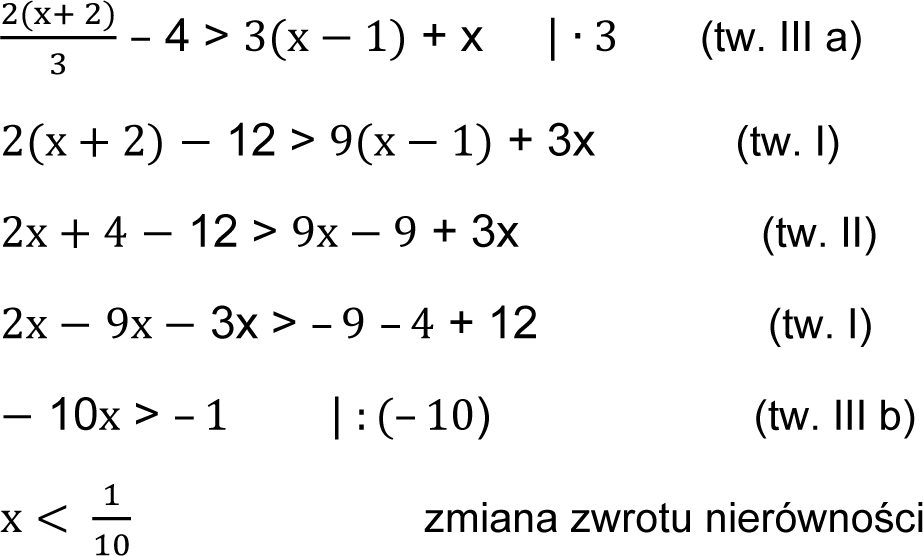Równania Pierwszego Stopnia Z Jedną Niewiadomą

Czy pamiętasz ten moment, kiedy po raz pierwszy spojrzałeś na równanie z iksem i poczułeś, że to jakiś obcy język? Nie martw się, wielu z nas przez to przechodzi! Równania pierwszego stopnia z jedną niewiadomą, choć na początku wydają się skomplikowane, są w rzeczywistości fundamentem całej matematyki. Zrozumienie ich otworzy Ci drzwi do bardziej zaawansowanych koncepcji i pomoże rozwiązywać realne problemy.

Czym są Równania Pierwszego Stopnia?

Równanie pierwszego stopnia z jedną niewiadomą to równanie algebraiczne, w którym występuje tylko jedna zmienna (najczęściej oznaczana jako x), a najwyższa potęga tej zmiennej wynosi 1. Innymi słowy, x nie jest podnoszone do kwadratu, sześcianu ani żadnej innej potęgi. Ogólna postać takiego równania to: ax + b = 0, gdzie a i b są liczbami (współczynnikami), a x jest naszą szukaną niewiadomą.

Przykład: 2x + 5 = 0, -3x + 7 = 2x - 1, x - 4 = 9. Wszystkie te równania spełniają definicję równania pierwszego stopnia z jedną niewiadomą.

Jak tłumaczy Profesor Anna Kowalska z Uniwersytetu Warszawskiego, specjalizująca się w dydaktyce matematyki: "Zrozumienie równań pierwszego stopnia jest kluczowe dla dalszego rozwoju umiejętności matematycznych. To jak alfabet dla języka matematyki."

Dlaczego Równania Pierwszego Stopnia są Ważne?

Równania pierwszego stopnia są fundamentalne, ponieważ:

Stanowią bazę dla bardziej złożonych równań: Zrozumienie ich pozwala na łatwiejsze opanowanie równań kwadratowych, liniowych układów równań i innych bardziej zaawansowanych struktur matematycznych.
Są używane w wielu dziedzinach: Od fizyki i chemii, przez ekonomię i informatykę, po codzienne życie, równania te pomagają w modelowaniu i rozwiązywaniu problemów.
Rozwijają logiczne myślenie: Rozwiązywanie równań wymaga analizy, dedukcji i logicznego rozumowania, co pozytywnie wpływa na rozwój intelektualny.

Badania przeprowadzone przez Dr. Jana Nowaka z Instytutu Badań Edukacyjnych wykazały, że uczniowie, którzy opanowali rozwiązywanie równań pierwszego stopnia, osiągają lepsze wyniki w innych dziedzinach matematyki i nauk ścisłych.

Jak Rozwiązywać Równania Pierwszego Stopnia?

Istnieje kilka metod rozwiązywania równań pierwszego stopnia. Poniżej przedstawiamy dwie najpopularniejsze:

Metoda Przenoszenia

Metoda przenoszenia polega na izolowaniu niewiadomej (x) po jednej stronie równania. Aby to zrobić, przenosimy wyrazy z jednej strony równania na drugą, zmieniając ich znak. Pamiętaj, że wykonujemy identyczne operacje po obu stronach równania, aby zachować jego równowagę.

Kroki:

Uporządkuj równanie: Zgrupuj wyrazy z x po jednej stronie równania, a wyrazy wolne (liczby) po drugiej stronie.
Przenieś wyrazy: Pamiętaj o zmianie znaku przy przenoszeniu wyrazu na drugą stronę równania.
Uprość: Zredukuj wyrazy podobne po obu stronach równania.
Podziel: Podziel obie strony równania przez współczynnik przy x, aby otrzymać wartość x.

Przykład:

Rozwiąż równanie: 3x + 2 = x - 4

Przenosimy x z prawej strony na lewą: 3x - x + 2 = -4
Przenosimy 2 z lewej strony na prawą: 3x - x = -4 - 2
Upraszczamy: 2x = -6
Dzielimy obie strony przez 2: x = -3

Otrzymaliśmy rozwiązanie: x = -3

Metoda Działań Odwrotnych

Metoda działań odwrotnych polega na wykonywaniu operacji odwrotnych do tych, które są wykonywane na x. Na przykład, jeśli do x jest dodawana liczba, to odejmujemy tę liczbę od obu stron równania. Jeśli x jest mnożone przez liczbę, to dzielimy obie strony równania przez tę liczbę.

Kroki:

Zidentyfikuj działania na x: Zastanów się, jakie operacje są wykonywane na x (dodawanie, odejmowanie, mnożenie, dzielenie).
Wykonaj działania odwrotne: Wykonaj działania odwrotne do tych, które są wykonywane na x, po obu stronach równania.
Uprość: Zredukuj wyrazy podobne po obu stronach równania.

Przykład:

Rozwiąż równanie: x/2 - 1 = 3

Do x/2 jest odejmowane 1. Zatem dodajemy 1 do obu stron: x/2 - 1 + 1 = 3 + 1
Upraszczamy: x/2 = 4
x jest dzielone przez 2. Zatem mnożymy obie strony przez 2: (x/2) * 2 = 4 * 2
Upraszczamy: x = 8

Otrzymaliśmy rozwiązanie: x = 8

Praktyczne Wskazówki i Narzędzia

Ćwicz, ćwicz, ćwicz: Najlepszym sposobem na opanowanie rozwiązywania równań jest regularne ćwiczenie. Rozwiązuj jak najwięcej przykładów, zaczynając od prostych i stopniowo przechodząc do bardziej skomplikowanych.
Używaj kalkulatora: Kalkulator może być pomocny przy wykonywaniu obliczeń, zwłaszcza przy bardziej skomplikowanych równaniach.
Korzystaj z zasobów online: Istnieje wiele stron internetowych i aplikacji, które oferują ćwiczenia, przykłady i wyjaśnienia dotyczące rozwiązywania równań. Na przykład, strony takie jak Khan Academy (https://www.khanacademy.org/) oferują darmowe materiały edukacyjne.
Szukaj pomocy: Jeśli masz trudności z rozwiązywaniem równań, nie wahaj się poprosić o pomoc nauczyciela, korepetytora lub kolegę.
Sprawdzaj swoje rozwiązania: Po rozwiązaniu równania, zawsze sprawdzaj, czy otrzymane rozwiązanie jest poprawne. Wstaw otrzymaną wartość x do oryginalnego równania i sprawdź, czy obie strony równania są równe.

Pamiętaj, że każdy, nawet najlepsi matematycy, kiedyś zaczynał od podstaw. Nie zrażaj się trudnościami i ciesz się z każdego sukcesu! Jak powiedział słynny matematyk Benoît Mandelbrot: "Matematyka jest wszędzie wokół nas." Zrozumienie równań pierwszego stopnia to pierwszy krok do odkrycia tego piękna.