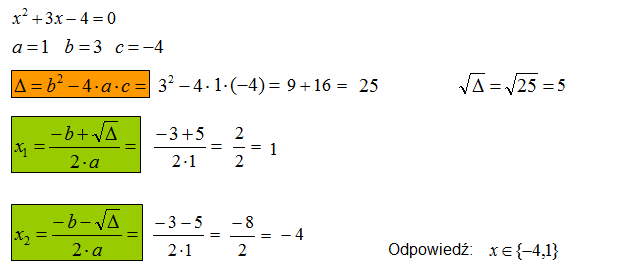Równania I Nierówności Kwadratowe Z Parametrem

Cześć! W tym przewodniku zajmiemy się równaniami i nierównościami kwadratowymi z parametrem. Zacznijmy od podstaw.
Czym właściwie są równania i nierówności kwadratowe z parametrem? To równania i nierówności, które oprócz niewiadomej (zwykle oznaczanej jako 'x') zawierają dodatkową literę – parametr (zazwyczaj oznaczany jako 'm', 'p', 'a' itp.). Parametr to liczba, której wartość wpływa na rozwiązanie równania lub nierówności. Inaczej mówiąc, zmieniając wartość parametru, zmieniamy postać równania/nierówności, a co za tym idzie, jego rozwiązania.
Ogólna postać równania kwadratowego z parametrem to: ax2 + bx + c = 0, gdzie a, b i c to wyrażenia zawierające parametr. Podobnie, nierówność kwadratowa z parametrem ma postać: ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0 lub ax2 + bx + c ≤ 0, gdzie a, b i c znowu zawierają parametr.
Kluczowe idee przy rozwiązywaniu:
- Delta (Δ): Obliczamy deltę, tak jak w zwykłym równaniu kwadratowym: Δ = b2 - 4ac. Uwaga! Delta będzie wyrażeniem zawierającym parametr.
- Analiza delty: W zależności od wartości parametru, delta może być dodatnia, ujemna lub równa zero. To determinuje liczbę rozwiązań równania.
- Δ > 0: Równanie ma dwa różne rozwiązania.
- Δ = 0: Równanie ma jedno rozwiązanie (pierwiastek podwójny).
- Δ < 0: Równanie nie ma rozwiązań rzeczywistych.
- Rozwiązania (pierwiastki): Jeśli Δ ≥ 0, obliczamy pierwiastki równania: x1 = (-b - √Δ) / 2a i x2 = (-b + √Δ) / 2a. Pierwiastki również będą wyrażeniami zawierającymi parametr.
- Analiza rozwiązań: Po obliczeniu rozwiązań, musimy przeanalizować, jak zmieniają się one w zależności od wartości parametru. Może być konieczne wyznaczenie przedziałów, w których rozwiązania spełniają określone warunki (np. oba rozwiązania są dodatnie, jedno rozwiązanie jest większe od 2, itp.).
Przykład: Rozwiąż równanie x2 + 2mx + m2 - 1 = 0 ze względu na liczbę rozwiązań w zależności od wartości parametru m.
Δ = (2m)2 - 4 * 1 * (m2 - 1) = 4m2 - 4m2 + 4 = 4
Ponieważ Δ = 4 > 0 dla każdego m, równanie ma zawsze dwa różne rozwiązania dla dowolnej wartości parametru m.
Nierówności: Rozwiązywanie nierówności kwadratowych z parametrem polega na znalezieniu przedziałów, w których funkcja kwadratowa przyjmuje wartości dodatnie lub ujemne. Po znalezieniu pierwiastków, rysujemy wykres funkcji i analizujemy jego przebieg w zależności od parametru. Pamiętajmy o uwzględnieniu znaku współczynnika 'a' przy x2, który determinuje kierunek ramion paraboli.
Praktyczne zastosowania: Równania i nierówności kwadratowe z parametrem pojawiają się w różnych dziedzinach, na przykład w fizyce (obliczanie toru lotu pocisku), ekonomii (modelowanie kosztów i zysków), informatyce (optymalizacja algorytmów) i inżynierii (projektowanie konstrukcji). Rozwiązywanie tych równań pozwala na analizę i przewidywanie zachowania systemów w zależności od zmieniających się warunków.