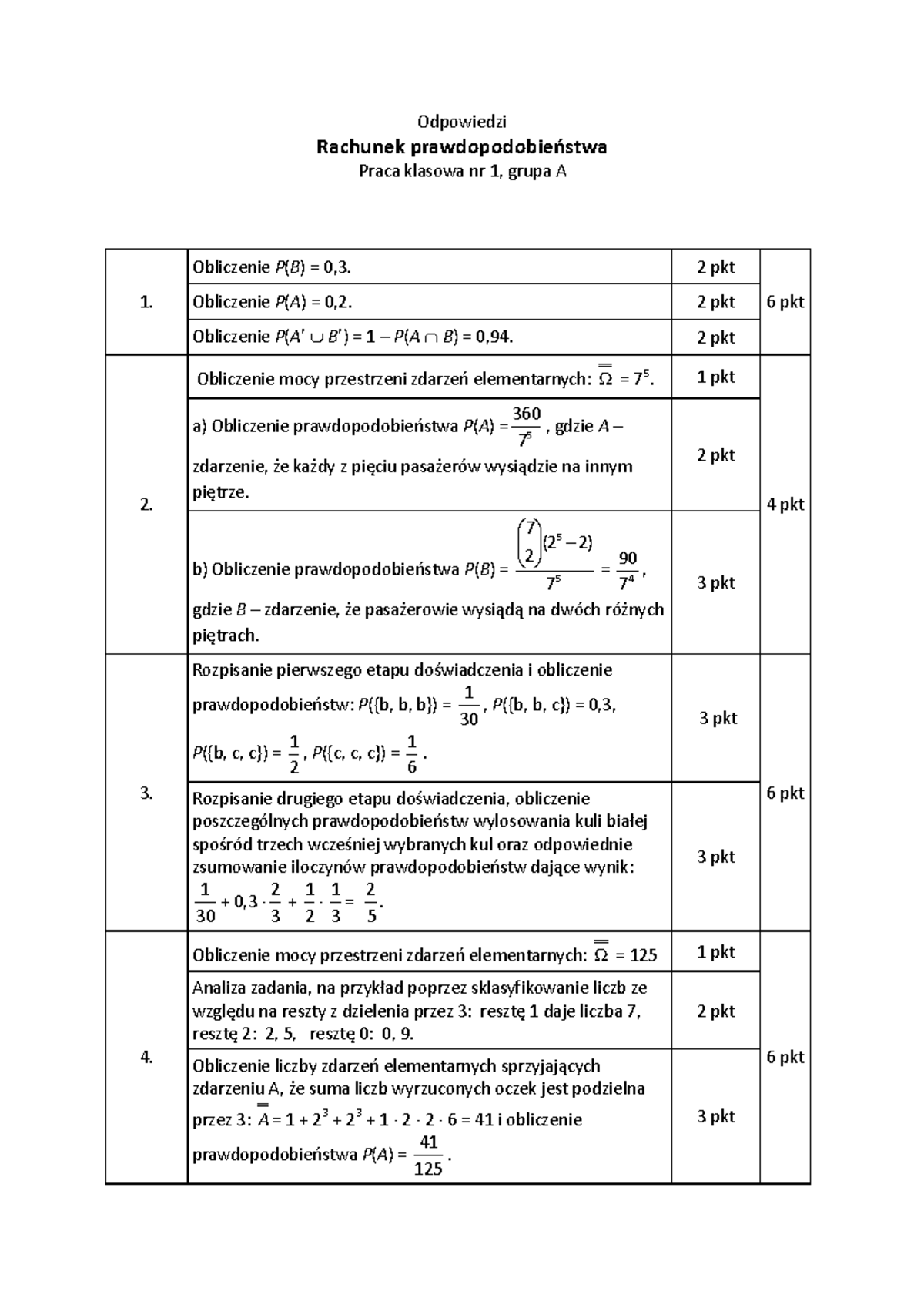
Rachunek Prawdopodobieństwa Sprawdzian Nowa Era 2014 Odpowiedzi

Rozumiemy, jak stresujący może być sprawdzian z rachunku prawdopodobieństwa, zwłaszcza jeśli chodzi o materiał z podręczników Nowej Ery z 2014 roku. To normalne, że czujesz presję, żeby wypaść jak najlepiej. Przygotowanie się do takiego sprawdzianu wymaga nie tylko nauki teorii, ale i praktycznego zastosowania wiedzy. Ten artykuł ma na celu pomóc Ci zrozumieć ten dział matematyki, pokazać, jak się do niego przygotować, i dać Ci pewność siebie przed testem.

Dlaczego Rachunek Prawdopodobieństwa Sprawia Trudności?

Rachunek prawdopodobieństwa często sprawia trudności, ponieważ jest to dział matematyki, który łączy abstrakcyjne koncepcje z realnymi sytuacjami. W przeciwieństwie do algebry, gdzie operujemy na konkretnych liczbach i wzorach, tutaj musimy operować na szansach i możliwościach. Często uczniowie mają problem z:

• Zrozumieniem definicji: czym jest zdarzenie elementarne, przestrzeń zdarzeń, prawdopodobieństwo warunkowe?
• Rozróżnianiem wzorów: kiedy stosować wzór na prawdopodobieństwo sumy, a kiedy na iloczyn zdarzeń?
• Interpretacją zadań: jak przełożyć treść zadania na język matematyki i jakie obliczenia wykonać?
• Brak praktyki: sama teoria to za mało. Trzeba rozwiązywać dużo zadań, aby utrwalić wiedzę.

Pamiętaj, że nie jesteś sam. Wielu uczniów ma podobne problemy. Kluczem do sukcesu jest systematyczna praca i zrozumienie podstawowych pojęć.

Kluczowe Koncepcje z Rachunku Prawdopodobieństwa (Nowa Era 2014)

Zanim przejdziemy do przykładów i strategii, przypomnijmy sobie najważniejsze pojęcia, które mogły pojawić się na sprawdzianie z 2014 roku:

Przestrzeń Zdarzeń Elementarnych (Ω)

To zbiór wszystkich możliwych wyników danego doświadczenia losowego. Na przykład, jeśli rzucamy monetą, Ω = {orzeł, reszka}. Jeśli rzucamy kostką, Ω = {1, 2, 3, 4, 5, 6}. Bardzo ważne jest poprawne określenie przestrzeni zdarzeń w danym zadaniu, ponieważ od tego zależą dalsze obliczenia.

Zdarzenia

Zdarzenie to podzbiór przestrzeni zdarzeń elementarnych. Na przykład, w rzucie kostką, zdarzeniem "wypadła parzysta liczba oczek" jest zbiór {2, 4, 6}. Rozróżniamy zdarzenia pewne (które zawsze zajdą), niemożliwe (które nigdy nie zajdą) i elementarne (zawierające tylko jeden element z przestrzeni zdarzeń).

Prawdopodobieństwo

Prawdopodobieństwo zdarzenia A, oznaczane jako P(A), to liczba z przedziału [0, 1], która określa szansę zajścia tego zdarzenia. Klasyczna definicja prawdopodobieństwa (często stosowana w zadaniach) mówi, że P(A) = (liczba zdarzeń sprzyjających A) / (liczba wszystkich możliwych zdarzeń elementarnych), pod warunkiem, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne.

Działania na Zdarzeniach

Tutaj wchodzą suma, iloczyn i różnica zdarzeń. Suma zdarzeń A i B (A∪B) zachodzi, gdy zajdzie co najmniej jedno z tych zdarzeń. Iloczyn zdarzeń A i B (A∩B) zachodzi, gdy zajdą oba zdarzenia jednocześnie. Ważne są również zdarzenia wykluczające się (rozłączne), których iloczyn jest zbiorem pustym.

Prawdopodobieństwo Warunkowe

Oznacza prawdopodobieństwo zajścia zdarzenia A, pod warunkiem że zaszło zdarzenie B. Oznacza się je P(A|B) i oblicza ze wzoru P(A|B) = P(A∩B) / P(B), o ile P(B) > 0. Prawdopodobieństwo warunkowe jest kluczowe w wielu bardziej zaawansowanych zadaniach.

Schemat Bernoulliego

Opisuje ciąg niezależnych prób, z których każda kończy się sukcesem z prawdopodobieństwem p lub porażką z prawdopodobieństwem 1-p. Pozwala obliczyć prawdopodobieństwo uzyskania dokładnie k sukcesów w n próbach.

Jak Skutecznie Przygotować się do Sprawdzianu?

Oto kilka praktycznych wskazówek, które pomogą Ci w przygotowaniach:

1. Powtórz teorię: Dokładnie przeczytaj podręcznik Nowej Ery z 2014 roku i upewnij się, że rozumiesz wszystkie definicje i wzory. Spróbuj wytłumaczyć te pojęcia komuś innemu – to świetny sposób na sprawdzenie swojej wiedzy.
2. Rozwiąż zadania: To najważniejszy element przygotowań. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz materiał i nabierzesz wprawy. Zacznij od zadań prostych, a następnie przejdź do bardziej złożonych.
3. Skorzystaj z dostępnych zasobów: Oprócz podręcznika, poszukaj dodatkowych materiałów online, takich jak strony internetowe, filmy na YouTube czy interaktywne ćwiczenia. Często można tam znaleźć przykłady rozwiązań krok po kroku.
4. Pracuj w grupie: Wspólna nauka z kolegami i koleżankami może być bardzo efektywna. Możecie sobie nawzajem tłumaczyć trudne zagadnienia i rozwiązywać zadania razem.
5. Symuluj sprawdzian: Spróbuj rozwiązać test z rachunku prawdopodobieństwa w warunkach zbliżonych do tych na sprawdzianie. To pomoże Ci oswoić się ze stresem i nauczyć się zarządzać czasem.
6. Zadbaj o odpoczynek: Nie ucz się do późna w nocy przed sprawdzianem. Wyspany umysł lepiej pracuje. Zjedz lekką kolację i zrelaksuj się.

Przykładowe Zadania i Rozwiązania (Styl Nowa Era 2014)

Przejdźmy teraz do konkretnych przykładów, aby pokazać, jak stosować wiedzę w praktyce:

Zadanie 1

Rzucamy dwa razy symetryczną monetą. Oblicz prawdopodobieństwo, że wypadnie dokładnie jeden orzeł.

Rozwiązanie:

Przestrzeń zdarzeń elementarnych Ω = {OO, OR, RO, RR}, gdzie O oznacza orła, a R reszkę. Zdarzenie A, polegające na wypadnięciu dokładnie jednego orła, to zbiór {OR, RO}. Zatem P(A) = (liczba zdarzeń sprzyjających A) / (liczba wszystkich możliwych zdarzeń elementarnych) = 2/4 = 1/2.

Zadanie 2

W urnie jest 5 kul białych i 3 kule czarne. Losujemy bez zwracania dwie kule. Oblicz prawdopodobieństwo, że wylosujemy dwie kule białe.

Rozwiązanie:

Oznaczmy przez B1 zdarzenie, że wylosowano kulę białą w pierwszym losowaniu, a przez B2 zdarzenie, że wylosowano kulę białą w drugim losowaniu. Szukamy prawdopodobieństwa P(B1∩B2). Zauważ, że P(B1) = 5/8. Prawdopodobieństwo P(B2|B1) (wylosowanie kuli białej w drugim losowaniu, pod warunkiem że w pierwszym losowaniu wylosowano kulę białą) wynosi 4/7. Zatem P(B1∩B2) = P(B1) * P(B2|B1) = (5/8) * (4/7) = 20/56 = 5/14.

Zadanie 3

Rzucamy sześć razy kostką. Oblicz prawdopodobieństwo, że szóstka wypadnie dokładnie dwa razy.

Rozwiązanie:

Jest to przykład schematu Bernoulliego. Prawdopodobieństwo sukcesu (wypadnięcie szóstki) wynosi p = 1/6, a prawdopodobieństwo porażki (nie wypadnięcie szóstki) wynosi q = 5/6. Chcemy obliczyć prawdopodobieństwo uzyskania dokładnie 2 sukcesów w 6 próbach. Zatem P = (6 po 2) * (1/6)^2 * (5/6)^4, gdzie (6 po 2) to symbol Newtona, który wynosi 6! / (2! * 4!) = 15. Zatem P = 15 * (1/36) * (625/1296) = 9375 / 46656 ≈ 0.201.

Dodatkowe Ćwiczenia i Aktywności

Oprócz rozwiązywania zadań z podręcznika, możesz spróbować następujących ćwiczeń:

• Symulacje losowe: Użyj kostki, monet, kart do gry, aby przeprowadzić doświadczenia losowe i obliczać prawdopodobieństwa zdarzeń.
• Analiza danych: Zbierz dane statystyczne (np. wyniki rzutów kostką, preferencje wyborcze) i spróbuj obliczyć prawdopodobieństwa różnych zdarzeń.
• Gry losowe: Zagraj w gry losowe (np. poker, lotto) i spróbuj oszacować swoje szanse na wygraną.
• Aplikacje i strony internetowe: Skorzystaj z interaktywnych aplikacji i stron internetowych, które oferują ćwiczenia i testy z rachunku prawdopodobieństwa.

Rachunek Prawdopodobieństwa w Życiu Codziennym

Może Ci się wydawać, że rachunek prawdopodobieństwa to tylko sucha teoria, ale w rzeczywistości ma on wiele zastosowań w życiu codziennym:

• Prognozowanie pogody: Meteorolodzy używają modeli probabilistycznych do przewidywania pogody.
• Ubezpieczenia: Firmy ubezpieczeniowe obliczają ryzyko różnych zdarzeń i ustalają na tej podstawie wysokość składek.
• Medycyna: Lekarze używają rachunku prawdopodobieństwa do diagnozowania chorób i oceny skuteczności leczenia.
• Finanse: Analitycy finansowi używają rachunku prawdopodobieństwa do prognozowania zmian na rynkach finansowych i zarządzania ryzykiem.
• Marketing: Firmy marketingowe używają rachunku prawdopodobieństwa do przewidywania zachowań konsumentów i optymalizacji kampanii reklamowych.

Zrozumienie podstaw rachunku prawdopodobieństwa pozwala na podejmowanie bardziej świadomych decyzji w wielu aspektach życia.

Podsumowanie i Motywacja

Przygotowanie się do sprawdzianu z rachunku prawdopodobieństwa wymaga systematycznej pracy, zrozumienia teorii i dużo praktyki. Nie zrażaj się trudnościami i pamiętaj, że każdy, kto poświęci odpowiednio dużo czasu i wysiłku, może opanować ten dział matematyki.

Uwierz w siebie i swoją zdolność do nauki. Skorzystaj z naszych wskazówek, rozwiązuj zadania, szukaj pomocy, jeśli jej potrzebujesz, i podejdź do sprawdzianu z pewnością siebie i optymizmem. Trzymamy za Ciebie kciuki!

Pamiętaj, że nauka rachunku prawdopodobieństwa to inwestycja w przyszłość. Nabyte umiejętności przydadzą Ci się nie tylko w szkole, ale i w życiu codziennym. Powodzenia!