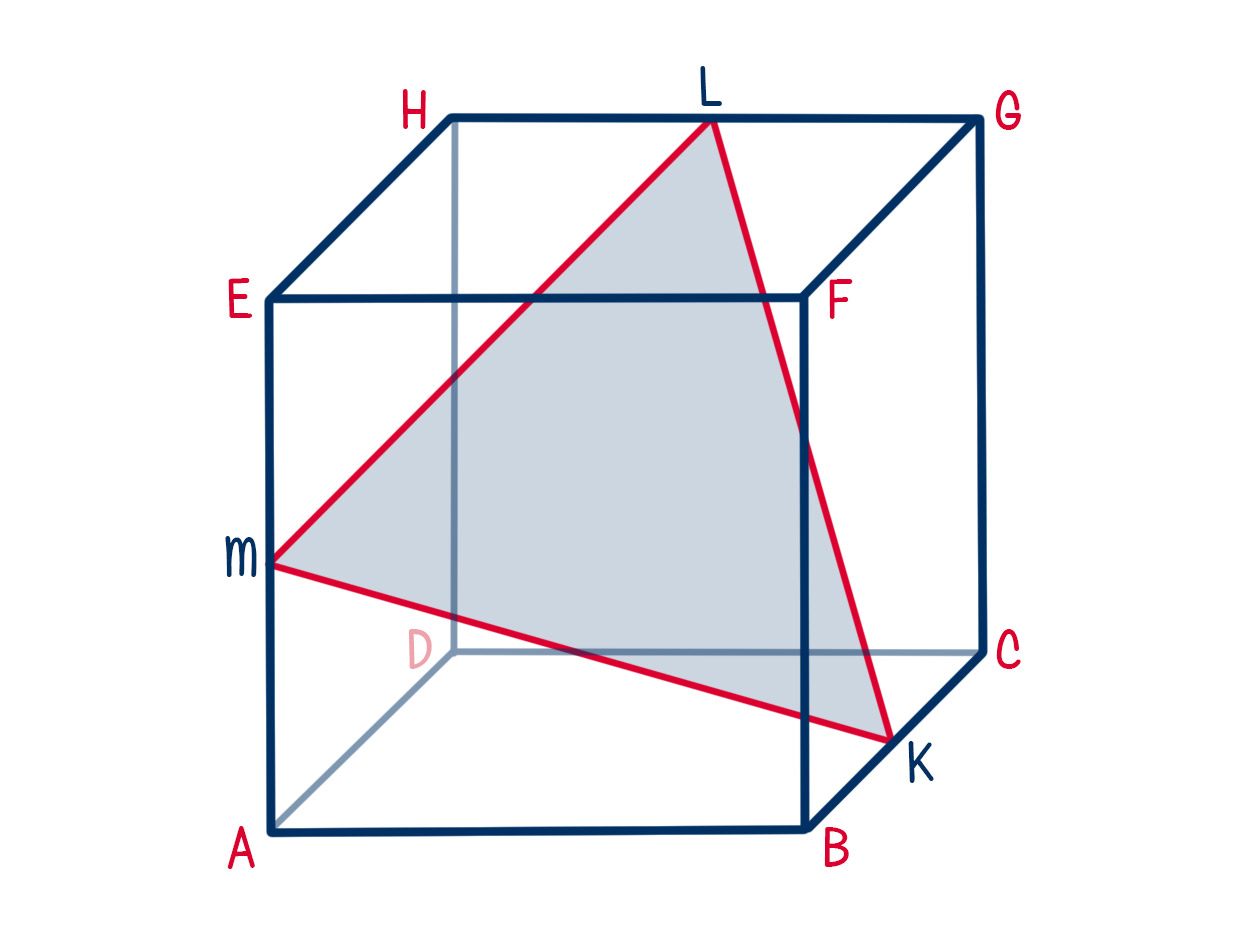
Punkty Klm Są środkami Krawędzi Bc Gh I Ae

Co to jest? Punkty K, L, i M są środkami krawędzi BC, GH i AE w pewnej figurze geometrycznej. To znaczy, punkt K leży dokładnie w połowie długości odcinka BC, punkt L leży dokładnie w połowie długości odcinka GH, a punkt M leży dokładnie w połowie długości odcinka AE. Kluczowe jest słowo środek – oznacza on idealnie podzielenie danego odcinka na dwie równe części.
Jak to działa? Wyobraź sobie sześcian. Krawędź BC to jeden z boków podstawy sześcianu. Znajdź środek tego boku – to jest punkt K. Podobnie, krawędź GH może być jednym z boków górnej podstawy sześcianu. Znajdź środek tego boku – to punkt L. Krawędź AE to jedna z pionowych krawędzi sześcianu. Znajdź środek – to punkt M. To są właśnie te punkty, o których mowa.
Środek odcinka, matematycznie, to punkt, którego współrzędne są średnią arytmetyczną współrzędnych końców odcinka. Jeśli punkt B ma współrzędne (x1, y1, z1) i punkt C ma współrzędne (x2, y2, z2), to punkt K (będący środkiem BC) ma współrzędne ((x1+x2)/2, (y1+y2)/2, (z1+z2)/2). To samo dotyczy punktów L i M, tylko z odpowiednimi współrzędnymi punktów G, H oraz A, E.
Dlaczego to jest ważne? Informacja, że punkty K, L, i M są środkami krawędzi, pozwala nam wykonywać różne obliczenia i dowody geometryczne. Na przykład:
- Obliczanie długości odcinków: Znając współrzędne punktów K, L, i M oraz wierzchołków, możemy obliczyć długość odcinków łączących te punkty.
- Określanie położenia: Znając, że punkt jest środkiem odcinka, możemy wnioskować o jego położeniu względem innych punktów i figur.
- Dowodzenie twierdzeń: Ta informacja może być kluczowa w dowodach geometrycznych dotyczących symetrii, równoległości i innych właściwości figur.
- Konstrukcje geometryczne: Możemy wykorzystać te punkty jako punkty odniesienia do konstruowania innych elementów figury geometrycznej.
Przykład praktyczny: Załóżmy, że chcemy udowodnić, że pewna linia przechodząca przez punkt K jest równoległa do innej linii przechodzącej przez punkt L. Fakt, że K i L są środkami krawędzi, może nam pomóc w wykazaniu, że te linie mają ten sam kierunek, a więc są równoległe.
Podsumowując, świadomość, że punkty K, L i M są środkami krawędzi, dostarcza nam cennej informacji o położeniu tych punktów i ich relacji z innymi elementami figury. Ta informacja jest fundamentalna w wielu zadaniach geometrycznych i pozwala nam na prowadzenie dalszych obliczeń i wniosków.