Postać Ogólna I Kanoniczna Funkcji Kwadratowej

Zastanawiałeś się kiedyś, jak obliczyć optymalną trajektorię lotu piłki do kosza? Albo jak zmaksymalizować zysk ze sprzedaży, biorąc pod uwagę zmieniające się koszty? Odpowiedzi na te i wiele innych pytań kryją się w świecie funkcji kwadratowych! Ten artykuł jest przeznaczony dla uczniów szkół średnich i studentów, którzy chcą zrozumieć, czym są postać ogólna i kanoniczna funkcji kwadratowej, jak je przekształcać i jak wykorzystywać je do rozwiązywania praktycznych problemów.

Wprowadzenie do Funkcji Kwadratowej

Funkcja kwadratowa to funkcja matematyczna, którą można opisać wzorem:

f(x) = ax² + bx + c

Gdzie a, b i c są stałymi, a a jest różne od zera. Graficznym przedstawieniem funkcji kwadratowej jest parabola. To, w jaki sposób ta parabola jest ułożona i jakie ma charakterystyczne punkty (wierzchołek, miejsca zerowe), zależy od wartości współczynników a, b i c.

Dzięki odpowiedniej analizie funkcji kwadratowej możemy rozwiązywać różnorodne problemy, od obliczeń inżynieryjnych po optymalizację procesów biznesowych. Kluczem do sukcesu jest zrozumienie różnych postaci, w jakich możemy zapisać tę funkcję, a mianowicie postaci ogólnej i kanonicznej.

Postać Ogólna Funkcji Kwadratowej

Postać ogólna funkcji kwadratowej, jak już wspomniano, to:

f(x) = ax² + bx + c

Gdzie:

• a, b, i c są współczynnikami liczbowymi.
• a ≠ 0 (inaczej mielibyśmy funkcję liniową).

Współczynniki te mają istotny wpływ na wygląd paraboli:

• a: Określa kierunek otwarcia paraboli. Jeśli a > 0, parabola jest skierowana w górę (uśmiech), a jeśli a < 0, parabola jest skierowana w dół (smutek). Ponadto wartość bezwzględna |a| wpływa na "szerokość" paraboli – im większa |a|, tym parabola jest węższa.
• b: Wraz z a wpływa na położenie wierzchołka paraboli.
• c: Określa punkt przecięcia paraboli z osią y. Inaczej mówiąc, jest to wartość funkcji dla x = 0.

Zalety i Wady Postaci Ogólnej

Zalety:

• Prosta do zapisu: Jest to najprostsza i najbardziej intuicyjna forma zapisu funkcji kwadratowej.
• Łatwe obliczanie wartości funkcji: Wystarczy podstawić wartość x do wzoru.
• Bezpośrednie odczytanie punktu przecięcia z osią Y: Jest to po prostu wartość współczynnika c.

Wady:

• Trudność w odczytaniu wierzchołka: Bezpośrednio z postaci ogólnej nie da się łatwo odczytać współrzędnych wierzchołka paraboli.
• Trudność w identyfikacji przesunięć: Ciężko jest zobaczyć, jak parabola została przesunięta w stosunku do paraboli bazowej y = x².

Postać Kanoniczna Funkcji Kwadratowej

Postać kanoniczna funkcji kwadratowej ma następującą postać:

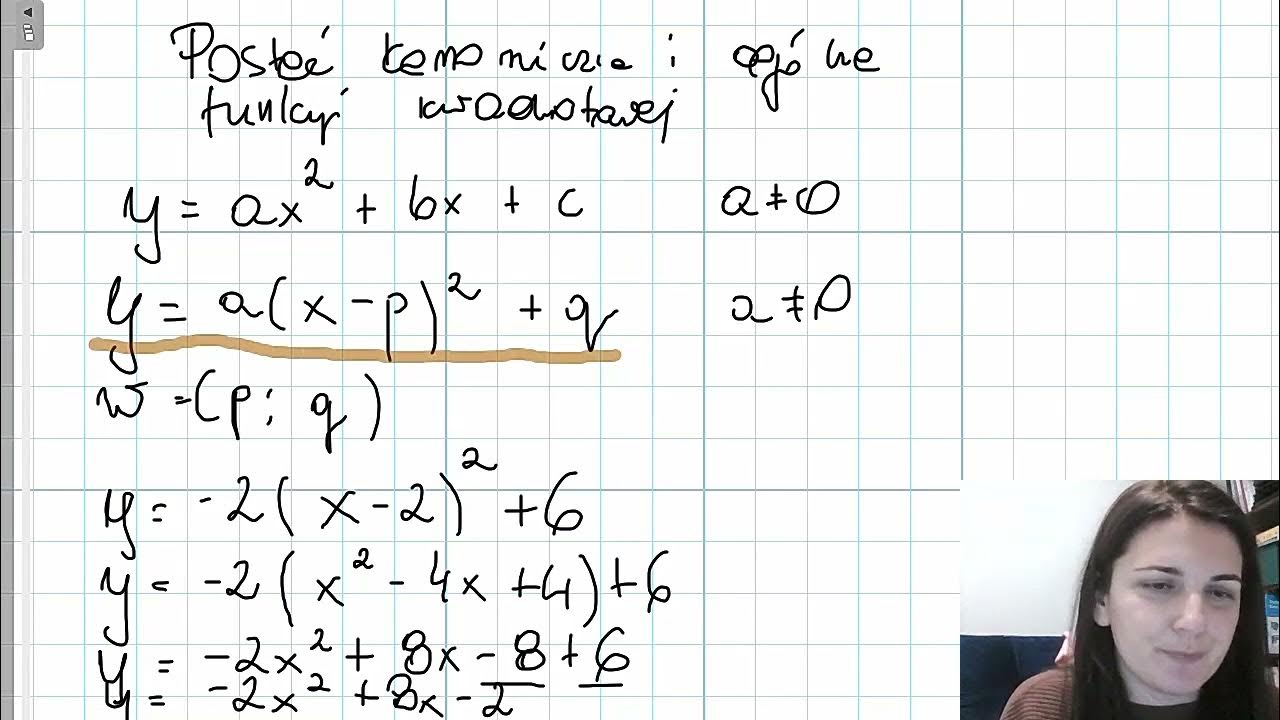
f(x) = a(x - p)² + q

Gdzie:

• a jest tym samym współczynnikiem, co w postaci ogólnej.
• p i q to współrzędne wierzchołka paraboli, czyli W = (p, q).

Postać kanoniczna jest niezwykle przydatna, ponieważ bezpośrednio ujawnia współrzędne wierzchołka paraboli, co ułatwia analizę i rozwiązywanie problemów.

Zalety i Wady Postaci Kanonicznej

Zalety:

• Bezpośredni odczyt wierzchołka: To główna zaleta – współrzędne wierzchołka (p, q) są widoczne od razu.
• Łatwa identyfikacja przesunięć: Można łatwo zobaczyć, jak parabola została przesunięta w poziomie (przez p) i w pionie (przez q) w stosunku do paraboli bazowej y = x².
• Przydatna przy optymalizacji: Pozwala łatwo znaleźć wartość minimalną lub maksymalną funkcji kwadratowej (czyli współrzędną q wierzchołka).

Wady:

• Mniej intuicyjna niż postać ogólna: Może być trudniejsza do zrozumienia na pierwszy rzut oka.
• Trudniejsze obliczanie wartości funkcji bezpośrednio: Wymaga nieco więcej obliczeń niż w postaci ogólnej.
• Trudność w odczytaniu punktu przecięcia z osią Y bezpośrednio: Trzeba wykonać obliczenia (podstawić x = 0).

Przekształcanie Postaci Ogólnej w Kanoniczną i Odwrotnie

Kluczową umiejętnością jest możliwość przekształcania funkcji kwadratowej z postaci ogólnej do kanonicznej i z powrotem. Pozwala to wykorzystywać zalety obu postaci w zależności od potrzeb.

Przekształcanie Postaci Ogólnej w Kanoniczną

Aby przekształcić postać ogólną f(x) = ax² + bx + c w postać kanoniczną f(x) = a(x - p)² + q, należy wykonać następujące kroki:

1. Oblicz p: p = -b / (2a)
2. Oblicz q: q = f(p), czyli podstaw obliczone p do postaci ogólnej funkcji i oblicz wartość. Alternatywnie, możesz obliczyć q jako q = -Δ / (4a), gdzie Δ = b² - 4ac (delta).
3. Podstaw wartości a, p i q do postaci kanonicznej: Otrzymasz f(x) = a(x - p)² + q.

Przykład: Przekształć funkcję f(x) = 2x² + 8x - 3 do postaci kanonicznej.

1. p = -8 / (2 * 2) = -2
2. q = f(-2) = 2*(-2)² + 8*(-2) - 3 = 8 - 16 - 3 = -11
3. Postać kanoniczna: f(x) = 2(x + 2)² - 11

Przekształcanie Postaci Kanonicznej w Ogólną

Aby przekształcić postać kanoniczną f(x) = a(x - p)² + q w postać ogólną f(x) = ax² + bx + c, należy po prostu rozwinąć wzór i uprościć wyrażenie:

1. Rozwiń kwadrat: f(x) = a(x² - 2px + p²) + q
2. Rozмнож: f(x) = ax² - 2apx + ap² + q
3. Zgrupuj wyrazy: f(x) = ax² + (-2ap)x + (ap² + q)
4. Zidentyfikuj współczynniki: Wtedy b = -2ap i c = ap² + q.

Przykład: Przekształć funkcję f(x) = 3(x - 1)² + 5 do postaci ogólnej.

1. Rozwiń kwadrat: f(x) = 3(x² - 2x + 1) + 5
2. Rozмнож: f(x) = 3x² - 6x + 3 + 5
3. Zgrupuj wyrazy: f(x) = 3x² - 6x + 8
4. Postać ogólna: f(x) = 3x² - 6x + 8

Zastosowania Funkcji Kwadratowej

Funkcje kwadratowe mają szerokie zastosowanie w różnych dziedzinach:

• Fizyka: Opisywanie trajektorii rzutów (np. lot piłki, tor pocisku).
• Inżynieria: Projektowanie mostów parabolicznych, anten satelitarnych.
• Ekonomia: Modelowanie kosztów, przychodów i zysków w biznesie, optymalizacja cen.
• Informatyka: Algorytmy grafiki komputerowej, analiza danych.

Przykład 1: Optymalizacja Zysku

Załóżmy, że koszt wyprodukowania x jednostek produktu jest opisany funkcją K(x) = 0.1x² - 2x + 15, a cena sprzedaży jednej jednostki wynosi 5 zł. Jaki poziom produkcji zmaksymalizuje zysk?

Zysk Z(x) to różnica między przychodem (5x) a kosztem: Z(x) = 5x - (0.1x² - 2x + 15) = -0.1x² + 7x - 15. Aby znaleźć maksimum zysku, przekształcamy tę funkcję do postaci kanonicznej:

1. p = -7 / (2 * -0.1) = 35
2. q = Z(35) = -0.1*(35)² + 7*35 - 15 = 107.5
3. Postać kanoniczna: Z(x) = -0.1(x - 35)² + 107.5

Wierzchołek paraboli to (35, 107.5), co oznacza, że maksymalny zysk wynosi 107.5 zł i jest osiągany przy produkcji 35 jednostek.

Przykład 2: Trajektoria Rzutu

Piłka została rzucona pionowo w górę z prędkością początkową 10 m/s. Jej wysokość h(t) (w metrach) po t sekundach jest opisana funkcją h(t) = -5t² + 10t. Jaka jest maksymalna wysokość, jaką osiągnie piłka?

Przekształcamy funkcję do postaci kanonicznej:

1. p = -10 / (2 * -5) = 1
2. q = h(1) = -5*(1)² + 10*1 = 5
3. Postać kanoniczna: h(t) = -5(t - 1)² + 5

Wierzchołek paraboli to (1, 5), co oznacza, że maksymalna wysokość, jaką osiągnie piłka, wynosi 5 metrów i jest osiągana po 1 sekundzie.

Podsumowanie

Zrozumienie postaci ogólnej i kanonicznej funkcji kwadratowej to kluczowa umiejętność w matematyce i jej zastosowaniach. Postać ogólna jest prosta i wygodna do obliczania wartości funkcji, a postać kanoniczna bezpośrednio ujawnia współrzędne wierzchołka, co ułatwia analizę i optymalizację. Umiejętność przekształcania między tymi postaciami pozwala na efektywne rozwiązywanie różnorodnych problemów z życia codziennego i z różnych dziedzin nauki. Ćwicz regularnie przekształcanie funkcji i analizowanie ich właściwości, a przekonasz się, jak potężnym narzędziem jest funkcja kwadratowa!