Postac Kanoniczna I Ogolna Funkcji Kwadratowej

Czy kiedykolwiek patrzyłeś na równanie kwadratowe i czułeś się zagubiony w gąszczu liczb i symboli? Nie jesteś sam! Wielu uczniów, w tym ja kiedyś, zmaga się ze zrozumieniem, jak funkcje kwadratowe faktycznie działają. Profesor John Hattie, znany badacz w dziedzinie edukacji, podkreśla, że "jasne cele i zrozumiałe metody" są kluczem do efektywnej nauki. Dlatego postaramy się rozłożyć funkcję kwadratową na czynniki pierwsze i pokazać, jak przejście między postacią kanoniczną a ogólną może stać się twoim supermocą w matematyce!

Funkcja Kwadratowa - Krótki Wstęp

Funkcja kwadratowa to funkcja, którą można zapisać w postaci:

f(x) = ax² + bx + c

gdzie 'a', 'b' i 'c' są stałymi, a 'a' jest różne od zera. Wykresem funkcji kwadratowej jest parabola. To, jak wygląda ta parabola, zależy od wartości współczynników 'a', 'b' i 'c'.

Dwa kluczowe sposoby zapisu funkcji kwadratowej to postać ogólna i postać kanoniczna. Zrozumienie różnic i połączeń między nimi otwiera drzwi do rozwiązywania wielu problemów.

Postać Ogólna Funkcji Kwadratowej

Jak wspomnieliśmy wcześniej, postać ogólna funkcji kwadratowej wygląda tak:

f(x) = ax² + bx + c

Cechy charakterystyczne:

• Współczynnik 'a' determinuje, czy parabola jest skierowana w górę (a > 0) czy w dół (a < 0). Mówi nam też o "szerokości" paraboli – im większa wartość bezwzględna 'a', tym "węższa" parabola.
• Współczynnik 'c' to punkt przecięcia paraboli z osią Y. To znaczy, że parabola przecina oś Y w punkcie (0, c).
• Wyznaczenie wierzchołka paraboli z postaci ogólnej nie jest od razu widoczne. Wymaga dodatkowych obliczeń.

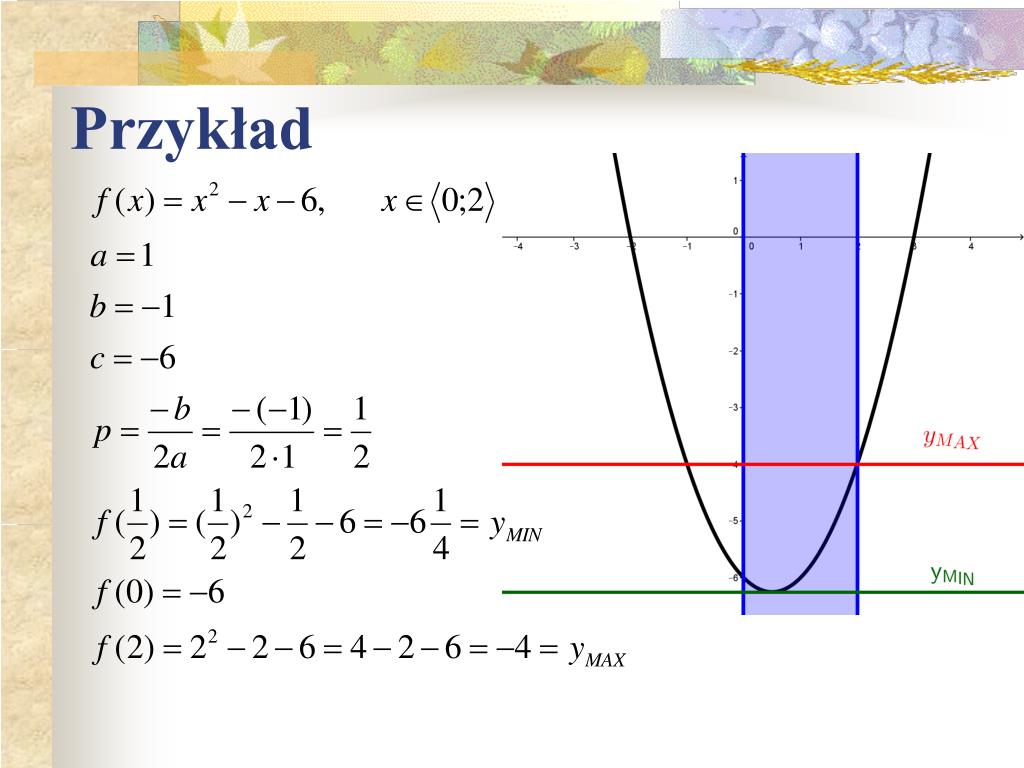
Przykład: f(x) = 2x² - 4x + 1

W tym przykładzie:

• a = 2 (parabola skierowana w górę)
• b = -4
• c = 1 (parabola przecina oś Y w punkcie (0, 1))

Postać Kanoniczna Funkcji Kwadratowej

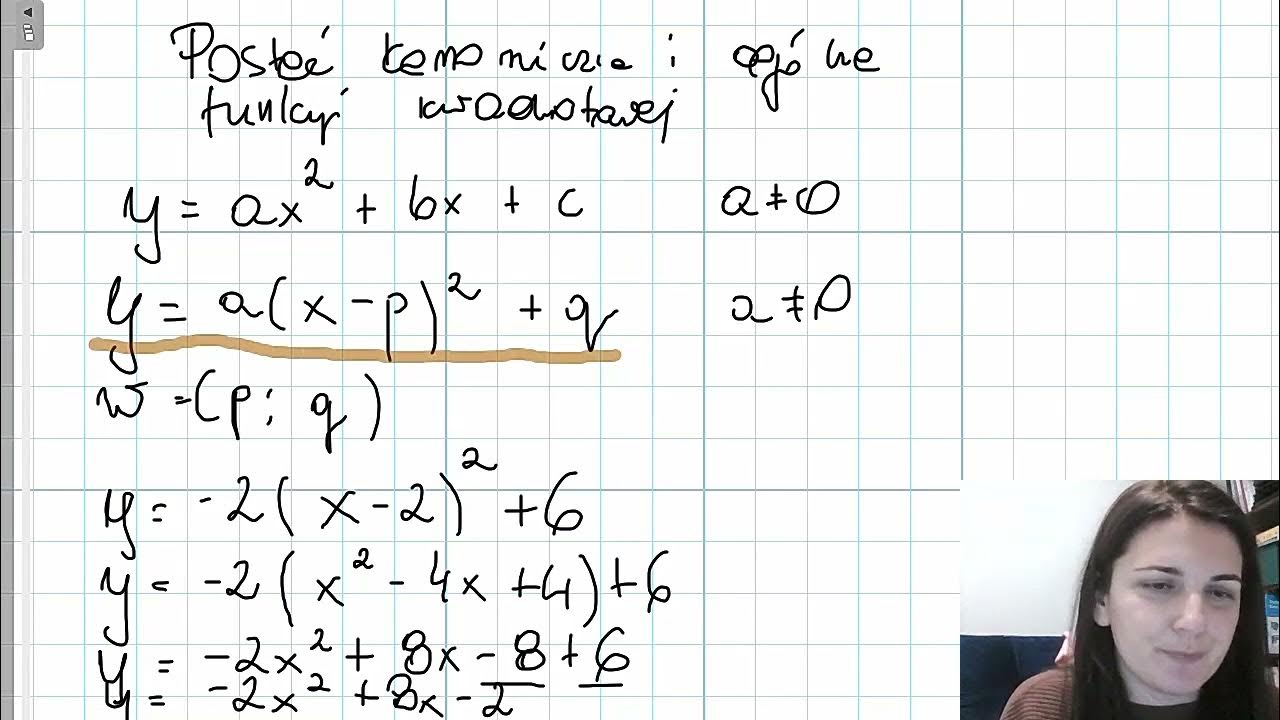
Postać kanoniczna funkcji kwadratowej wygląda następująco:

f(x) = a(x - p)² + q

gdzie:

• 'a' jest tym samym współczynnikiem, co w postaci ogólnej (odpowiada za kierunek i "szerokość" paraboli).
• (p, q) to współrzędne wierzchołka paraboli. To jest kluczowa informacja, którą odczytujemy bezpośrednio z postaci kanonicznej!

Cechy charakterystyczne:

• Wierzchołek paraboli jest od razu widoczny: (p, q).
• Informuje o przesunięciu paraboli bazowej (y = ax²) wzdłuż osi X (przesunięcie o 'p' jednostek) i osi Y (przesunięcie o 'q' jednostek).
• Pozwala łatwo określić wartość najmniejszą (jeśli a > 0) lub wartość największą (jeśli a < 0) funkcji. Wartość ta jest równa 'q'.

Przykład: f(x) = 2(x - 1)² - 1

W tym przykładzie:

• a = 2 (parabola skierowana w górę)
• p = 1
• q = -1
• Wierzchołek paraboli to (1, -1)

Przejście z Postaci Ogólnej do Kanonicznej

Najczęściej używaną metodą przejścia z postaci ogólnej do kanonicznej jest uzupełnianie do pełnego kwadratu. Choć nazwa brzmi skomplikowanie, w praktyce jest to proces, który z odrobiną wprawy staje się intuicyjny.

Kroki:

1. Wyłącz 'a' przed nawias z dwóch pierwszych wyrazów: f(x) = a(x² + (b/a)x) + c
2. Dodaj i odejmij (b/2a)² wewnątrz nawiasu: f(x) = a(x² + (b/a)x + (b/2a)² - (b/2a)²) + c
3. Zwiń wyrażenie w nawiasie do kwadratu różnicy/sumy: f(x) = a((x + b/2a)² - (b/2a)²) + c
4. Przekształć wyrażenie, aby otrzymać postać kanoniczną: f(x) = a(x + b/2a)² - a(b/2a)² + c
   f(x) = a(x - (-b/2a))² + (c - (b²/4a))

Zatem:

• p = -b/2a
• q = c - (b²/4a)

Przykład: Przekształć f(x) = x² - 6x + 5 do postaci kanonicznej.

1. a = 1, więc wyłączamy 1 przed nawias: f(x) = 1(x² - 6x) + 5
2. Dodajemy i odejmujemy (-6/2)² = 9 wewnątrz nawiasu: f(x) = (x² - 6x + 9 - 9) + 5
3. Zwijamy do kwadratu: f(x) = (x - 3)² - 9 + 5
4. Upraszczamy: f(x) = (x - 3)² - 4

Postać kanoniczna to f(x) = (x - 3)² - 4, a wierzchołek paraboli to (3, -4).

Przejście z Postaci Kanonicznej do Ogólnej

Przejście z postaci kanonicznej do ogólnej jest znacznie prostsze. Wystarczy rozwinąć kwadrat i uporządkować wyrazy.

Kroki:

1. Rozwiń (x - p)²: f(x) = a(x² - 2px + p²) + q
2. Pomnóż przez 'a': f(x) = ax² - 2apx + ap² + q
3. Uporządkuj wyrazy: f(x) = ax² + (-2ap)x + (ap² + q)

Zatem:

• b = -2ap
• c = ap² + q

Przykład: Przekształć f(x) = 2(x + 1)² - 3 do postaci ogólnej.

1. Rozwijamy kwadrat: f(x) = 2(x² + 2x + 1) - 3
2. Mnożymy przez 2: f(x) = 2x² + 4x + 2 - 3
3. Upraszczamy: f(x) = 2x² + 4x - 1

Postać ogólna to f(x) = 2x² + 4x - 1.

Dlaczego To Wszystko Ma Znaczenie?

Zrozumienie postaci ogólnej i kanonicznej funkcji kwadratowej jest kluczowe do rozwiązywania różnorodnych problemów. Na przykład:

• Znajdowanie wartości ekstremalnych: Postać kanoniczna od razu pokazuje wierzchołek paraboli, czyli punkt, w którym funkcja osiąga minimum lub maksimum.
• Rysowanie wykresów funkcji kwadratowych: Znając wierzchołek i kierunek paraboli, możemy szybko naszkicować wykres.
• Rozwiązywanie równań kwadratowych: Postać kanoniczna może ułatwić znalezienie miejsc zerowych funkcji, zwłaszcza w przypadkach, gdy postać ogólna jest trudna do rozłożenia na czynniki.
• Optymalizacja: Funkcje kwadratowe często pojawiają się w problemach optymalizacyjnych, gdzie chcemy znaleźć najlepsze rozwiązanie (np. maksymalny zysk, minimalny koszt).

"Matematyka nie jest o liczbach, równaniach, obliczeniach czy algorytmach: chodzi o zrozumienie." - William Paul Thurston, wybitny matematyk.

Narzędzia i Metody Wspierające Naukę

Oto kilka sugestii, które pomogą Ci w opanowaniu tematu:

• Geogebra: Interaktywny program do rysowania wykresów funkcji i eksperymentowania z parametrami. Możesz wpisać funkcję w postaci ogólnej i kanonicznej i zobaczyć, jak zmienia się jej wykres.
• Khan Academy: Darmowe kursy online, w tym lekcje dotyczące funkcji kwadratowych, z przykładami i ćwiczeniami.
• Ćwiczenia, ćwiczenia, ćwiczenia! Rozwiązywanie wielu zadań to najlepszy sposób na utrwalenie wiedzy. Zacznij od prostych przykładów i stopniowo przechodź do bardziej skomplikowanych.
• Stwórz fiszki: Zapisz na nich wzory, definicje i kroki przekształceń. Regularne powtarzanie pomoże Ci zapamiętać najważniejsze informacje.
• Grupowa nauka: Dyskutuj z kolegami, wyjaśniaj sobie nawzajem trudne zagadnienia. Wyjaśnianie komuś to świetny sposób na lepsze zrozumienie tematu.

Podsumowanie

Funkcja kwadratowa w postaci ogólnej i kanonicznej to dwa różne sposoby zapisu tej samej funkcji. Przejście między nimi daje nam różne perspektywy i ułatwia rozwiązywanie różnych problemów. Pamiętaj, że ćwiczenie czyni mistrza. Im więcej będziesz rozwiązywał zadań, tym pewniej będziesz się czuł z funkcjami kwadratowymi. Nie zrażaj się trudnościami – każdy, nawet najtęższy umysł, zaczynał od podstaw. Powodzenia!