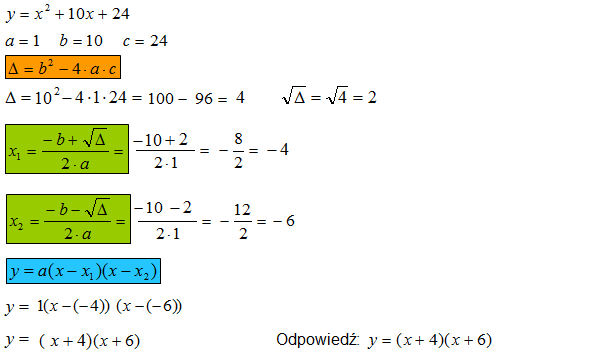Postać Iloczynowa Z Jednym Miejscem Zerowym

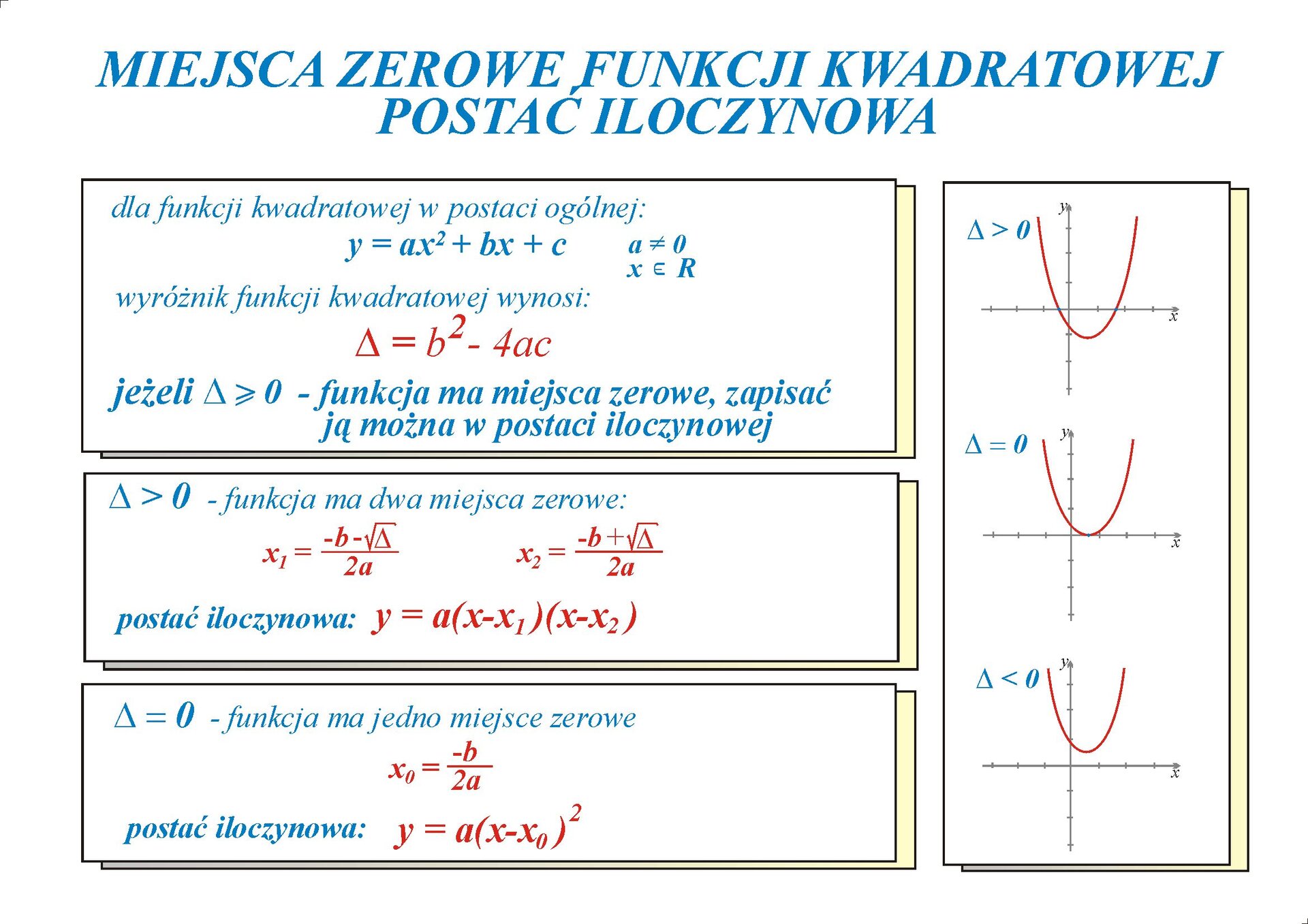
Postać iloczynowa z jednym miejscem zerowym to szczególny przypadek postaci iloczynowej funkcji kwadratowej, w którym funkcja kwadratowa ma jedno, podwójne miejsce zerowe. Oznacza to, że wykres funkcji (parabola) dotyka osi OX tylko w jednym punkcie.
Aby zrozumieć ten koncept krok po kroku, zacznijmy od ogólnej postaci iloczynowej funkcji kwadratowej:
f(x) = a(x - x1)(x - x2)
Gdzie:
- a to współczynnik kierunkowy paraboli (określa czy parabola jest skierowana w górę czy w dół).
- x1 i x2 to miejsca zerowe funkcji.
W przypadku, gdy funkcja ma jedno miejsce zerowe, x1 = x2. Oznaczmy to miejsce zerowe jako x0. Wtedy postać iloczynowa upraszcza się do:
f(x) = a(x - x0)(x - x0)
Lub po uproszczeniu:
f(x) = a(x - x0)2
Oto kilka przykładów, które pomogą to lepiej zrozumieć:
Przykład 1: Znajdź postać iloczynową funkcji kwadratowej, która ma jedno miejsce zerowe x0 = 3 i a = 2.
Rozwiązanie: Podstawiamy wartości do wzoru: f(x) = 2(x - 3)2
Przykład 2: Funkcja f(x) = -1(x + 4)2. Jakie jest jej miejsce zerowe i współczynnik kierunkowy?
Rozwiązanie: Porównując z ogólnym wzorem widzimy, że a = -1 (parabola skierowana w dół), a x0 = -4 (ponieważ (x - (-4)) = (x + 4)).
Przykład 3: Przeprowadź funkcję zapisaną w postaci ogólnej: f(x) = x2 - 6x + 9 do postaci iloczynowej.
Rozwiązanie: Musimy znaleźć miejsce zerowe. Zauważamy, że x2 - 6x + 9 to wzór skróconego mnożenia (x - 3)2. Zatem f(x) = (x - 3)2. Współczynnik a = 1, a miejsce zerowe x0 = 3.
Dlaczego postać iloczynowa z jednym miejscem zerowym jest ważna?
Jednym z praktycznych zastosowań jest znajdowanie wierzchołka paraboli. W przypadku funkcji kwadratowej w tej postaci, wierzchołek paraboli znajduje się w punkcie (x0, 0). Znając wierzchołek, łatwo można naszkicować wykres funkcji i zrozumieć jej zachowanie.
Innym zastosowaniem jest rozwiązywanie zadań optymalizacyjnych. Jeśli funkcja opisuje pewien proces (np. zysk firmy w zależności od ceny produktu), to wierzchołek paraboli (czyli miejsce zerowe w tym szczególnym przypadku) może wskazywać na optymalną wartość parametru (np. cenę, która maksymalizuje zysk).