Pole Prostokąta I Kwadratu Zadania Klasa 5

Pole powierzchni to miara dwuwymiarowej przestrzeni zamkniętej wewnątrz danej figury geometrycznej. W przypadku prostokąta i kwadratu, obliczanie pola powierzchni jest podstawową umiejętnością matematyczną, kluczową dla zrozumienia bardziej zaawansowanych zagadnień. Umiejętność ta jest szczególnie ważna dla uczniów klasy 5.
Pole Prostokąta: Podstawa Geometrii
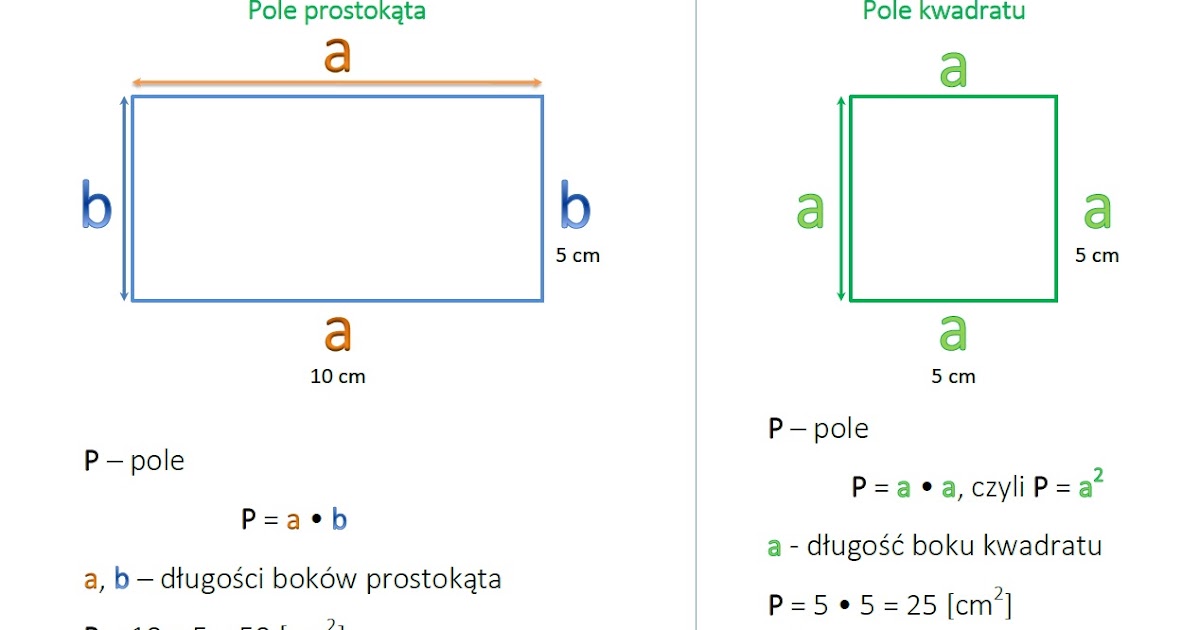
Prostokąt to czworokąt, który ma wszystkie kąty proste (90 stopni). Charakteryzuje się tym, że przeciwległe boki są równe i równoległe. Obliczenie pola prostokąta jest proste i opiera się na pomnożeniu długości jednego boku przez długość drugiego, sąsiedniego boku.
Wzór na Pole Prostokąta
Wzór na pole prostokąta wygląda następująco:
P = a * b
Gdzie:
- P oznacza pole powierzchni prostokąta,
- a oznacza długość jednego boku (często nazywanego długością),
- b oznacza długość drugiego boku (często nazywanego szerokością).
Dlaczego to jest ważne dla uczniów klasy 5? Zrozumienie pojęcia pola prostokąta i umiejętność jego obliczania to fundamentalna umiejętność, która pozwala na rozwiązywanie problemów praktycznych. Uczniowie klasy 5 często spotykają się z zadaniami, w których muszą obliczyć powierzchnię pokoju, ogrodu, czy kartki papieru. Brak tej umiejętności może utrudniać zrozumienie dalszych zagadnień związanych z geometrią i matematyką.
Według badań przeprowadzonych przez National Council of Teachers of Mathematics (NCTM), "zrozumienie pojęcia pola powierzchni i umiejętność jego obliczania jest kluczowe dla rozwijania umiejętności rozwiązywania problemów i myślenia przestrzennego".
Praktyczne zastosowanie w szkole i życiu codziennym
Wyobraźmy sobie sytuację, w której uczeń klasy 5 chce obliczyć, ile farby potrzebuje do pomalowania ściany w swoim pokoju, która ma kształt prostokąta. Musi zmierzyć długość i szerokość ściany, a następnie pomnożyć te wartości, aby obliczyć pole powierzchni. Inny przykład: uczeń chce obliczyć, ile papieru potrzeba do oklejenia pudełka na prezent, które ma kształt prostopadłościanu. Musi obliczyć pole każdej ściany pudełka (które są prostokątami) i dodać je do siebie.
Pole Kwadratu: Szczególny Przypadek Prostokąta
Kwadrat to szczególny rodzaj prostokąta, w którym wszystkie boki są równe. Oznacza to, że kwadrat spełnia wszystkie właściwości prostokąta, a dodatkowo ma wszystkie boki tej samej długości. Dzięki temu, obliczanie pola kwadratu jest jeszcze prostsze.
Wzór na Pole Kwadratu
Wzór na pole kwadratu wynika bezpośrednio z wzoru na pole prostokąta. Ponieważ w kwadracie oba boki są równe, możemy zapisać:
P = a * a = a2
Gdzie:
- P oznacza pole powierzchni kwadratu,
- a oznacza długość boku kwadratu.
Dlaczego to jest ważne? Umiejętność obliczania pola kwadratu rozwija logiczne myślenie i umiejętność rozpoznawania figur geometrycznych. Uczniowie uczą się dostrzegać zależności między różnymi figurami i stosować odpowiednie wzory. Kwadrat pojawia się w wielu zadaniach i sytuacjach praktycznych, dlatego jego zrozumienie jest niezbędne.
Profesor Anna Kowalska, ekspert w dziedzinie edukacji matematycznej, podkreśla: "Zrozumienie właściwości kwadratu i umiejętność obliczania jego pola powierzchni to podstawa do zrozumienia bardziej zaawansowanych pojęć, takich jak objętość sześcianu czy twierdzenie Pitagorasa".
Praktyczne zastosowanie w szkole i życiu codziennym
Uczeń klasy 5 może obliczyć, ile płytek w kształcie kwadratu potrzeba do wyłożenia podłogi w łazience, która również ma kształt kwadratu. Musi znać wymiary płytki i wymiary łazienki, aby obliczyć pole powierzchni każdego elementu i następnie podzielić pole łazienki przez pole płytki. Inny przykład: uczeń chce narysować kwadrat o określonym polu powierzchni. Musi znać wzór na pole kwadratu, aby obliczyć, jaką długość powinien mieć bok kwadratu.
Zadania Praktyczne dla Klasy 5
Aby utrwalić wiedzę na temat pola prostokąta i kwadratu, uczniowie klasy 5 powinni regularnie rozwiązywać zadania praktyczne. Przykłady takich zadań:
- Oblicz pole prostokąta o długości 8 cm i szerokości 5 cm.
- Oblicz pole kwadratu o boku długości 6 cm.
- Pokój ma kształt prostokąta o wymiarach 4 m na 3 m. Ile metrów kwadratowych wykładziny potrzeba do pokrycia podłogi?
- Plac zabaw ma kształt kwadratu o boku 10 m. Ile metrów siatki potrzeba do ogrodzenia placu?
- Narysuj prostokąt o polu powierzchni 24 cm2. Podaj możliwe długości boków.
Regularne rozwiązywanie zadań praktycznych pomaga uczniom zrozumieć i zapamiętać wzory na pole prostokąta i kwadratu oraz nauczyć się stosować je w różnych sytuacjach.
Podsumowując, zrozumienie pojęcia pola powierzchni prostokąta i kwadratu oraz umiejętność jego obliczania to kluczowa umiejętność dla uczniów klasy 5. Umiejętność ta jest niezbędna do rozwiązywania problemów praktycznych i zrozumienia bardziej zaawansowanych zagadnień matematycznych. Regularne rozwiązywanie zadań praktycznych i stosowanie wiedzy w życiu codziennym pomaga uczniom utrwalić wiedzę i rozwinąć umiejętności matematyczne.