Podstawą Ostrosłupa O Wysokości H Jest Kwadrat

Czy kiedykolwiek patrzyliście na piramidę i zastanawialiście się, jak właściwie obliczyć jej objętość? Albo pomagaliście dziecku z zadaniem z matematyki i nagle poczuliście się, jakbyście cofnęli się do swoich szkolnych lat, próbując przypomnieć sobie wzory na bryły? Nie jesteście sami! Stereometria, a zwłaszcza ostrosłupy, mogą być wyzwaniem. Szczególnie, gdy w grę wchodzi ostrosłup, którego podstawą jest kwadrat, a do tego znamy jego wysokość. Ale spokojnie, rozłożymy to na czynniki pierwsze, krok po kroku.

Podstawy, czyli co to w ogóle jest ostrosłup?

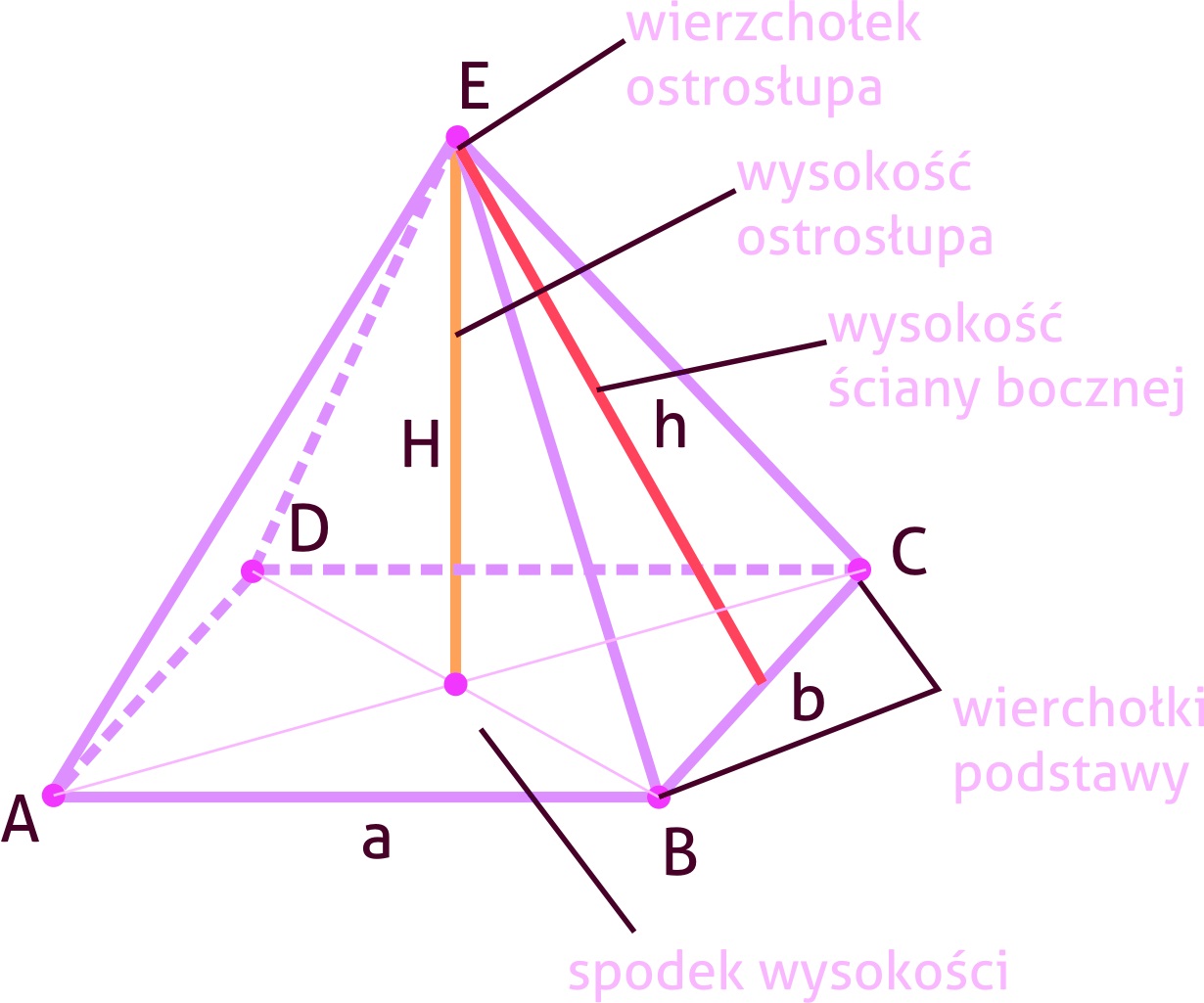
Zacznijmy od definicji. Ostrosłup to bryła, która ma jedną podstawę (w naszym przypadku kwadrat) i jeden wierzchołek, który nie leży w płaszczyźnie podstawy. Wszystkie ściany boczne ostrosłupa są trójkątami, a krawędzie boczne zbiegają się w tym właśnie wierzchołku.

Wyobraź sobie piramidę Cheopsa w Egipcie. Ma ona podstawę w kształcie kwadratu i cztery trójkątne ściany boczne, które łączą się w jednym punkcie na górze. To doskonały przykład ostrosłupa prawidłowego czworokątnego (prawidłowy, bo podstawa jest kwadratem, a wierzchołek jest rzutowany prostopadle na środek podstawy).

No dobrze, ale dlaczego kwadrat w podstawie jest tak ważny? Ano dlatego, że upraszcza nam to obliczenia. Wiemy od razu, jak policzyć pole podstawy, co jest kluczowe do obliczenia objętości ostrosłupa.

Kwadrat jako podstawa – dlaczego to ułatwia sprawę?

Kwadrat to figura, którą znamy i lubimy (a przynajmniej powinniśmy lubić!). Jego najważniejszą cechą jest to, że wszystkie boki są równe. Jeśli oznaczymy długość boku kwadratu jako "a", to pole kwadratu (P_p) obliczymy bardzo prosto:

P_p = a²

Czyli podnosimy długość boku do kwadratu. Koniec! Nie musimy się martwić skomplikowanymi wzorami na pole wielokąta, wszystko jest jasne i proste. To bardzo ważne, ponieważ pole podstawy jest niezbędne do dalszych obliczeń.

Przykład z życia:

Wyobraź sobie, że masz pudełko w kształcie ostrosłupa, którego podstawa to kwadrat o boku 10 cm. Ile papieru ozdobnego potrzebujesz, żeby okleić samą podstawę? Otóż potrzebujesz 10 cm * 10 cm = 100 cm² papieru. Proste, prawda?

Wysokość ostrosłupa – kluczowy parametr

Wysokość ostrosłupa (H) to odcinek, który łączy wierzchołek ostrosłupa z płaszczyzną podstawy i jest do niej prostopadły. Inaczej mówiąc, to najkrótsza droga z czubka piramidy na sam dół.

Wysokość jest kluczowa do obliczenia objętości ostrosłupa. Im wyższy ostrosłup, tym więcej miejsca zajmuje (przy tej samej podstawie). Wyobraź sobie dwa ostrosłupy o identycznych podstawach kwadratowych. Jeden jest niski i spłaszczony, a drugi wysoki i smukły. Oczywiście, ten wyższy ma większą objętość.

Czasami wysokość ostrosłupa jest podana w zadaniu. Innym razem trzeba ją obliczyć, korzystając z innych danych (np. długości krawędzi bocznych i kątów między nimi). To już wymaga odrobinę więcej pracy, ale trzymając się podstawowych zasad geometrii i trygonometrii, na pewno sobie poradzimy!

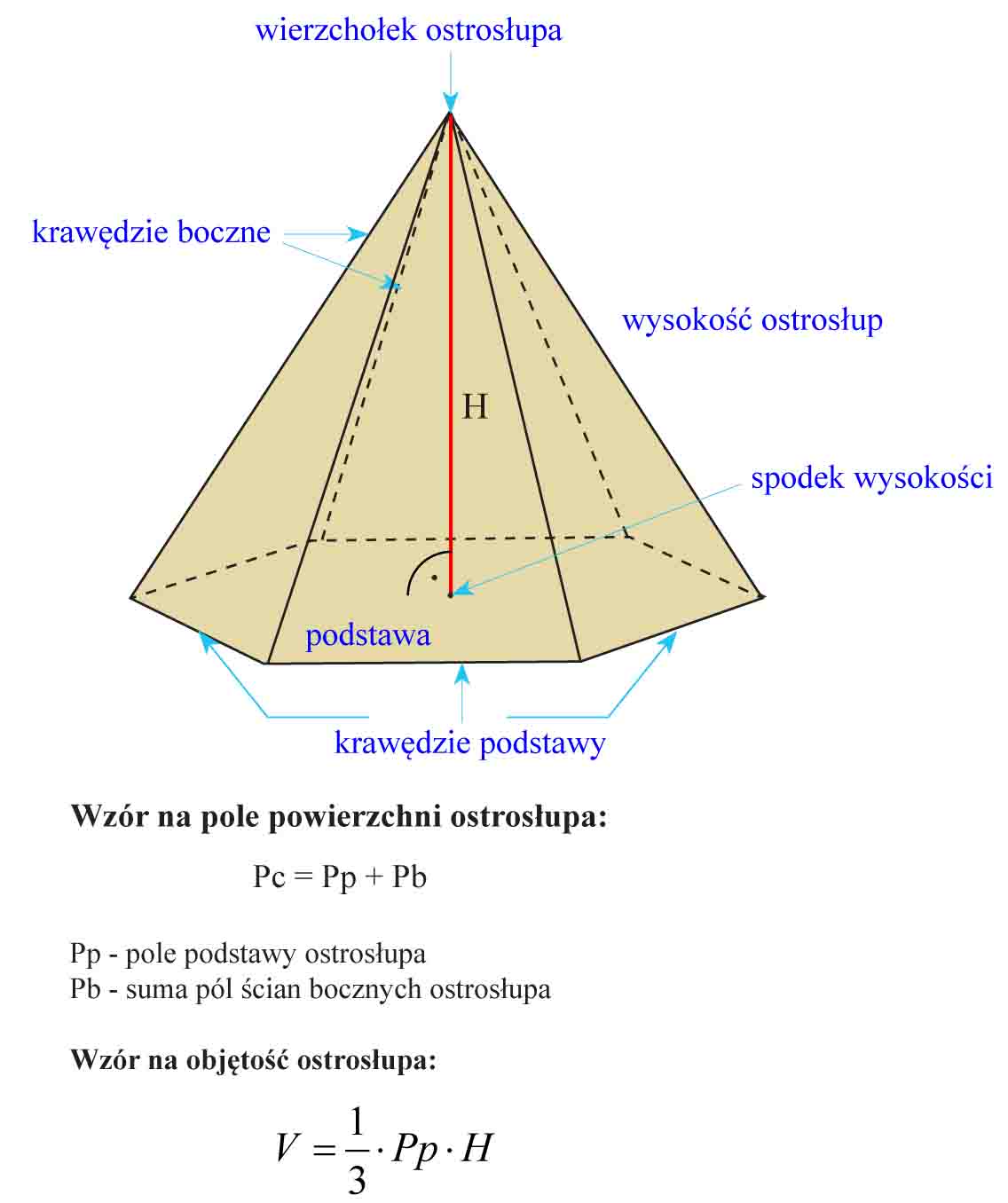
Wzór na objętość ostrosłupa o podstawie kwadratu

Teraz dochodzimy do sedna – wzoru na objętość ostrosłupa o podstawie kwadratu. Jest on stosunkowo prosty i łatwy do zapamiętania:

V = (1/3) * P_p * H

Gdzie:

• V to objętość ostrosłupa
• P_p to pole podstawy (czyli w naszym przypadku pole kwadratu)
• H to wysokość ostrosłupa

Czyli, żeby obliczyć objętość ostrosłupa, musimy wykonać trzy proste kroki:

1. Obliczyć pole kwadratu, który jest podstawą ostrosłupa.
2. Pomnożyć pole podstawy przez wysokość ostrosłupa.
3. Pomnożyć wynik przez 1/3 (albo podzielić przez 3).

To wszystko! Właśnie obliczyliśmy objętość ostrosłupa o podstawie kwadratu!

Przykład obliczeniowy:

Załóżmy, że mamy ostrosłup, którego podstawa jest kwadratem o boku 5 cm, a wysokość ostrosłupa wynosi 8 cm. Jak obliczyć jego objętość?

1. Pole podstawy: P_p = a² = 5 cm * 5 cm = 25 cm²
2. Pomnożenie pola podstawy przez wysokość: 25 cm² * 8 cm = 200 cm³
3. Pomnożenie przez 1/3: (1/3) * 200 cm³ ≈ 66.67 cm³

Odpowiedź: Objętość ostrosłupa wynosi około 66.67 cm³.

Praktyczne zastosowania i ćwiczenia

Wzory to jedno, a praktyka to drugie. Spróbujmy teraz zastosować zdobytą wiedzę w praktyce. Możecie rozwiązywać zadania, które znajdziecie w podręcznikach do matematyki. Możecie też tworzyć własne zadania, wymyślając różne wymiary ostrosłupów.

Zadanie 1: Ostrosłup prawidłowy czworokątny ma krawędź podstawy długości 6 cm, a wysokość 10 cm. Oblicz jego objętość.

Zadanie 2: Objętość ostrosłupa o podstawie kwadratu wynosi 150 cm³, a wysokość 9 cm. Oblicz długość boku kwadratu w podstawie.

Zadanie 3: Zaprojektuj pudełko w kształcie ostrosłupa prawidłowego czworokątnego o określonej objętości (np. 500 cm³). Jakie wymiary (długość boku podstawy i wysokość) musisz wybrać, aby osiągnąć tę objętość?

Rozwiązywanie takich zadań pozwala utrwalić wiedzę i zrozumieć, jak działa wzór na objętość ostrosłupa. Dodatkowo, ćwiczenia w projektowaniu pokazują, jak geometria łączy się z praktycznym zastosowaniem.

Dodatkowe wskazówki i triki

• Pamiętaj o jednostkach! Długość boku kwadratu i wysokość muszą być wyrażone w tej samej jednostce (np. cm), a objętość będzie wtedy wyrażona w jednostce do potęgi trzeciej (np. cm³).
• Zwracaj uwagę na to, czy ostrosłup jest prawidłowy. Jeśli tak, to wysokość pada na środek podstawy, co ułatwia obliczenia.
• W razie wątpliwości, narysuj sobie rysunek pomocniczy. To często pomaga zrozumieć zadanie i zidentyfikować potrzebne dane.
• Nie bój się korzystać z kalkulatora. Skup się na zrozumieniu wzoru i prawidłowym podstawianiu wartości, a obliczenia możesz zostawić kalkulatorowi.

Podsumowanie

Obliczanie objętości ostrosłupa o podstawie kwadratu i znanej wysokości wcale nie musi być trudne. Wystarczy zrozumieć podstawowe definicje, zapamiętać wzór na pole kwadratu i wzór na objętość ostrosłupa, a następnie poćwiczyć rozwiązywanie zadań. Pamiętajcie, że praktyka czyni mistrza!

Mam nadzieję, że ten artykuł rozwiał Wasze wątpliwości i sprawił, że ostrosłupy przestały być straszne. Powodzenia w rozwiązywaniu zadań z geometrii!