Ostrosłupy Sprawdzian 2 Gimnazjum I Odpowiedzi

Ostrosłupy to fascynujące bryły geometryczne, które stanowią ważny element edukacji matematycznej na poziomie gimnazjum. Zrozumienie ich definicji, właściwości i sposobów obliczania podstawowych parametrów, takich jak objętość czy pole powierzchni, jest kluczowe dla dalszego rozwoju w tej dziedzinie. Sprawdzian z ostrosłupów dla drugiego etapu gimnazjum to nie tylko test wiedzy, ale również okazja do utrwalenia i zastosowania zdobytych umiejętności.

Czym są ostrosłupy i dlaczego są ważne w nauczaniu gimnazjalnym?

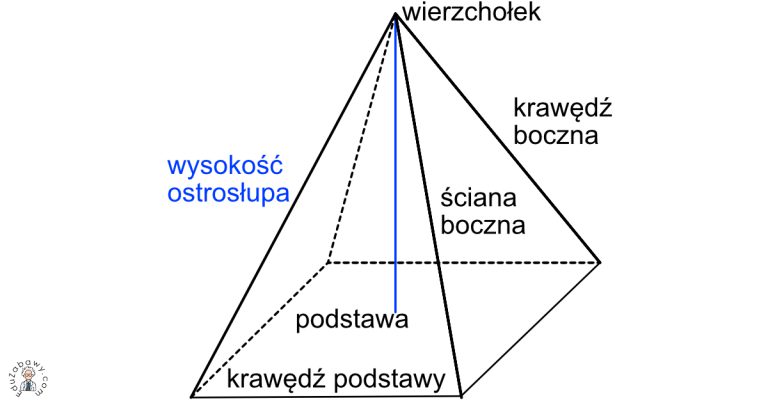
W swej istocie, ostrosłup to wielościan, który ma jedną ścianę nazywaną podstawą, będącą dowolnym wielokątem, oraz ściany boczne, które są trójkątami mającymi wspólny wierzchołek, zwany wierzchołkiem ostrosłupa. Ten wspólny wierzchołek nie leży w płaszczyźnie podstawy.

Znaczenie ostrosłupów w programie nauczania drugiego gimnazjum wynika z kilku kluczowych aspektów:

Rozwój myślenia przestrzennego: Analiza ostrosłupów wymaga od uczniów wizualizacji i manipulacji obiektami w przestrzeni trójwymiarowej. To umiejętność niezbędna nie tylko w matematyce, ale także w wielu innych dziedzinach nauki i życia, jak np. architektura, inżynieria czy projektowanie.
Utrwalenie podstawowych pojęć geometrycznych: Zagadnienia związane z ostrosłupami wykorzystują i pogłębiają wiedzę o wielokątach (podstawy), trójkątach (ściany boczne), liniach prostych (krawędzie, wysokości) i płaszczyznach (ściany, przekroje).
Wprowadzenie do bardziej zaawansowanych brył: Ostrosłupy stanowią fundament do zrozumienia innych, bardziej skomplikowanych brył obrotowych i wielościanów, które pojawiają się w dalszej edukacji.
Budowanie umiejętności rozwiązywania problemów: Zadania sprawdzające wiedzę o ostrosłupach często wymagają zastosowania twierdzenia Pitagorasa, trygonometrii, a także formułowania i rozwiązywania równań.

Według ekspertów, takich jak dr hab. Anna Dudzinska z Uniwersytetu Warszawskiego, specjalistka w dziedzinie dydaktyki matematyki,:

"Kształcenie umiejętności geometrycznych na poziomie gimnazjalnym, w tym poprzez pracę z ostrosłupami, ma fundamentalne znaczenie dla budowania solidnych podstaw teoretycznych i praktycznych dla przyszłych wyzwań edukacyjnych i zawodowych uczniów."

Właściwe opanowanie materiału o ostrosłupach przekłada się bezpośrednio na pewność siebie uczniów w rozwiązywaniu zadań geometrycznych, co jest często wskazywane jako obszar, w którym wielu młodych ludzi napotyka trudności.

Struktura sprawdzianu i kluczowe zagadnienia

Sprawdzian z ostrosłupów dla drugiego gimnazjum zazwyczaj obejmuje następujące zagadnienia:

1. Definicja i rodzaje ostrosłupów

Uczniowie powinni umieć zidentyfikować ostrosłup, podać definicję podstawy, wierzchołka, krawędzi, ścian bocznych i wysokości. Kluczowe jest rozróżnienie:

Ostrosłupy proste: których spodek wysokości pokrywa się ze środkiem okręgu opisanego na podstawie.
Ostrosłupy prawidłowe: które są ostrosłupami prostymi, a ich podstawą jest wielokąt foremny. W ostrosłupach prawidłowych ściany boczne są przystającymi trójkątami równoramiennymi.

Znajomość tych definicji jest pierwszym krokiem do poprawnego rozwiązania zadań.

2. Obliczanie pól powierzchni

Polę powierzchni ostrosłupa stanowi suma pola jego podstawy i pól wszystkich ścian bocznych. Dla ostrosłupów prawidłowych, gdzie wszystkie ściany boczne są przystającymi trójkątami, obliczenie pola powierzchni jest uproszczone:

P_c = P_p + P_b

gdzie:

P_c to pole powierzchni całkowitej.
P_p to pole podstawy.
P_b to pole powierzchni bocznej (suma pól ścian bocznych).

Szczególnie ważna jest umiejętność obliczenia pola jednej ściany bocznej, a następnie pomnożenie jej przez liczbę ścian. Często wymaga to obliczenia wysokości ściany bocznej (zwanej też apotemą ostrosłupa), wykorzystując twierdzenie Pitagorasa.

3. Obliczanie objętości

Objętość każdego ostrosłupa jest równa jednej trzeciej iloczynu pola jego podstawy i wysokości ostrosłupa:

V = (1/3) * P_p * H

gdzie:

V to objętość ostrosłupa.
P_p to pole podstawy.
H to wysokość ostrosłupa (odcinek łączący wierzchołek z płaszczyzną podstawy i prostopadły do niej).

Obliczanie wysokości ostrosłupa jest często najtrudniejszym elementem zadań, wymagającym zastosowania twierdzenia Pitagorasa w przestrzeni, z wykorzystaniem wysokości ostrosłupa, promienia okręgu wpisanego lub opisanego na podstawie oraz apotemy.

Praktyczne zastosowania ostrosłupów w życiu codziennym i nauce

Choć może się wydawać, że ostrosłupy to czysto teoretyczne zagadnienia, mają one liczne odzwierciedlenia w naszym otoczeniu:

Architektura: Najbardziej ikonicznym przykładem są piramidy egipskie, ale również współczesne budowle często wykorzystują kształty ostrosłupów lub ich fragmentów, np. dachy, wieże czy elementy dekoracyjne.
Sztuka i design: Kształt ostrosłupa pojawia się w rzeźbach, elementach biżuterii czy projektach mebli, nadając im nowoczesny i stabilny charakter.
Nauki przyrodnicze: W krystalografii wiele minerałów przyjmuje formy przypominające ostrosłupy.
Przemysł: Leje zasypowe czy niektóre zbiorniki mają kształt ostrosłupów, co ułatwia przepływ materiałów sypkich.

Dla ucznia gimnazjum, zrozumienie ostrosłupów nie jest jedynie ćwiczeniem intelektualnym, ale także wprowadzeniem do świata, w którym matematyka ma konkretne, namacalne zastosowania. Sprawdzian z ostrosłupów, wraz z przykładami i zadaniami, ma na celu utrwalenie tych powiązań i pokazanie, że nauka matematyki jest wartościowa i praktyczna.

Przygotowanie do sprawdzianu: kluczowe wskazówki i możliwe odpowiedzi

Skuteczne przygotowanie do sprawdzianu z ostrosłupów wymaga systematyczności i zrozumienia kluczowych zależności. Uczniowie powinni:

Powtórzyć definicje i wzory: Bez podstawowych definicji i wzorów na pole powierzchni oraz objętość, rozwiązanie zadań jest niemożliwe. Warto mieć je zawsze pod ręką i starać się zapamiętać.
Ćwiczyć rozwiązywanie zadań: Rozwiązywanie różnorodnych zadań, od prostych obliczeń po bardziej złożone problemy wymagające analizy przestrzennej, jest kluczowe. Szczególną uwagę należy zwrócić na zadania, gdzie potrzebne jest wykorzystanie twierdzenia Pitagorasa.
Analizować przykładowe sprawdziany: Zapoznanie się z typowymi zadaniami, które mogą pojawić się na sprawdzianie, oraz analiza proponowanych odpowiedzi, pozwala lepiej przygotować się do formy i poziomu trudności.
Zadawać pytania: Jeśli uczeń ma wątpliwości, powinien śmiało pytać nauczyciela lub kolegów. Wyjaśnienie niejasności jest znacznie lepsze niż pozostawienie ich nierozwiązanych.

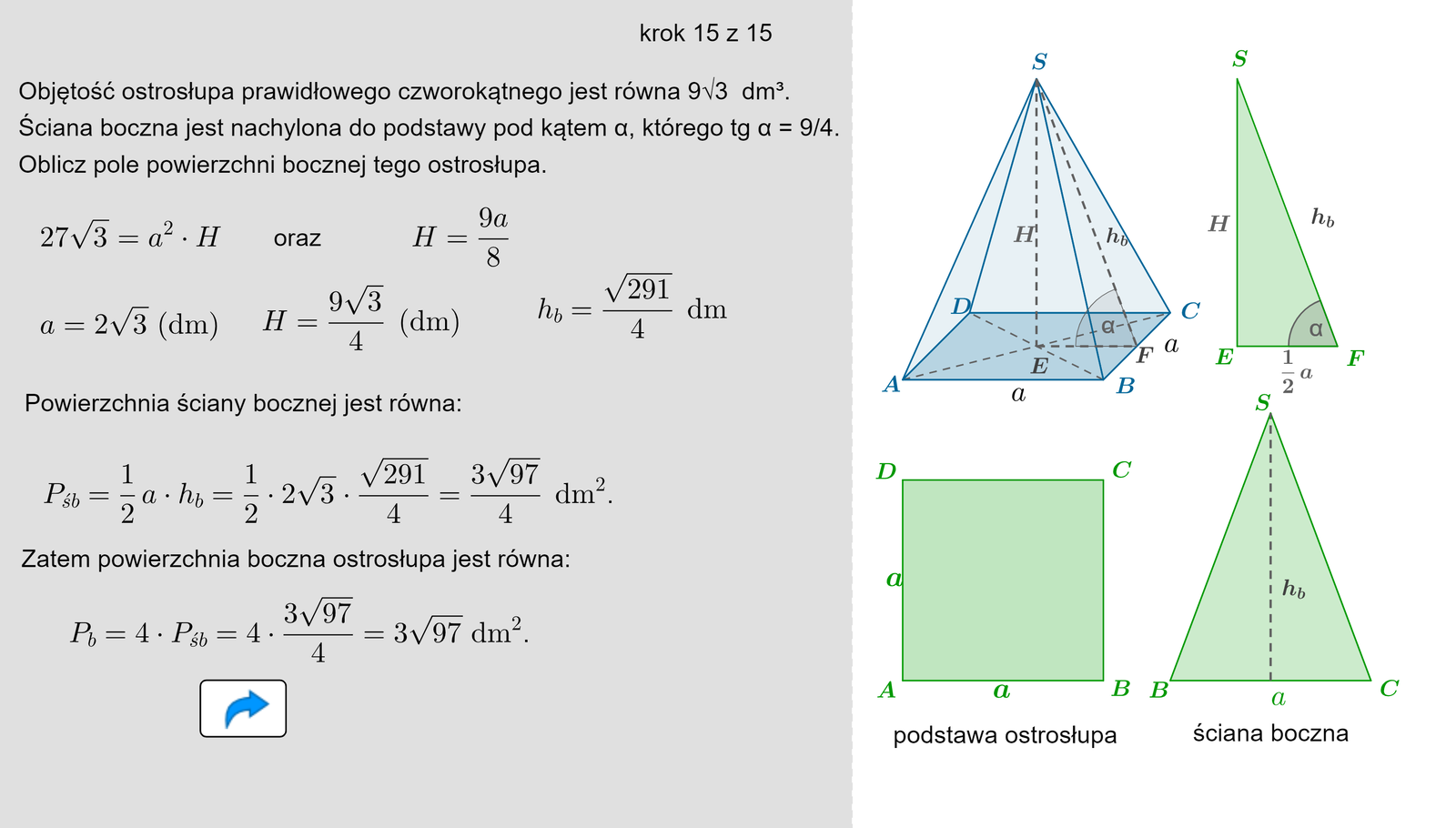
Przykład zadania sprawdzającego umiejętność obliczania objętości ostrosłupa prawidłowego czworokątnego:

Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy równej 6 cm i wysokości ostrosłupa wynoszącej 8 cm. Oblicz objętość tego ostrosłupa.

Odpowiedź:

1. Pole podstawy (kwadratu): $P_p = 6 \text{ cm} * 6 \text{ cm} = 36 \text{ cm}^2$.

2. Objętość: $V = (1/3) * P_p * H = (1/3) * 36 \text{ cm}^2 * 8 \text{ cm} = 12 \text{ cm}^2 * 8 \text{ cm} = 96 \text{ cm}^3$.

Objętość ostrosłupa wynosi 96 cm³.

Podsumowując, ostrosłupy to istotny temat w nauczaniu matematyki w gimnazjum. Sprawdziany z tego zakresu mają na celu weryfikację, czy uczniowie opanowali nie tylko teoretyczne definicje, ale także praktyczne umiejętności ich stosowania w obliczeniach. Właściwe zrozumienie tych brył otwiera drzwi do dalszego, bogatszego poznawania świata geometrii.