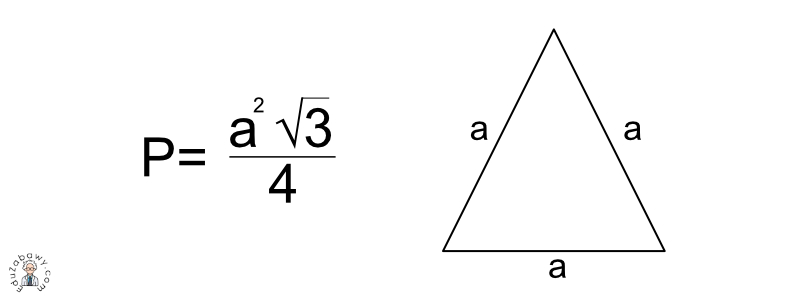Hej! Rozumiem, geometria potrafi czasem sprawić trudności, zwłaszcza kiedy pojawiają się wzory i obliczenia. Ale nie martw się! Dziś wspólnie rozwiążemy problem z trójkątem równobocznym o boku 8 cm. Krok po kroku wytłumaczę, jak obliczyć jego pole. Gwarantuję, że po przeczytaniu tego artykułu, zadanie to wyda Ci się dziecinnie proste!
Dlaczego Trójkąt Równoboczny Jest Wyjątkowy?
Zanim przejdziemy do obliczeń, poświęćmy chwilę na zrozumienie, co sprawia, że trójkąt równoboczny jest tak szczególny. Otóż, wszystkie jego boki są równe, a co za tym idzie, wszystkie kąty wewnętrzne mają miarę 60 stopni. To regularność bardzo ułatwia obliczenia, ponieważ możemy korzystać ze specjalnych wzorów. Pomyśl o nim jak o idealnie symetrycznym i zbalansowanym kształcie – to czyni go wyjątkowym w świecie geometrii!
Co mówią eksperci?
Nauczyciele matematyki często podkreślają, że zrozumienie właściwości figur geometrycznych jest kluczowe do rozwiązywania zadań. Pani Anna Kowalska, nauczycielka z 15-letnim stażem, mówi: "Ważne jest, aby uczeń zrozumiał, dlaczego dany wzór działa, a nie tylko mechanicznie go stosował. To procentuje w przyszłości!". Pamiętajmy o tym!
Wzór na Pole Trójkąta Równobocznego – Nasz Klucz do Sukcesu
Teraz przejdźmy do konkretów. Najprostszym sposobem na obliczenie pola trójkąta równobocznego jest użycie wzoru:
P = (a2 * √3) / 4
Gdzie:
- P to pole trójkąta.
- a to długość boku trójkąta.
- √3 to pierwiastek kwadratowy z 3 (w przybliżeniu 1.732).
Ten wzór wyprowadzany jest z ogólnego wzoru na pole trójkąta (P = 1/2 * a * h), gdzie 'a' to podstawa, a 'h' to wysokość. W trójkącie równobocznym wysokość można obliczyć z twierdzenia Pitagorasa, co prowadzi właśnie do tego uproszczonego wzoru.
Krok po Kroku – Obliczamy Pole Naszego Trójkąta
Skoro znamy już wzór, możemy podstawić do niego dane z naszego zadania. Wiemy, że bok trójkąta (a) ma długość 8 cm.
1. Podstawiamy wartość 'a' do wzoru:
P = (82 * √3) / 4
2. Obliczamy kwadrat długości boku:
P = (64 * √3) / 4
3. Dzielimy wynik przez 4:
P = 16 * √3
4. Przybliżamy wartość √3 (1.732):
P ≈ 16 * 1.732
5. Mnożymy 16 przez 1.732:
P ≈ 27.712 cm2
Odpowiedź: Pole trójkąta równobocznego o boku 8 cm wynosi w przybliżeniu 27.712 cm2.
Alternatywna Metoda – Użycie Wysokości
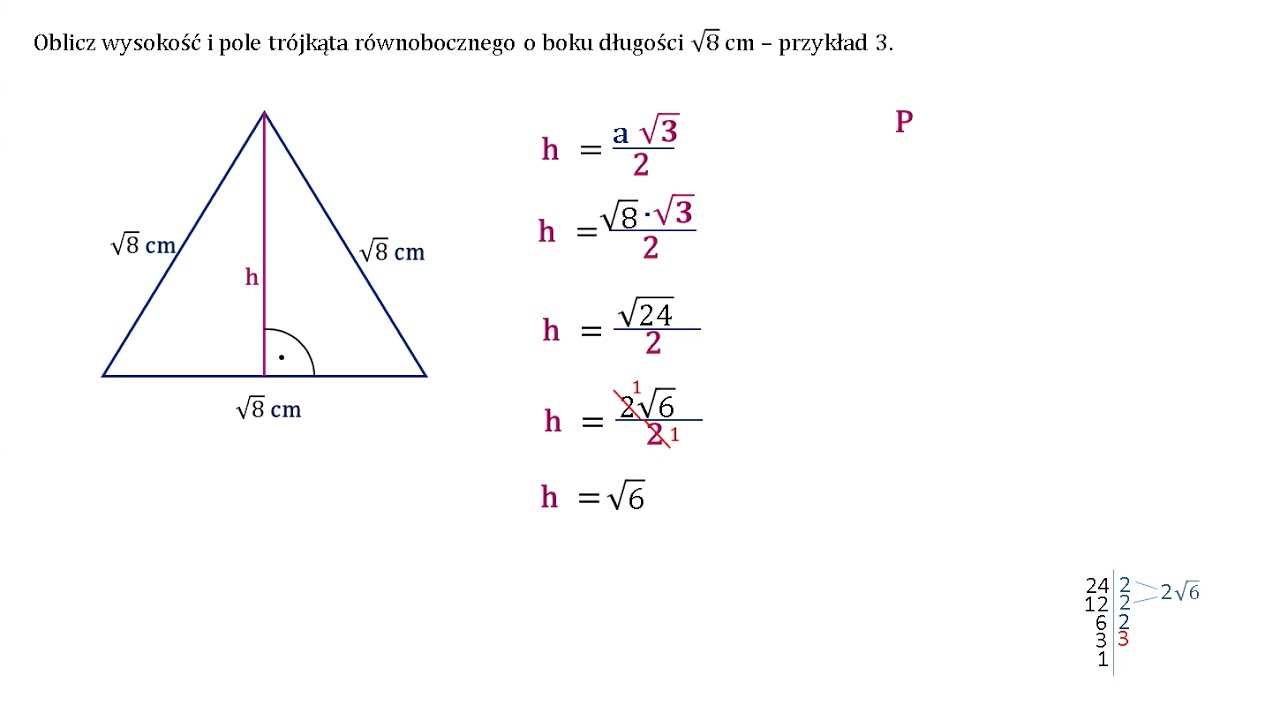
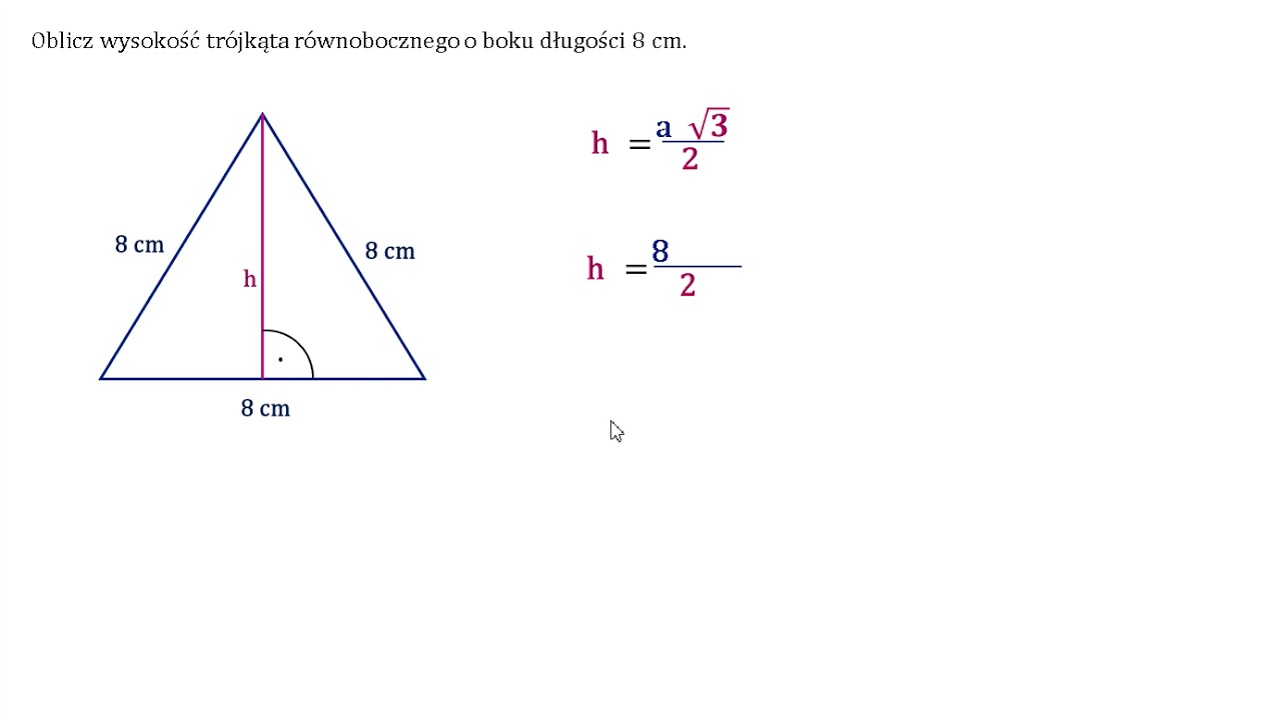
Jeśli wolisz, możesz obliczyć pole trójkąta równobocznego, najpierw obliczając jego wysokość, a następnie korzystając z ogólnego wzoru na pole trójkąta. Jak to zrobić?
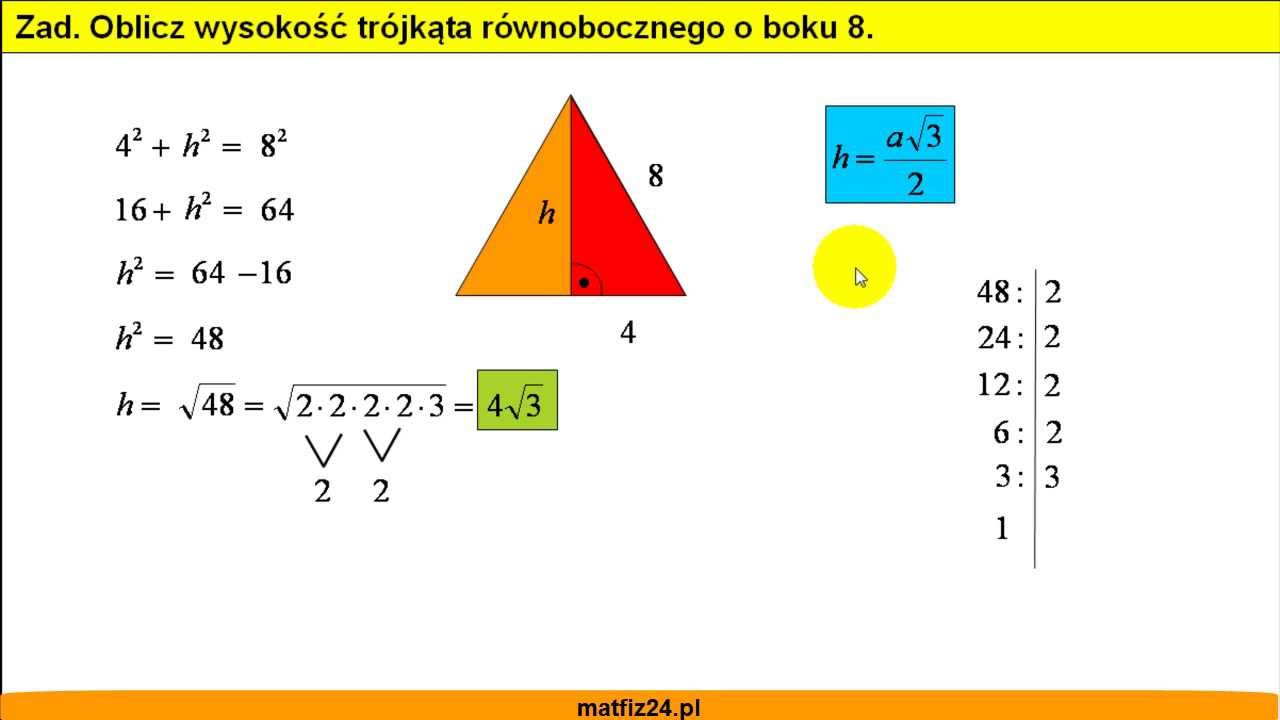
1. Obliczamy wysokość (h): Wysokość w trójkącie równobocznym dzieli go na dwa trójkąty prostokątne. Możemy więc skorzystać z twierdzenia Pitagorasa:
h2 + (a/2)2 = a2
h2 + (8/2)2 = 82
h2 + 42 = 64
h2 + 16 = 64
h2 = 48
h = √48 = √(16 * 3) = 4√3
2. Używamy ogólnego wzoru na pole trójkąta:
P = (1/2) * a * h
P = (1/2) * 8 * 4√3
P = 4 * 4√3
P = 16√3
Jak widzisz, otrzymujemy ten sam wynik! Wybierz metodę, która jest dla Ciebie bardziej zrozumiała.
Praktyczne Ćwiczenia – Utrwalamy Wiedzę!
Teraz czas na trochę praktyki. Spróbuj samodzielnie obliczyć pole trójkątów równobocznych o następujących bokach:
- Trójkąt o boku 5 cm.
- Trójkąt o boku 10 cm.
- Trójkąt o boku 12 cm.
Sprawdź swoje wyniki z kalkulatorem lub poproś kogoś o pomoc. Pamiętaj, że praktyka czyni mistrza!
Zastosowanie w Życiu Codziennym
Może Ci się wydawać, że obliczanie pola trójkąta to czysta teoria, ale wiedza ta przydaje się w wielu sytuacjach. Na przykład, jeśli chcesz obliczyć, ile materiału potrzebujesz do uszycia żagla w kształcie trójkąta, lub ile farby potrzeba do pomalowania trójkątnej ściany. Geometria jest wszędzie wokół nas!
Dodatkowe Wskazówki i Porady
- Zapisuj wszystkie kroki obliczeń. To pomoże Ci uniknąć błędów i łatwiej zlokalizować ewentualne pomyłki.
- Używaj kalkulatora, aby sprawdzić swoje wyniki. To da Ci pewność, że obliczenia są poprawne.
- Jeśli masz problem, nie wstydź się pytać! Nauczyciel, kolega lub rodzic na pewno chętnie Ci pomogą.
- Pamiętaj, że nauka matematyki to proces. Nie zrażaj się, jeśli na początku coś Ci nie wychodzi. Z czasem wszystko stanie się prostsze.
Motywacja i Zachęta
Matematyka nie musi być nudna i trudna! Traktuj ją jak wyzwanie, które możesz pokonać. Każde rozwiązane zadanie to mały sukces, który przybliża Cię do celu. Pamiętaj, że inwestycja w naukę to najlepsza inwestycja w przyszłość! Zatem, do dzieła! Obliczaj, eksperymentuj i ciesz się z osiągniętych rezultatów. Wierzę w Ciebie!
Na koniec, pamiętaj, że kluczem do sukcesu jest cierpliwość i systematyczność. Nie zniechęcaj się drobnymi niepowodzeniami, a z każdym kolejnym zadaniem poczujesz się pewniej i bardziej kompetentnie. Trzymam kciuki!