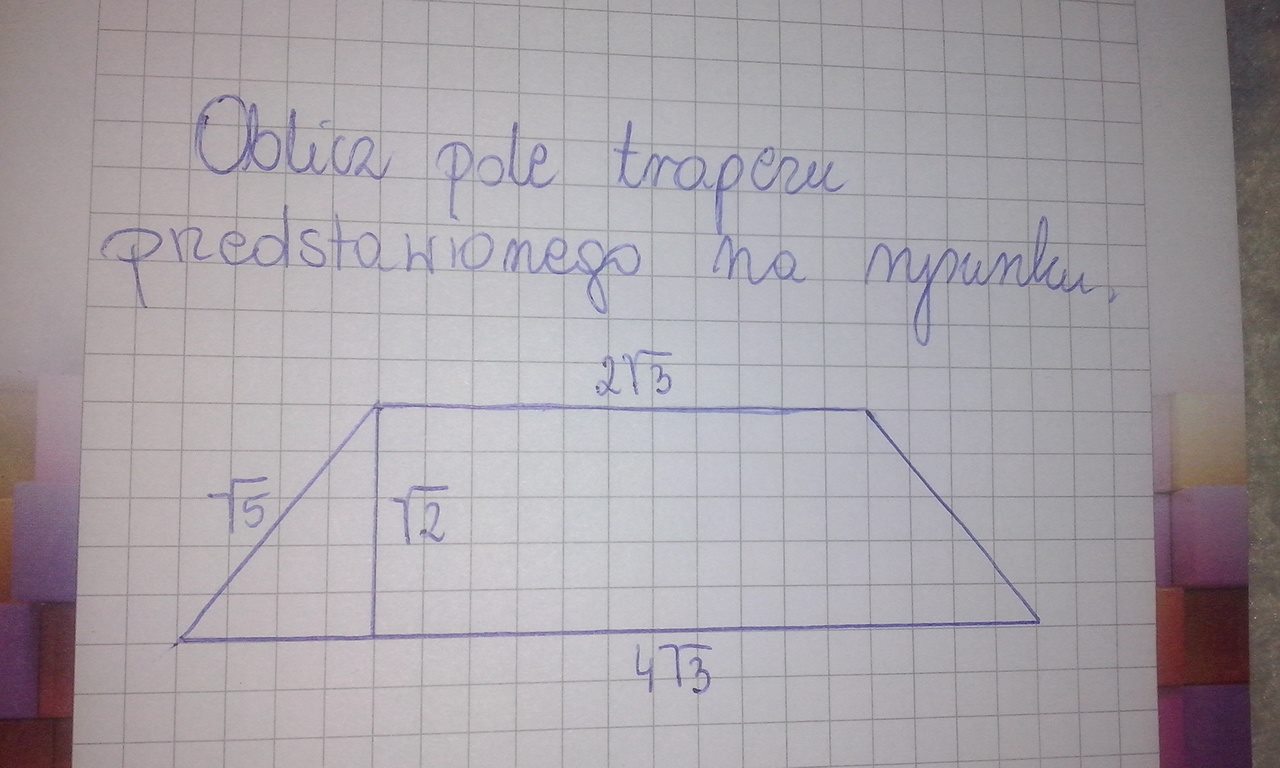
Oblicz Pole Trapezu Przedstawionego Na Rysunku

Witaj! Zmagasz się z obliczaniem pola trapezu przedstawionego na rysunku? Nie martw się, nie jesteś sam! Wielu uczniów i studentów ma problem z geometrią, a obliczanie pól figur bywa wyjątkowo kłopotliwe. Często spotykam się z pytaniami: "Jak to zrobić?", "Czy jest na to jakiś prosty sposób?" Postaram się w tym artykule rozwiać wszelkie Twoje wątpliwości i krok po kroku wyjaśnić, jak obliczyć pole trapezu. Zrozumienie tego zagadnienia otwiera drzwi do rozwiązywania bardziej złożonych problemów geometrycznych i przydaje się w wielu praktycznych sytuacjach.

Dlaczego Obliczanie Pola Trapezu Jest Ważne?

Możesz pomyśleć, że obliczanie pola trapezu to czysta teoria, która nigdy Ci się nie przyda w życiu. Nic bardziej mylnego! Umiejętność ta ma wiele zastosowań w realnym świecie. Pomyśl o:

Architekturze i budownictwie: Projektowanie dachów, obliczanie ilości materiałów potrzebnych do wykończenia elewacji, gdzie często mamy do czynienia z trapezami.
Ogrodnictwie i krajobrazie: Wyznaczanie powierzchni rabat, klombów czy ścieżek, które mają kształt trapezu.
Projektowaniu wnętrz: Obliczanie powierzchni ścian, które mają nieregularny kształt i można je przybliżyć trapezami.
Geodezji: Pomiar powierzchni działek o nieregularnych kształtach.

Widzisz więc, że to nie tylko zadanie z podręcznika, ale praktyczna umiejętność, która może Ci się przydać w wielu sytuacjach zawodowych i codziennych.

Czym Właściwie Jest Trapez?

Zanim przejdziemy do wzoru na pole trapezu, upewnijmy się, że dobrze rozumiemy, czym on jest. Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu (zwykle oznaczane jako a i b). Pozostałe dwa boki to ramiona trapezu.

Ważne jest rozróżnienie różnych rodzajów trapezów:

Trapez równoramienny: Ma ramiona równej długości. Kąty przy każdej z podstaw są równe.
Trapez prostokątny: Ma co najmniej jeden kąt prosty.
Trapez różnoboczny: Ma wszystkie boki różnej długości.

Wzór na pole trapezu jest uniwersalny i działa dla każdego rodzaju trapezu. Nie musisz się martwić, jaki to dokładnie rodzaj, aby obliczyć jego pole.

Wzór na Pole Trapezu – Klucz do Sukcesu

Wzór na pole trapezu jest prosty i łatwy do zapamiętania. Brzmi on następująco:

P = (a + b) * h / 2

Gdzie:

P – pole trapezu
a – długość jednej podstawy
b – długość drugiej podstawy
h – wysokość trapezu (odległość między podstawami)

Zwróć uwagę, że wysokość trapezu jest zawsze mierzona prostopadle do podstaw. Czasami na rysunku wysokość może być narysowana jako linia poza trapezem, ale nadal mierzy ona odległość między podstawami.

Krok po Kroku: Jak Obliczyć Pole Trapezu na Rysunku?

Załóżmy, że masz rysunek trapezu i musisz obliczyć jego pole. Oto kroki, które powinieneś wykonać:

Zidentyfikuj podstawy (a i b): Znajdź dwa boki równoległe trapezu. Zmierz ich długości.
Zidentyfikuj wysokość (h): Znajdź linię prostopadłą do podstaw. Zmierz jej długość. Jeśli wysokość nie jest narysowana, spróbuj ją wywnioskować z innych danych na rysunku (np. używając twierdzenia Pitagorasa, jeśli masz trójkąt prostokątny).
Podstaw wartości do wzoru: Wstaw wartości a, b i h do wzoru P = (a + b) * h / 2.
Wykonaj obliczenia: Najpierw dodaj długości podstaw (a + b), następnie pomnóż wynik przez wysokość (h), a na koniec podziel przez 2.
Podaj wynik z jednostką: Pamiętaj o podaniu wyniku z odpowiednią jednostką. Jeśli długości boków były podane w centymetrach (cm), to pole będzie wyrażone w centymetrach kwadratowych (cm²).

Przykład Praktyczny

Wyobraź sobie, że masz trapez, którego podstawy mają długości 5 cm i 7 cm, a wysokość wynosi 4 cm. Obliczmy jego pole:

a = 5 cm
b = 7 cm
h = 4 cm

Podstawiamy do wzoru:

P = (5 cm + 7 cm) * 4 cm / 2

P = 12 cm * 4 cm / 2

P = 48 cm² / 2

P = 24 cm²

Zatem pole tego trapezu wynosi 24 cm².

Częste Błędy i Jak Ich Unikać

Podczas obliczania pola trapezu można popełnić kilka typowych błędów. Oto one i sposoby ich uniknięcia:

Pomylenie podstaw z ramionami: Pamiętaj, że podstawy to boki równoległe.
Użycie nieprawidłowej wysokości: Wysokość musi być prostopadła do podstaw. Często na rysunku podawana jest długość ramienia, która nie jest wysokością.
Błędy w obliczeniach: Sprawdź dokładnie swoje obliczenia, zwłaszcza mnożenie i dzielenie.
Zapomnienie o jednostce: Pamiętaj o podaniu wyniku z odpowiednią jednostką kwadratową.

Adresowanie Kontrargumentów: Co, jeśli Brakuje Danych?

Czasami na rysunku brakuje informacji o długościach podstaw lub wysokości. W takiej sytuacji musisz poszukać innych danych, które pozwolą Ci je wyliczyć. Możesz skorzystać z:

Twierdzenia Pitagorasa: Jeśli masz trójkąt prostokątny w trapezie, możesz obliczyć długość boku, znając długości pozostałych dwóch boków.
Własności trapezów równoramiennych: W trapezach równoramiennych kąty przy podstawach są równe, co może pomóc w wyliczeniu brakujących długości.
Trygonometrii: Jeśli znasz kąty i długość jednego boku, możesz obliczyć długości pozostałych boków.

Czasami trzeba podzielić trapez na mniejsze figury (np. prostokąt i trójkąty), obliczyć ich pola, a następnie je zsumować, aby otrzymać pole całego trapezu.

Alternatywne Metody Obliczania Pola

Oprócz standardowego wzoru P = (a + b) * h / 2 istnieją alternatywne metody obliczania pola trapezu, które mogą być przydatne w specyficznych sytuacjach:

Użycie linii środkowej: Linia środkowa trapezu łączy środki ramion. Jej długość jest równa średniej arytmetycznej długości podstaw, czyli (a + b) / 2. Pole trapezu można wtedy obliczyć jako P = m * h, gdzie m to długość linii środkowej.
Podział na trójkąty: Można podzielić trapez na dwa trójkąty, prowadząc przekątną. Następnie obliczyć pola tych trójkątów i je zsumować.

Podsumowanie i Co Dalej?

Obliczanie pola trapezu na rysunku, choć na początku może wydawać się trudne, staje się proste, gdy zrozumiesz podstawowe pojęcia i wzór. Pamiętaj o zidentyfikowaniu podstaw, wysokości, podstawieniu wartości do wzoru i wykonaniu obliczeń. Unikaj częstych błędów i korzystaj z alternatywnych metod, gdy brakuje danych.

Teraz, gdy już wiesz, jak obliczyć pole trapezu, zachęcam Cię do:

Przećwiczenia na różnych przykładach: Znajdź rysunki trapezów w podręcznikach, internecie lub stwórz własne i spróbuj obliczyć ich pola.
Rozwiązywania zadań tekstowych: Zadania tekstowe pozwolą Ci zrozumieć, jak wykorzystać wiedzę o polu trapezu w praktycznych sytuacjach.
Dzielenia się wiedzą z innymi: Wyjaśnij komuś, jak obliczyć pole trapezu. Uczenie innych utrwala wiedzę!

Czy masz teraz większą pewność siebie w obliczaniu pola trapezu? Jakie zagadnienia geometryczne sprawiają Ci trudności? Może to będzie temat mojego następnego artykułu! Powodzenia!