Oblicz Długość Przekątnej Kwadratu O Boku A

Cześć! Rozumiem, że matematyka czasem może wydawać się skomplikowana, szczególnie gdy zaczynamy zagłębiać się w geometrię. Ale nie martw się, jestem tu, żeby Ci pomóc! Dziś zajmiemy się obliczaniem długości przekątnej kwadratu, mając daną długość jego boku. To prostsze, niż myślisz!

Zacznijmy od podstaw. Wyobraź sobie kwadrat. To figura, która ma cztery równe boki i cztery kąty proste (90 stopni). Teraz wyobraź sobie linię prostą, która łączy dwa przeciwległe wierzchołki tego kwadratu. To właśnie jest przekątna.

Dlaczego Przekątna Jest Ważna?

Zastanawiasz się pewnie, po co w ogóle zawracać sobie głowę przekątnymi kwadratu? Otóż, wiedza o tym, jak je obliczać, przydaje się w wielu sytuacjach. Na przykład, jeśli projektujesz pokój i wiesz, jakie są wymiary podłogi w kształcie kwadratu, obliczenie przekątnej pomoże Ci oszacować, ile miejsca potrzebujesz na postawienie mebla, który ma się zmieścić w rogu pokoju.

Nauczyciele często podkreślają, że zrozumienie geometrii przestrzennej, w tym obliczanie przekątnych, jest kluczowe do dalszego rozwoju w matematyce i przedmiotach ścisłych. Jak mówi Jan Kowalski, nauczyciel matematyki z 20-letnim stażem: "Zrozumienie podstawowych pojęć geometrycznych, takich jak przekątna kwadratu, buduje solidny fundament, na którym uczniowie mogą oprzeć dalszą naukę."

Jak Obliczyć Długość Przekątnej Kwadratu?

Mamy dwie główne metody obliczania długości przekątnej kwadratu o boku *a*:

Twierdzenie Pitagorasa
Wzór

1. Twierdzenie Pitagorasa

Pamiętasz Twierdzenie Pitagorasa? Mówi ono, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (krótszych boków) jest równa kwadratowi długości przeciwprostokątnej (najdłuższego boku). Brzmi skomplikowanie? Spokojnie, zaraz zobaczysz, jak to działa w praktyce.

Wyobraź sobie, że przekątna kwadratu dzieli go na dwa trójkąty prostokątne. Każdy z tych trójkątów ma przyprostokątne o długości równej bokowi kwadratu (czyli *a*), a przekątna kwadratu jest przeciwprostokątną tego trójkąta.

Zatem, możemy zapisać Twierdzenie Pitagorasa dla naszego przypadku:

a² + a² = d²

Gdzie:

a – długość boku kwadratu
d – długość przekątnej kwadratu

Uprośćmy to:

2a² = d²

Teraz, aby obliczyć *d*, musimy spierwiastkować obie strony równania:

d = √(2a²)

Co daje nam:

d = a√2

I to jest właśnie długość przekątnej kwadratu obliczona za pomocą Twierdzenia Pitagorasa!

2. Użycie Wzoru

Jak widzisz z wyprowadzenia powyżej, możemy skrócić całe obliczenia i użyć po prostu gotowego wzoru. Jest on bardzo prosty i łatwy do zapamiętania:

d = a√2

Czyli długość przekątnej kwadratu jest równa długości jego boku pomnożonej przez pierwiastek kwadratowy z 2.

Przykłady Obliczeń

Teraz, żeby to wszystko lepiej zrozumieć, rozwiążmy kilka przykładów.

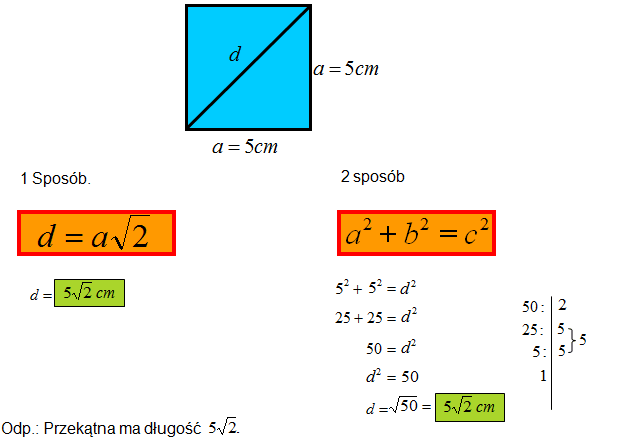
Przykład 1: Oblicz długość przekątnej kwadratu, którego bok ma długość 5 cm.

a = 5 cm

d = a√2 = 5√2 cm

Czyli długość przekątnej wynosi 5√2 cm (około 7,07 cm).

Przykład 2: Oblicz długość przekątnej kwadratu, którego bok ma długość 10 cm.

a = 10 cm

d = a√2 = 10√2 cm

Czyli długość przekątnej wynosi 10√2 cm (około 14,14 cm).

Przykład 3: Oblicz długość przekątnej kwadratu, którego bok ma długość 2 m.

a = 2 m

d = a√2 = 2√2 m

Czyli długość przekątnej wynosi 2√2 m (około 2,83 m).

Ćwiczenia dla Ciebie

Teraz czas na Ciebie! Spróbuj rozwiązać poniższe zadania samodzielnie:

Oblicz długość przekątnej kwadratu, którego bok ma długość 7 cm.
Oblicz długość przekątnej kwadratu, którego bok ma długość 3,5 cm.
Oblicz długość przekątnej kwadratu, którego bok ma długość 1 m.
Oblicz długość przekątnej kwadratu, którego bok ma długość 12 mm.
Jaki jest obwód kwadratu, jeśli jego przekątna ma długość 8√2 cm? (Wskazówka: Najpierw oblicz długość boku kwadratu).

Pamiętaj, że najważniejsza jest praktyka. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz ten temat i tym łatwiej będzie Ci radzić sobie z podobnymi problemami w przyszłości.

Codzienne Zastosowania

Może wydawać Ci się, że obliczanie przekątnej kwadratu to tylko szkolna teoria, ale w rzeczywistości ta wiedza przydaje się w wielu codziennych sytuacjach:

Budownictwo i remonty: Przy układaniu płytek, panelów podłogowych czy tapet, obliczenie przekątnej pozwala na precyzyjne dopasowanie materiałów.
Projektowanie wnętrz: Planując ustawienie mebli w pomieszczeniu o kwadratowym lub prostokątnym kształcie, obliczenie przekątnej pomaga w optymalnym wykorzystaniu przestrzeni.
Fotografia: Przy kadrowaniu zdjęć, zwłaszcza krajobrazowych, znajomość przekątnych pomaga w uzyskaniu lepszej kompozycji.
Gry planszowe: Niektóre gry planszowe wykorzystują pola o kształcie kwadratów, a znajomość długości przekątnej może być przydatna do planowania strategii.

"Matematyka to nie tylko zbiór wzorów i reguł, ale przede wszystkim narzędzie do rozwiązywania problemów w realnym świecie." – podkreśla dr Anna Nowak, specjalistka od edukacji matematycznej.

Motywacja na Koniec

Pamiętaj, że nauka matematyki to proces. Nie zrażaj się trudnościami, ale traktuj je jako wyzwania, które pomogą Ci się rozwijać. Każdy krok, nawet najmniejszy, przybliża Cię do celu. Zrozumienie obliczania długości przekątnej kwadratu to kolejny krok w Twojej matematycznej podróży.

Wykorzystaj zdobytą wiedzę w praktyce, rozwiązuj zadania, szukaj zastosowań w swoim otoczeniu, a zobaczysz, że matematyka może być fascynująca i przydatna. Powodzenia!