Na Rysunku Obok Przedstawiono Wykres Funkcji F
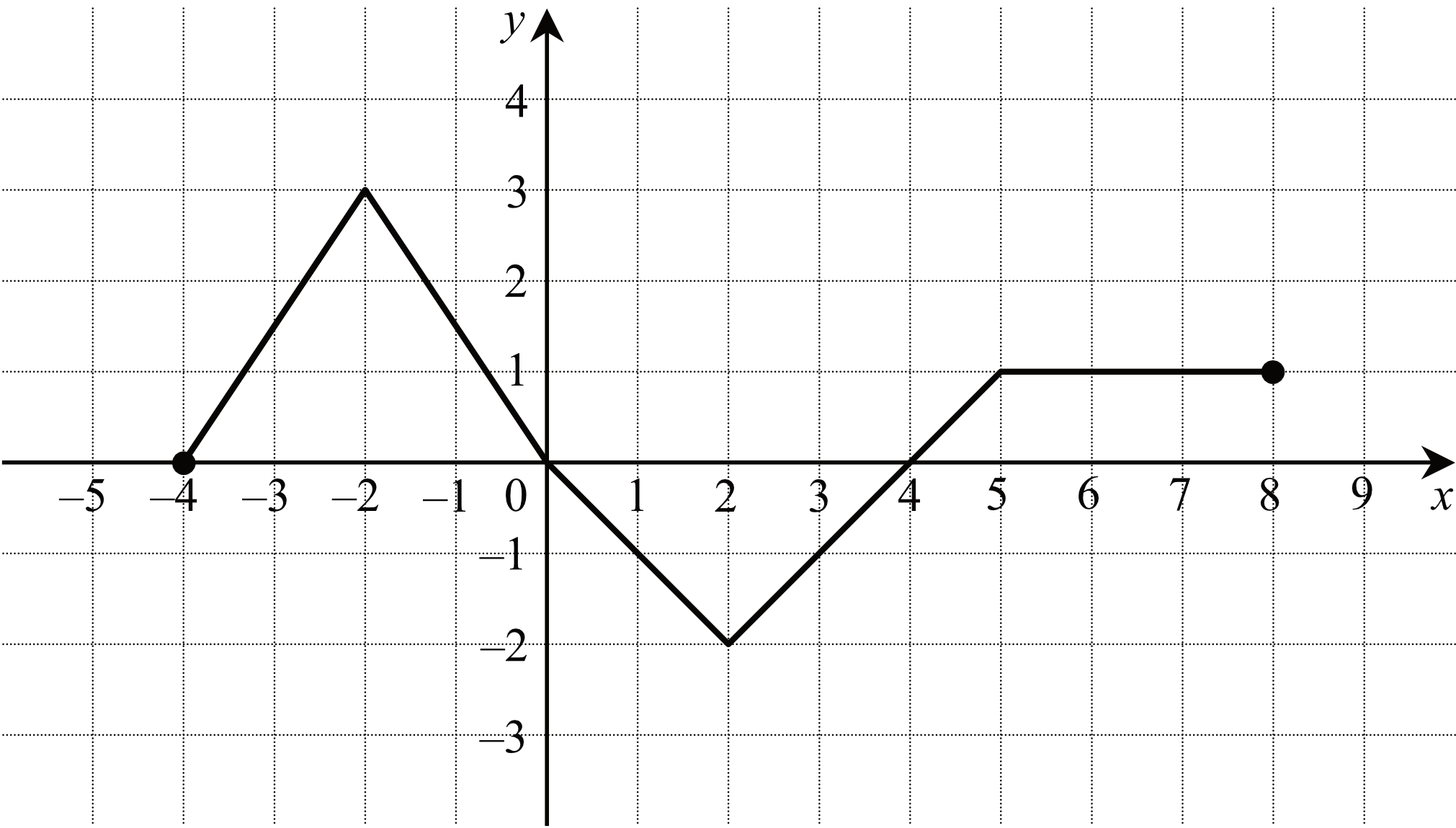
"Na Rysunku Obok Przedstawiono Wykres Funkcji F" to fraza, która pojawia się często w zadaniach matematycznych i oznacza dosłownie: "Na rysunku obok przedstawiono wykres funkcji F". Kluczowe jest tutaj zrozumienie, że wykres funkcji F to wizualna reprezentacja związku między argumentami (zwykle oznaczanymi jako x) a wartościami funkcji (zwykle oznaczanymi jako y lub f(x)). Innymi słowy, każdy punkt na tym wykresie ma współrzędne (x, f(x)) i pokazuje, jaką wartość funkcja F przyjmuje dla danego x.
Krok 1: Odczytywanie wartości funkcji z wykresu. Załóżmy, że wykres funkcji F jest narysowany. Aby odczytać wartość f(a) (wartość funkcji dla x=a), znajdź punkt na osi x, gdzie x=a. Następnie przesuń się pionowo (w górę lub w dół) aż do przecięcia z wykresem funkcji. Współrzędna y punktu przecięcia to wartość f(a).
Przykład: Jeśli na wykresie funkcji widzimy punkt (2, 3), oznacza to, że f(2) = 3. Czyli, kiedy x wynosi 2, funkcja F przyjmuje wartość 3.
Krok 2: Znajdowanie argumentów dla danej wartości funkcji. Chcemy znaleźć x, dla którego f(x) = b. Znajdź punkt na osi y, gdzie y=b. Następnie przesuń się poziomo (w lewo lub w prawo) aż do przecięcia z wykresem funkcji. Współrzędna x punktu przecięcia to szukany argument.
Przykład: Jeśli chcemy znaleźć x takie, że f(x) = 5, szukamy punktu na wykresie, którego współrzędna y wynosi 5. Jeśli widzimy punkt (4, 5) na wykresie, to oznacza, że f(4) = 5, czyli x=4 jest rozwiązaniem.
Krok 3: Określanie dziedziny i zbioru wartości. Dziedzina funkcji to zbiór wszystkich dopuszczalnych wartości x, dla których funkcja jest zdefiniowana. Patrząc na wykres, spójrz na najmniejszą i największą wartość x, dla której wykres istnieje. Zbiór wartości to zbiór wszystkich wartości y, jakie funkcja przyjmuje. Analogicznie, patrzymy na najniższą i najwyższą wartość y, którą osiąga wykres.
Przykład: Jeśli wykres funkcji rozciąga się od x=-3 do x=5, to dziedzina to przedział [-3, 5]. Jeśli wartości y mieszczą się w przedziale od y=1 do y=7, to zbiór wartości to przedział [1, 7].
Krok 4: Analiza zachowania funkcji. Z wykresu można odczytać, czy funkcja jest rosnąca, malejąca, stała, gdzie ma ekstrema (maksima i minima), punkty przecięcia z osiami, oraz czy jest ciągła.
Przykład: Jeśli wykres funkcji idzie w górę (y rośnie) w miarę jak przesuwamy się w prawo (x rośnie), to funkcja jest rosnąca w tym przedziale. Jeśli wykres idzie w dół, to funkcja jest malejąca.
Dlaczego to jest ważne? Analiza wykresów funkcji jest kluczowa w wielu dziedzinach. W ekonomii pozwala na wizualizację trendów rynkowych. Na przykład, wykres popytu i podaży pomaga zrozumieć zmiany cen. W fizyce wykresy przedstawiają zależność prędkości od czasu, co pozwala analizować ruch ciał. Umiejętność interpretacji "Na Rysunku Obok Przedstawiono Wykres Funkcji F" daje więc mocną podstawę do zrozumienia i analizy danych w wielu różnych obszarach.








