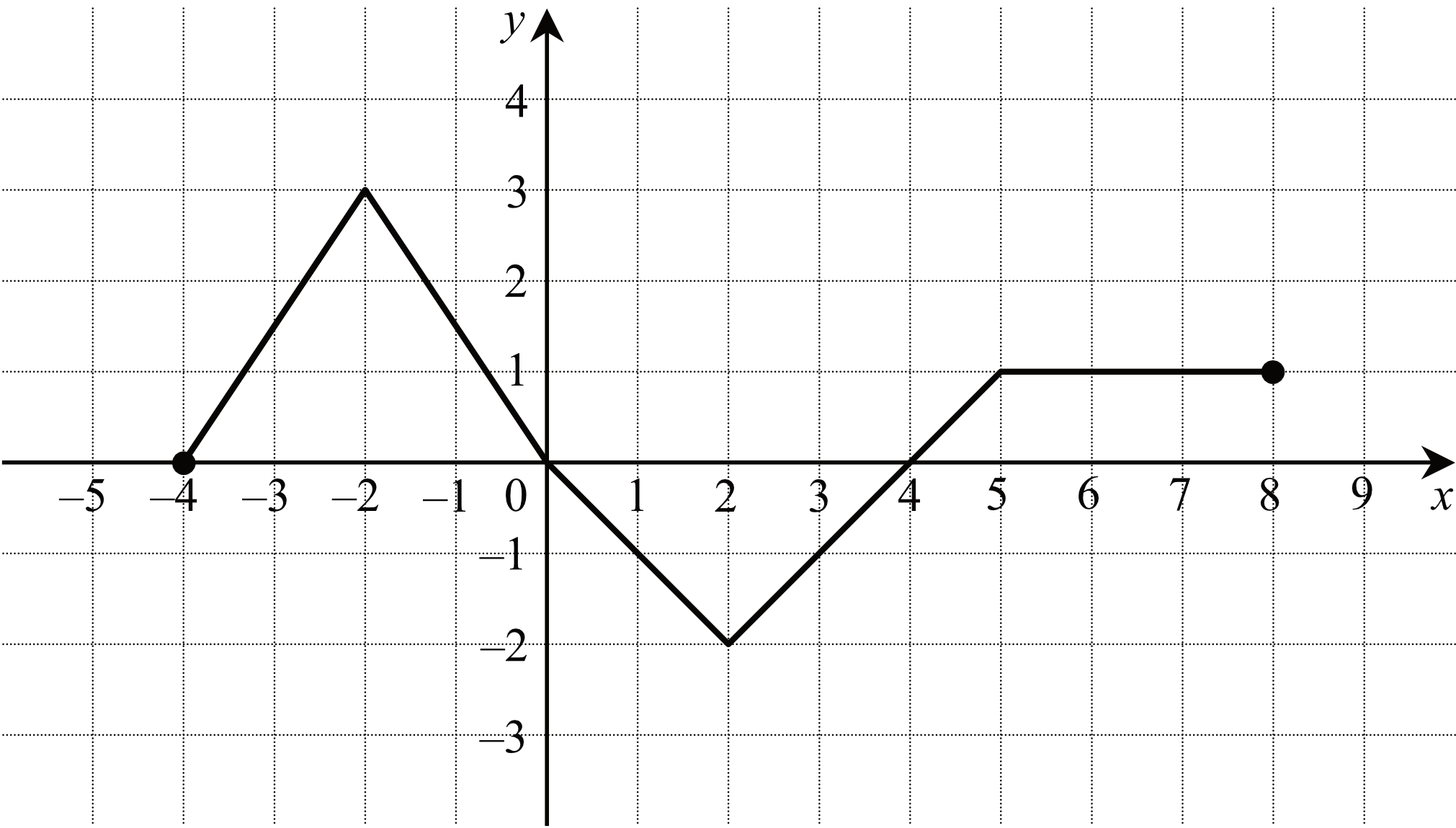
Na Rysunku Obok Dany Jest Wykres Funkcji F

Analiza wykresu funkcji, czyli "Na rysunku obok dany jest wykres funkcji f", to fundament matematyki. Umiejętność interpretacji wykresów jest niezbędna w wielu dziedzinach. Ważne, by uczniowie opanowali tę umiejętność.

Jak rozpocząć? Zacznij od podstaw. Skup się na osiach x i y. Wyjaśnij, co reprezentują. Określ punkty przecięcia wykresu z osiami. To punkty, które łatwo zidentyfikować i opisać.

Kolejny krok to dziedzina i zbiór wartości. Dziedzina to wszystkie możliwe wartości x, dla których funkcja jest zdefiniowana. Zbiór wartości to wszystkie możliwe wartości y, które funkcja przyjmuje. Pokaż, jak odczytać te informacje z wykresu.

Miejsca zerowe to punkty, w których wykres przecina oś x. W tych punktach wartość funkcji (y) jest równa zero. Wyraźnie zaznacz to powiązanie. Użyj kolorów, by to uwidocznić.

Monotoniczność funkcji to kolejny ważny aspekt. Określ przedziały, w których funkcja rośnie, maleje lub jest stała. Użyj strzałek na wykresie, by to zilustrować. Pamiętaj, aby mówić o przedziałach na osi x.

Ekstrema lokalne (maksima i minima) to punkty, w których funkcja osiąga swoje lokalne wartości największe i najmniejsze. Wyjaśnij, jak je znaleźć na wykresie. Podkreśl, że są to wartości lokalne, a niekoniecznie globalne.

Sposoby na zaangażowanie uczniów? Użyj interaktywnych narzędzi. Programy do rysowania wykresów, jak GeoGebra, są bardzo pomocne. Pozwalają eksperymentować i obserwować zmiany na wykresie w czasie rzeczywistym.

Ćwiczenia praktyczne są kluczowe. Daj uczniom różne wykresy do analizy. Poproś ich o opisanie ich cech. Zachęć do pracy w grupach. Wymiana wiedzy między uczniami to cenny element procesu uczenia się.

Typowe błędy uczniów? Często mylą dziedzinę ze zbiorem wartości. Myślą, że miejsca zerowe to punkty na osi y. Ważne, by te błędy regularnie korygować. Powtarzanie i utrwalanie wiedzy jest niezbędne.

Uczniowie często mają problem z zapisywaniem przedziałów monotoniczności. Pamiętaj, by zawsze odnosić się do osi x. Ćwicz zapisywanie przedziałów na tablicy. Daj uczniom przykłady do samodzielnego rozwiązania.

Podsumowując, analiza wykresu funkcji to ważna umiejętność. Kluczem do sukcesu jest systematyczna praca i powtarzanie. Używaj interaktywnych narzędzi i ćwiczeń praktycznych. Pamiętaj o korygowaniu typowych błędów. Dzięki temu uczniowie zdobędą solidne podstawy matematyczne.

Wykorzystuj kontekst. Połącz analizę wykresów z sytuacjami z życia codziennego. Na przykład, wykres temperatury w ciągu dnia. Albo wykres zależności odległości od czasu podczas podróży. To ułatwi uczniom zrozumienie sensu analizy wykresów. Uczniowie zobaczą wtedy praktyczne zastosowanie matematyki.