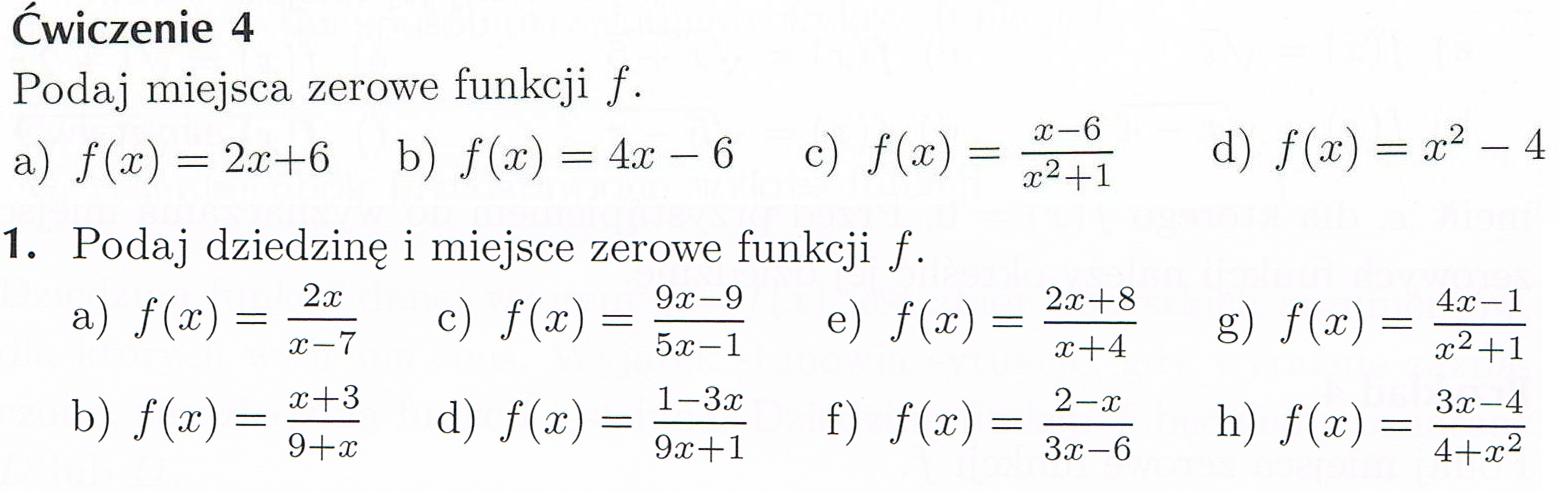Miejsca Zerowe Funkcji Gimnazjum Sprawdzian Drukuj

Cześć! Jestem tu, żeby pomóc Wam przygotować się do sprawdzianu z miejsc zerowych funkcji. Nie martwcie się, to temat, który da się zrozumieć i opanować. Razem przejdziemy przez najważniejsze rzeczy.
Miejsca zerowe funkcji, inaczej zwane pierwiastkami funkcji, to takie wartości argumentu (czyli liczby, którą wstawiamy do funkcji, najczęściej oznaczone jako 'x'), dla których wartość funkcji (czyli wynik działania funkcji, często oznaczony jako 'f(x)' lub 'y') jest równa zero. Mówiąc prościej, szukamy takich 'x', dla których f(x) = 0.
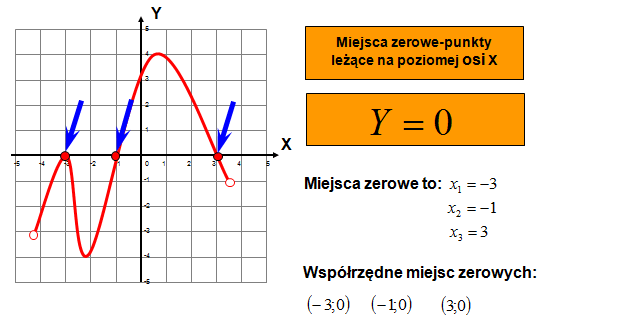
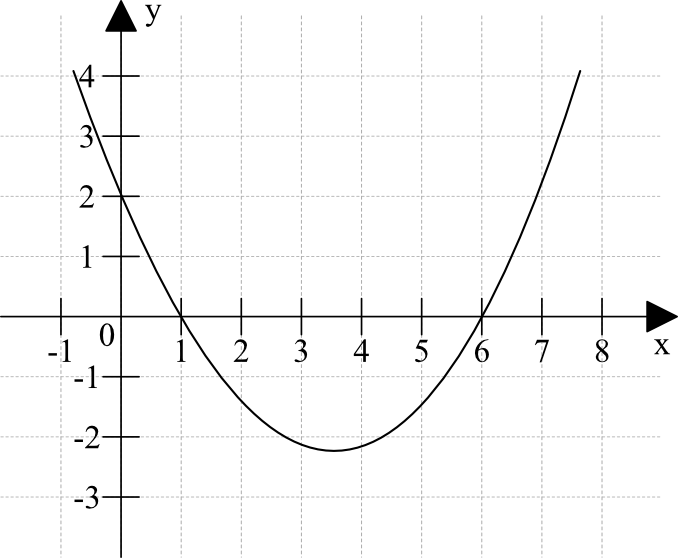
Wyobraźcie sobie wykres funkcji. Miejsca zerowe to punkty, w których ten wykres przecina oś X. Kiedy wykres dotyka osi X lub ją przecina, wysokość (czyli wartość 'y' lub 'f(x)') wynosi dokładnie zero. Dlatego właśnie szukamy tych punktów.
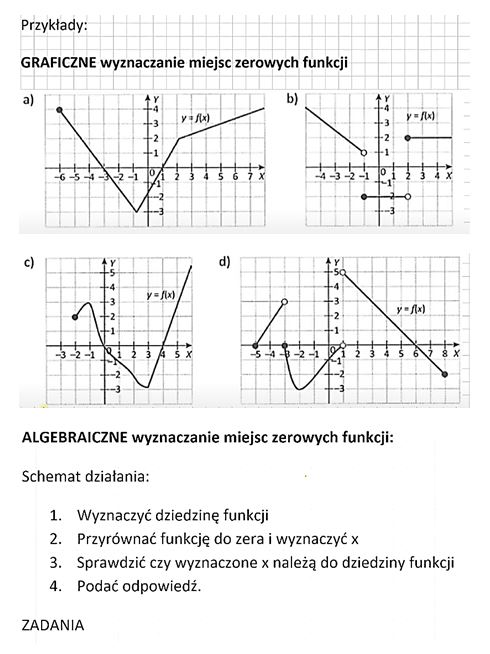
Jak znaleźć miejsca zerowe? Najczęściej rozwiązujemy równanie f(x) = 0. Sposób rozwiązania tego równania zależy od typu funkcji, którą mamy.
Dla funkcji liniowej, która ma postać f(x) = ax + b (gdzie 'a' i 'b' to liczby, a 'a' nie jest zerem), rozwiązanie jest proste. Wystarczy przyrównać funkcję do zera i rozwiązać równanie:
ax + b = 0
Przenosimy 'b' na drugą stronę:
ax = -b
A następnie dzielimy przez 'a':
x = -b/a
To właśnie jest nasze miejsce zerowe dla funkcji liniowej. Zawsze będzie jedno, o ile 'a' nie jest zerem.
Dla funkcji kwadratowej, czyli takiej, która ma postać f(x) = ax² + bx + c (gdzie 'a' nie jest zerem), sprawa jest nieco bardziej złożona. Tutaj musimy skorzystać z wzoru na pierwiastki równania kwadratowego. Najpierw obliczamy wyróżnik funkcji, czyli deltę (Δ).
Δ = b² - 4ac
Od wartości delty zależą miejsca zerowe:
- Jeśli Δ > 0, funkcja ma dwa różne miejsca zerowe. Obliczamy je ze wzorów: x₁ = (-b - √Δ) / 2a oraz x₂ = (-b + √Δ) / 2a.
- Jeśli Δ = 0, funkcja ma jedno miejsce zerowe (nazywane też podwójnym). Obliczamy je ze wzoru: x₀ = -b / 2a.
- Jeśli Δ < 0, funkcja nie ma miejsc zerowych w zbiorze liczb rzeczywistych.
Pamiętajcie, że kluczem do sukcesu jest uważne czytanie poleceń i zastosowanie właściwego wzoru. Ćwiczenie czyni mistrza, więc rozwiążcie jak najwięcej przykładów.
Podsumowując:
Miejsca zerowe to wartości 'x', dla których f(x) = 0. Na wykresie to punkty przecięcia z osią X.
Dla funkcji liniowej f(x) = ax + b, miejsce zerowe to x = -b/a.
Dla funkcji kwadratowej f(x) = ax² + bx + c, szukamy pierwiastków równania ax² + bx + c = 0, korzystając z delty (Δ) i jej wartości.
Powodzenia na sprawdzianie! Jesteście w stanie to zrobić!