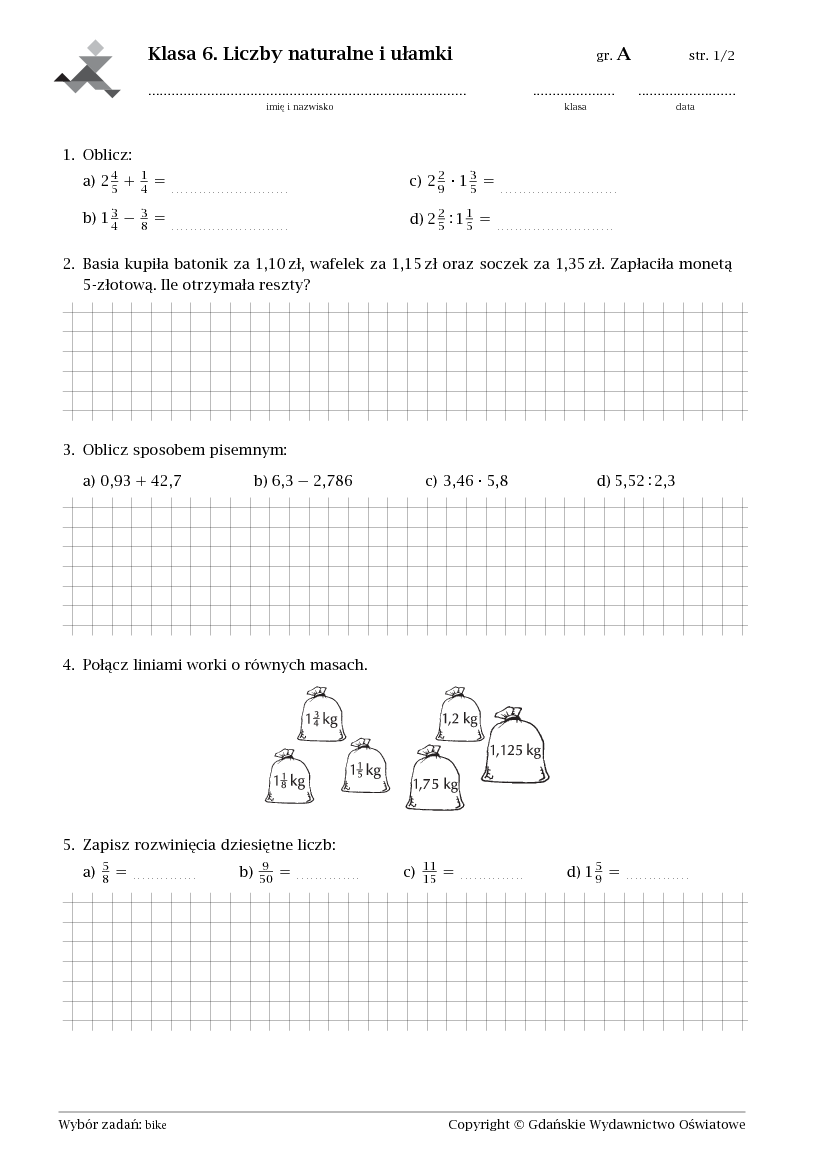
Matematyka Z Plusem Klasa 6 Sprawdzian Liczby Naturalne I Ułamki

Czy zbliża się sprawdzian z matematyki, a Ty czujesz, że liczby naturalne i ułamki to wciąż czarna magia? Spokojnie, nie jesteś sam! Wielu uczniów klasy 6 ma podobne odczucia. Ten artykuł jest właśnie dla Ciebie – ucznia klasy 6 przygotowującego się do sprawdzianu z działu "Liczby Naturalne i Ułamki" w oparciu o podręcznik "Matematyka z Plusem". Razem przejdziemy przez najważniejsze zagadnienia, przypomnimy kluczowe definicje i pokażemy, jak radzić sobie z typowymi zadaniami. Naszym celem jest, abyś podszedł do sprawdzianu pewny swojej wiedzy i umiejętności.

Podstawy Liczb Naturalnych: Powtórka Przed Sprawdzianem

Liczby naturalne to liczby, których używamy do liczenia przedmiotów. Pamiętasz, jak zaczynałeś liczyć na palcach? 1, 2, 3... To właśnie liczby naturalne! Są one całkowite i dodatnie. Zero również zalicza się do zbioru liczb naturalnych (choć w niektórych definicjach nie jest uwzględniane, ale w "Matematyce z Plusem" zazwyczaj tak!).

Działania na Liczbach Naturalnych

Podstawowe działania to:

Dodawanie: Łączenie dwóch lub więcej liczb. Pamiętaj o kolejności wykonywania działań, jeśli masz kilka operacji w jednym przykładzie!
Odejmowanie: Określanie różnicy między dwiema liczbami. Upewnij się, że odejmujesz od większej liczby (w zbiorze liczb naturalnych).
Mnożenie: Skrócony zapis dodawania tej samej liczby wiele razy. Pamiętaj o tabliczce mnożenia!
Dzielenie: Rozdzielanie liczby na równe części. Sprawdź, czy wynik jest liczbą naturalną (dzielenie z resztą omówimy później).

Pamiętaj o kolejności wykonywania działań! Najpierw nawiasy, potem mnożenie i dzielenie (od lewej do prawej), a na końcu dodawanie i odejmowanie (również od lewej do prawej). "Matematyka z Plusem" na pewno poświęca temu sporo uwagi.

Przykład: 2 + 3 * 4 = 2 + 12 = 14 (a nie 5 * 4 = 20!)

Dzielenie z Resztą

Często nie da się podzielić jednej liczby naturalnej przez drugą tak, aby otrzymać w wyniku liczbę naturalną. Wtedy mamy dzielenie z resztą. Reszta zawsze musi być mniejsza od dzielnika.

Przykład: 17 : 5 = 3 reszty 2 (bo 3 * 5 = 15, a 17 - 15 = 2)

Upewnij się, że rozumiesz, jak to działa! To często pojawia się na sprawdzianach.

Ułamki: Pokonujemy Strach Przed Licznikami i Mianownikami

Ułamek to sposób zapisu części całości. Składa się z:

Licznika: Liczba znajdująca się nad kreską ułamkową. Pokazuje, ile części całości bierzemy.
Mianownika: Liczba znajdująca się pod kreską ułamkową. Pokazuje, na ile równych części podzielona jest całość.

Pamiętaj! Mianownik nigdy nie może być równy zero!

Rodzaje Ułamków

Ułamek właściwy: Licznik jest mniejszy od mianownika (np. 1/2, 3/4). Ułamek właściwy jest zawsze mniejszy od 1.
Ułamek niewłaściwy: Licznik jest większy lub równy mianownikowi (np. 5/3, 7/7). Ułamek niewłaściwy jest większy lub równy 1.
Liczba mieszana: Składa się z liczby całkowitej i ułamka właściwego (np. 1 2/3, 2 1/4). To po prostu inny sposób zapisu ułamka niewłaściwego.

Zamiana Ułamków Niewłaściwych na Liczby Mieszane i Odwrotnie

To bardzo ważna umiejętność! Na sprawdzianie na pewno się przyda.

Ułamek niewłaściwy na liczbę mieszaną: Dzielimy licznik przez mianownik. Wynik dzielenia to liczba całkowita liczby mieszanej, reszta to licznik ułamka, a mianownik pozostaje ten sam.

Przykład: 11/4 = 2 reszty 3, więc 11/4 = 2 3/4

Liczba mieszana na ułamek niewłaściwy: Mnożymy liczbę całkowitą przez mianownik, dodajemy licznik, a mianownik pozostaje ten sam.

Przykład: 3 1/2 = (3 * 2 + 1) / 2 = 7/2

Rozszerzanie i Skracanie Ułamków

Rozszerzanie ułamka: Mnożymy licznik i mianownik przez tę samą liczbę (różną od zera). Wartość ułamka się nie zmienia, tylko zmienia się jego zapis.

Przykład: 1/2 = (1 * 2) / (2 * 2) = 2/4 = (1 * 5) / (2 * 5) = 5/10

Skracanie ułamka: Dzielimy licznik i mianownik przez tę samą liczbę (różną od zera). Wartość ułamka się nie zmienia, tylko zapis staje się prostszy.

Przykład: 6/8 = (6 : 2) / (8 : 2) = 3/4

Szukaj największego wspólnego dzielnika (NWD) licznika i mianownika, aby skrócić ułamek do postaci nieskracalnej.

Działania na Ułamkach

Dodawanie i odejmowanie ułamków o jednakowych mianownikach: Dodajemy (lub odejmujemy) liczniki, a mianownik pozostaje ten sam.
Dodawanie i odejmowanie ułamków o różnych mianownikach: Najpierw sprowadzamy ułamki do wspólnego mianownika (najczęściej najmniejszej wspólnej wielokrotności – NWW mianowników), a następnie dodajemy (lub odejmujemy) liczniki.
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik.
Dzielenie ułamków: Mnożymy pierwszy ułamek przez odwrotność drugiego ułamka (zamieniamy licznik z mianownikiem w drugim ułamku).

Przykład Dodawania Ułamków o Różnych Mianownikach: 1/3 + 1/4. NWW(3, 4) = 12. 1/3 = 4/12, 1/4 = 3/12. Zatem 1/3 + 1/4 = 4/12 + 3/12 = 7/12

Przykład Mnożenia Ułamków: 2/3 * 3/4 = (2 * 3) / (3 * 4) = 6/12 = 1/2 (po skróceniu)

Przykład Dzielenia Ułamków: 1/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4

Zadania Tekstowe: Przekładamy Słowa na Matematykę

Zadania tekstowe często sprawiają trudność, ale z odpowiednim podejściem można je rozwiązać! Oto kilka wskazówek:

Przeczytaj uważnie treść zadania. Zwróć uwagę na to, o co pytają.
Wypisz dane i szukane. To pomoże Ci uporządkować informacje.
Ustal, jakie działania trzeba wykonać. Zastanów się, co musisz obliczyć, żeby odpowiedzieć na pytanie.
Wykonaj obliczenia. Uważaj na jednostki!
Sprawdź, czy wynik ma sens. Czy odpowiedź jest logiczna w kontekście zadania?
Napisz odpowiedź. Odpowiedź powinna być pełnym zdaniem, odpowiadającym na pytanie zawarte w zadaniu.

Przykład: Ania ma 1/2 tabliczki czekolady, a Kasia ma 1/4 tabliczki czekolady. Ile tabliczki czekolady mają razem?

Rozwiązanie:

Dane: Ania - 1/2 tabliczki, Kasia - 1/4 tabliczki

Szukane: Ile tabliczki mają razem?

Działanie: 1/2 + 1/4 = 2/4 + 1/4 = 3/4

Odpowiedź: Ania i Kasia mają razem 3/4 tabliczki czekolady.

Praktyczne Wskazówki Przed Sprawdzianem

Rozwiąż jak najwięcej zadań z podręcznika "Matematyka z Plusem". Im więcej ćwiczysz, tym lepiej rozumiesz materiał.
Poproś o pomoc nauczyciela lub kolegę, jeśli czegoś nie rozumiesz. Nie wstydź się pytać!
Przejrzyj notatki z lekcji. Przypomnij sobie, co było omawiane na zajęciach.
Zrób sobie krótkie przerwy podczas nauki. Odpoczynek jest ważny!
Wyśpij się dobrze przed sprawdzianem. Wyspany umysł lepiej pracuje.
Na sprawdzianie czytaj uważnie polecenia. Zwróć uwagę na szczegóły.
Sprawdzaj swoje obliczenia. Unikniesz w ten sposób prostych błędów.
Nie panikuj! Jeśli nie wiesz, jak rozwiązać zadanie, przejdź do następnego i wróć do niego później.

Na Zakończenie: Matematyka Może Być Przyjemna!

Pamiętaj, że matematyka to nie tylko liczby i wzory. To także umiejętność logicznego myślenia i rozwiązywania problemów. Traktuj sprawdzian jako okazję do sprawdzenia swojej wiedzy i umiejętności, a nie jako karę. Wierzymy w Ciebie! Powodzenia na sprawdzianie!

Ten artykuł to tylko przypomnienie kluczowych zagadnień. Koniecznie zajrzyj do podręcznika "Matematyka z Plusem" i rozwiązuj zadania! Życzymy powodzenia!