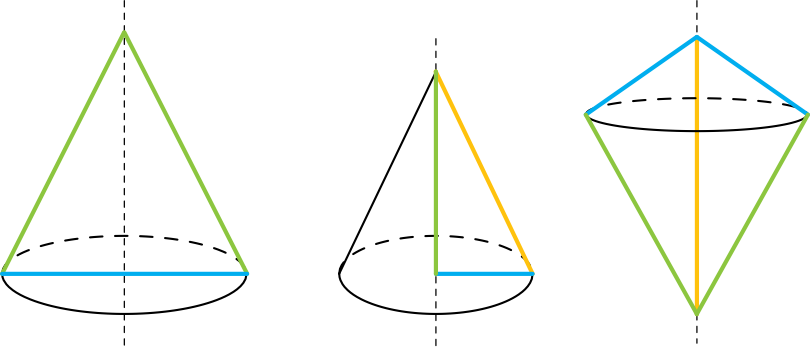Matematyka Bryły Obrotowe Gimnazjum Sprawdzian Gwo

Bryły obrotowe to figury geometryczne powstające przez obrót pewnej płaskiej figury wokół prostej. Wyobraź sobie, że bierzesz papierowy kształt i kręcisz nim bardzo szybko. Kształt, który utworzy się w powietrzu, to właśnie bryła obrotowa.

Najczęściej spotykane bryły obrotowe w szkole podstawowej i gimnazjum to: walec, stożek i kula.

Walec powstaje przez obrót prostokąta wokół jednego z jego boków. Wyobraź sobie puszkę konserwową. Jest to przykład walca. Dwie podstawy walca to koła, a powierzchnia boczna to prostokąt rozwinięty na płasko.

Kluczowe elementy walca to:

• Promień podstawy (r): Odległość od środka koła tworzącego podstawę do jego brzegu.
• Wysokość (h): Odległość między dwoma podstawami walca.

Stożek powstaje przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych. Pomyśl o lodach w wafelku w kształcie rożka. To jest stożek. Ma jedną podstawę w kształcie koła i wierzchołek.

Kluczowe elementy stożka to:

• Promień podstawy (r): Odległość od środka koła tworzącego podstawę do jego brzegu.
• Wysokość (h): Odległość od wierzchołka stożka do środka jego podstawy.
• Tworząca (l): Odcinek łączący wierzchołek stożka z punktem na brzegu jego podstawy. Jest to "przekątna" stożka.

Kula powstaje przez obrót koła lub półkola wokół jego średnicy. Piłka do nogi to najlepszy przykład kuli. Każdy punkt na powierzchni kuli jest tak samo daleko od jej środka.

Kluczowe elementy kuli to:

• Promień (r): Odległość od środka kuli do dowolnego punktu na jej powierzchni.

W kontekście sprawdzianów i zadań szkolnych, bardzo ważne jest umiejętność obliczania pól powierzchni i objętości tych brył.

Pole powierzchni całkowitej to suma pól wszystkich powierzchni bryły. Na przykład, dla walca jest to suma pól dwóch podstaw (kół) i pola powierzchni bocznej.

Objętość to miara przestrzeni, którą bryła zajmuje. Wyobraź sobie, ile wody można wlać do danego naczynia.

Przykładowe wzory, które mogą pojawić się na sprawdzianie:

• Objętość walca: V = π * r² * h
• Pole powierzchni bocznej walca: P_b = 2 * π * r * h
• Objętość stożka: V = (1/3) * π * r² * h
• Pole powierzchni kuli: P = 4 * π * r²
• Objętość kuli: V = (4/3) * π * r³

Pamiętaj, że litera π (pi) to stała matematyczna, która w przybliżeniu wynosi 3,14.

Rozumienie tych brył i ich właściwości jest kluczowe do rozwiązywania zadań. Ćwiczenie rysowania tych figur i stosowania wzorów pomoże Ci przygotować się do sprawdzianu z matematyki. Zwracaj uwagę na jednostki, w jakich podane są wymiary (np. centymetry) i w jakich mają być podane wyniki (np. centymetry kwadratowe dla pola, centymetry sześcienne dla objętości).