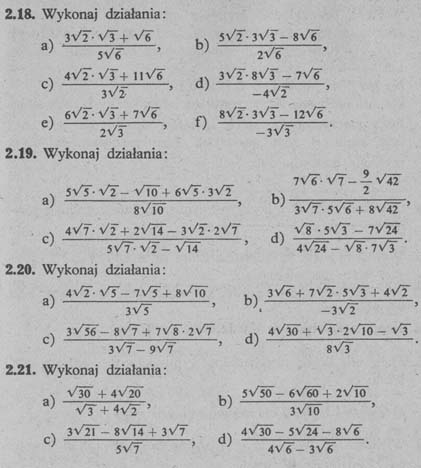Liczby Wymierne I Niewymierne Gimnazjum Sprawdzian

Czy kiedykolwiek czuliście ten znajomy ucisk w żołądku na myśl o klasówce z matematyki? Szczególnie gdy na horyzoncie pojawia się temat liczb wymiernych i niewymiernych? Spokojnie, nie jesteście sami. Dla wielu uczniów gimnazjum zrozumienie tej subtelnej różnicy może być prawdziwym wyzwaniem. Ten sprawdzian, choć może wydawać się przytłaczający, wcale nie musi być koszmarem. Wystarczy odrobina dobrego przygotowania, kilka kluczowych wskazówek i spojrzenie na ten temat z nieco innej perspektywy.

Pamiętajcie, że matematyka, choć czasem bywa abstrakcyjna, w rzeczywistości otacza nas wszędzie. Liczby, które poznajemy, mają swoje konkretne zastosowania, a zrozumienie ich natury pozwala nam lepiej pojmować świat. Dlatego właśnie dzisiejszy artykuł ma Wam pomóc nie tylko przygotować się do sprawdzianu z liczb wymiernych i niewymiernych, ale przede wszystkim oswoić ten temat i przekonać Was, że wcale nie jest on tak straszny, jak się wydaje.

Rozwikłać Tajemnicę: Czym Właściwie Są Liczby Wymierne i Niewymierne?

Zacznijmy od podstaw. Co właściwie kryje się pod tymi dwoma terminami? Wyobraźcie sobie, że wszystkie liczby, z którymi macie do czynienia, są jak pasażerowie w wielkiej podróży. Niektórzy z nich mają łatwe i przewidywalne trasy, inni zaś poruszają się po bardziej skomplikowanych ścieżkach.

Liczby Wymierne – Ci, Którzy Zawsze Znajdą Punkt Zapalny

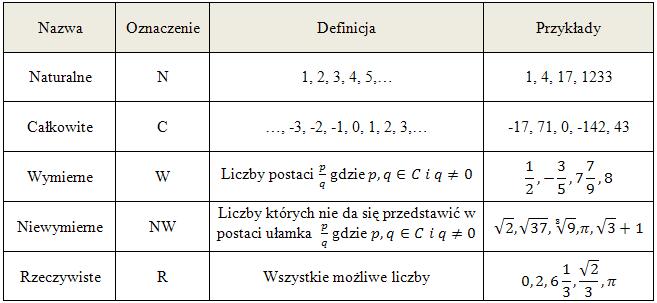
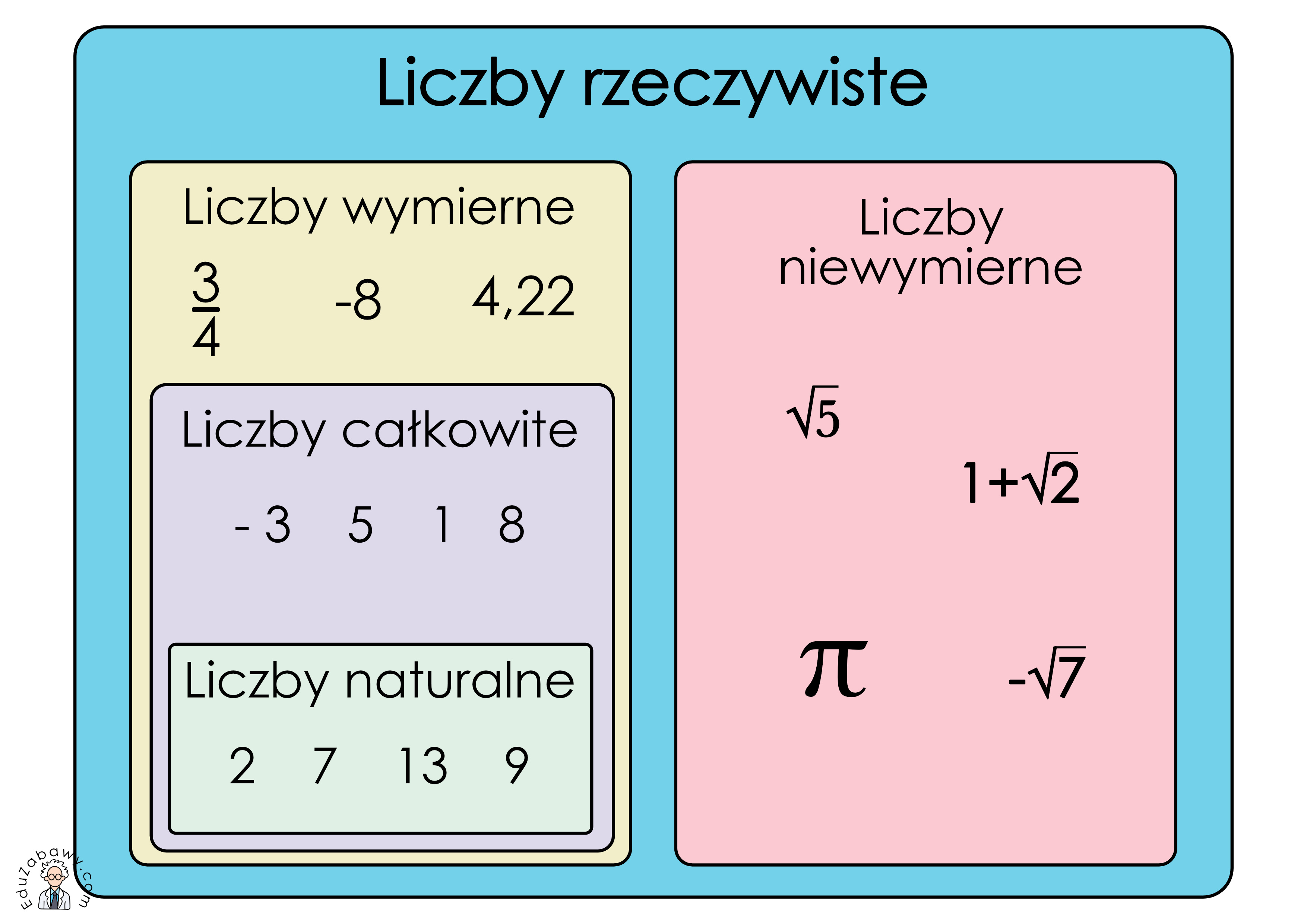
Liczby wymierne to te, które możemy zapisać w postaci ułamka zwykłego, gdzie licznik i mianownik są liczbami całkowitymi, a mianownik jest różny od zera. Brzmi znajomo? Oczywiście! To właśnie te liczby pojawiały się w zadaniach z ułamkami, proporcjami, procentami. Pomyślcie o tym jak o liczbach, które zawsze mają swoje konkretne, powtarzalne miejsce na osi liczbowej.

• Przykłady: 1/2, 3/4, -5/7, 0.75 (które można zapisać jako 75/100), 2 (które można zapisać jako 2/1), -3 (które można zapisać jako -3/1). Nawet liczby dziesiętne, które mają skończone rozwinięcie (np. 0.125) lub okresy (np. 0.333..., czyli 1/3), należą do tej grupy.

Kluczem do zrozumienia liczb wymiernych jest ich skończoność lub powtarzalność w zapisie dziesiętnym. Zawsze możemy określić, gdzie się zaczynają i gdzie kończą (jeśli są skończone), albo jaki jest ich cykl powtórzeń. To daje nam poczucie porządku i przewidywalności.

Liczby Niewymierne – Ci, Którzy Zaskakują Na Każdym Kroku

Teraz czas na tych bardziej tajemniczych pasażerów – liczby niewymierne. To liczby, których nie da się zapisać w postaci ułamka zwykłego, gdzie licznik i mianownik są liczbami całkowitymi. Ich zapis dziesiętny jest nieskończony i nieokresowy. Nigdy nie znajdziemy w nich powtarzającego się wzorca.

• Najsłynniejsze przykłady:
• Liczba Pi (π): Około 3.1415926535... To stosunek obwodu koła do jego średnicy. Jest to jedna z najbardziej rozpoznawalnych liczb niewymiernych, choć jej dokładna wartość nigdy nie zostanie w pełni poznana.
• Pierwiastki kwadratowe z liczb, które nie są kwadratami liczb całkowitych: Na przykład √2, √3, √5, √7. Pierwiastek z 2 jest pionierem w tej dziedzinie, jego przybliżona wartość to 1.4142135623...
• Liczba Eulera (e): Około 2.7182818284... Jest kluczowa w rachunku różniczkowym i całkowym oraz w teorii prawdopodobieństwa.

Zrozumienie liczb niewymiernych polega na uświadomieniu sobie, że ich nieskończony i nieprzewidywalny charakter sprawia, że są one odmienne od liczb wymiernych. Nie możemy ich „zamknąć” w prostym ułamku.

Dlaczego Ten Sprawdzian Jest Ważny? Praktyczne Zastosowania

Może się wydawać, że te abstrakcyjne pojęcia nie mają wiele wspólnego z codziennym życiem. Nic bardziej mylnego! Zrozumienie różnicy między liczbami wymiernymi a niewymiernymi jest fundamentem dla wielu zagadnień w matematyce, fizyce, inżynierii, a nawet w sztuce.

• Budownictwo i Architektura: W obliczeniach dotyczących konstrukcji, zwłaszcza przy projektowaniu łuków czy kopuł, często wykorzystuje się stałe takie jak Pi (liczba niewymierna).
• Fizyka: W wielu prawach fizyki, od mechaniki kwantowej po teorię względności, liczby niewymierne odgrywają kluczową rolę.
• Informatyka: Algorytmy, grafika komputerowa – wszędzie tam napotykamy na potrzebę precyzyjnych obliczeń, które często opierają się na liczbach wymiernych i niewymiernych.
• Finanse: Chociaż na co dzień operujemy głównie liczbami wymiernymi, bardziej zaawansowane modele finansowe mogą wykorzystywać również liczby niewymierne do opisu złożonych zjawisk.

Nawet w prostych sytuacjach, jak obliczanie powierzchni czy objętości przy użyciu konkretnych wzorów, często pojawia się konieczność pracy z liczbami, które mogą być niewymierne. Dlatego właśnie sprawdzian z tego zakresu ma na celu sprawdzenie Waszej zdolności do rozróżniania i pracy z tymi dwoma typami liczb.

Jak Przygotować Się do Sprawdzianu? Praktyczne Wskazówki

Teraz, gdy już wiemy, czym są liczby wymierne i niewymierne, przejdźmy do konkretów – jak skutecznie przygotować się do sprawdzianu i poradzić sobie z ewentualnymi trudnościami?

1. Powtórz Podstawy Ułamków i Rozwinięć Dziesiętnych

Bez solidnych podstaw będzie ciężko. Upewnijcie się, że rozumiecie:

• Jak zamieniać ułamki zwykłe na dziesiętne (skończone i okresowe).
• Jak zamieniać ułamki dziesiętne (skończone i okresowe) na zwykłe.
• Działania na ułamkach (dodawanie, odejmowanie, mnożenie, dzielenie).

Ćwiczenie czyni mistrza! Przeróbcie jak najwięcej zadań z zamiany ułamków, aby ta czynność stała się dla Was automatyczna.

2. Naucz się Rozpoznawać Liczby Niewymierne

Kluczem jest zapamiętanie kilku podstawowych przykładów liczb niewymiernych, takich jak Pi i pierwiastki z „niedoskonałych” kwadratów. Ale co, jeśli w zadaniu pojawi się nowa liczba? Oto kilka wskazówek:

• Próba zapisu jako ułamka: Jeśli dana liczba jest wynikiem operacji matematycznych, spróbujcie przekształcić ją tak, aby zobaczyć, czy da się ją zapisać w formie a/b.
• Rozwinięcie dziesiętne: Jeśli macie kalkulator (lub pamiętacie przybliżone wartości), sprawdźcie rozwinięcie dziesiętne. Jeśli jest nieskończone i nieokresowe, to mamy do czynienia z liczbą niewymierną.
• Pierwiastki: Pamiętajcie, że pierwiastek kwadratowy z liczby całkowitej jest niewymierny, jeśli ta liczba nie jest kwadratem liczby całkowitej. Np. √9 = 3 (liczba wymierna), ale √8 jest niewymierny.

3. Rozumiej Różnice, a Nie Tylko Zapamiętuj

Nie chodzi o ślepe zapamiętywanie definicji. Starajcie się zrozumieć istotę różnicy. Liczby wymierne mają „porządek” w swoim zapisie dziesiętnym (skończony lub powtarzający się). Liczby niewymierne są „chaotyczne” i nieprzewidywalne w nieskończoność.

Można to porównać do muzyki. Liczby wymierne to proste, powtarzalne melodie, które łatwo zapamiętać. Liczby niewymierne to złożone improwizacje, które ciągle nas zaskakują nowymi dźwiękami.

4. Ćwicz Rozwiązywanie Różnorodnych Zadań

Sprawdziany często zawierają zadania o różnym stopniu trudności. Przygotowując się, warto przerobić:

• Zadania typu „prawda/fałsz” dotyczące właściwości liczb wymiernych i niewymiernych.
• Zadania na klasyfikację liczb: Podana lista liczb, a Waszym zadaniem jest wskazanie, które są wymierne, a które niewymierne.
• Zadania z porównywaniem liczb: Która liczba jest większa – √3 czy 1.7? Tutaj często trzeba sprowadzić liczby do wspólnej postaci (np. dziesiętnej).
• Zadania wymagające obliczeń z wykorzystaniem liczb wymiernych i niewymiernych (np. obliczanie pola powierzchni prostokąta o bokach √2 i √8).

5. Zwróć Uwagę na Szczegóły i Formułowanie Odpowiedzi

Często punkty na sprawdzianie można stracić przez nieuwagę. Czytajcie polecenia bardzo dokładnie. Jeśli w zadaniu jest prośba o podanie odpowiedzi w postaci ułamka, a Wy podacie rozwinięcie dziesiętne (nawet dokładne), może to być uznane za błąd.

Podczas formułowania odpowiedzi, używajcie precyzyjnego języka matematycznego. Nie bójcie się napisać, że liczba jest niewymierna, ponieważ jej rozwinięcie dziesiętne jest nieskończone i nieokresowe.

Co Jeśli Nadal Czujesz Niepewność?

Nie martwcie się, jeśli po przeczytaniu tego artykułu nadal czujecie pewien niepokój. To normalne! Matematyka wymaga czasu i praktyki. Oto kilka dodatkowych kroków, które możecie podjąć:

• Poproś o pomoc nauczyciela: Wasz nauczyciel matematyki jest najlepszym źródłem wiedzy. Nie krępujcie się zadawać pytań na lekcji lub po niej.
• Pracuj z kolegami: Uczcie się razem! Tłumacząc sobie nawzajem materiał, utrwalacie wiedzę i odkrywacie nowe perspektywy.
• Korzystaj z dodatkowych materiałów: Istnieje wiele stron internetowych, filmów edukacyjnych (np. na YouTube) i aplikacji, które mogą pomóc Wam lepiej zrozumieć liczby wymierne i niewymierne.

Pamiętajcie, że sprawdzian to nie wyrok, a jedynie narzędzie do oceny Waszej aktualnej wiedzy. Celem jest nauka i rozwój. Każdy popełniony błąd jest okazją do wyciągnięcia wniosków i stania się lepszym w matematyce.

Trzymam za Was mocno kciuki! Wierzę, że z odpowiednim przygotowaniem poradzicie sobie na sprawdzianie z liczb wymiernych i niewymiernych śpiewająco!