Liczby Rzeczywiste Nowa Era Sprawdzian Wsrod Liczb

Czy kiedykolwiek zastanawialiście się nad tym, jak matematyka kształtuje świat wokół nas? Od precyzyjnych obliczeń inżynierów po złożone algorytmy stojące za naszymi ulubionymi aplikacjami, liczby rzeczywiste są fundamentem niemal każdej dziedziny nauki i technologii. W dzisiejszych czasach, gdy technologia rozwija się w zawrotnym tempie, zrozumienie tych podstawowych koncepcji staje się ważniejsze niż kiedykolwiek. Ten artykuł jest skierowany do uczniów, nauczycieli oraz wszystkich pasjonatów matematyki, którzy pragną pogłębić swoją wiedzę i przygotować się na wyzwania związane z nową erą edukacji matematycznej, w szczególności w kontekście sprawdzianów i testów sprawdzających zrozumienie liczb rzeczywistych.

Chcemy przedstawić Wam kompleksowy przegląd tego, co kryje się pod pojęciem liczb rzeczywistych, jak są one reprezentowane i jakie mają znaczenie w praktyce. Naszym celem jest nie tylko zaprezentowanie teorii, ale również pokazanie, jak przełożyć ją na praktyczne umiejętności, które są nieodzowne podczas rozwiązywania zadań, a zwłaszcza podczas pisania sprawdzianów, gdzie kluczowe jest precyzyjne i świadome używanie pojęć.

Nowa Era w Edukacji Matematycznej: Sprawdzian Wśród Liczb Rzeczywistych

Edukacja matematyczna przechodzi dynamiczną transformację. Tradycyjne metody nauczania ustępują miejsca podejściom bardziej interaktywnym i skoncentrowanym na praktycznym zastosowaniu wiedzy. W tym kontekście, sprawdziany z liczb rzeczywistych stają się nie tylko testem wiedzy teoretycznej, ale przede wszystkim weryfikacją zdolności do myślenia analitycznego i rozwiązywania problemów. Nowa era wymaga od nas nie tylko zapamiętywania definicji, ale przede wszystkim rozumienia głębokich zależności i umiejętności zastosowania narzędzi matematycznych w różnorodnych sytuacjach.

Współczesne sprawdziany często wykraczają poza proste zadania polegające na wykonaniu określonych operacji. Kładą nacisk na interpretację wyników, uzasadnianie swoich wyborów i łączność matematyki z rzeczywistością. Dlatego tak ważne jest, abyśmy mieli solidne podstawy w zakresie liczb rzeczywistych, które są kamieniem węgielnym całej matematyki i wielu dziedzin nauki.

Czym są Liczby Rzeczywiste? Podstawy i Zrozumienie

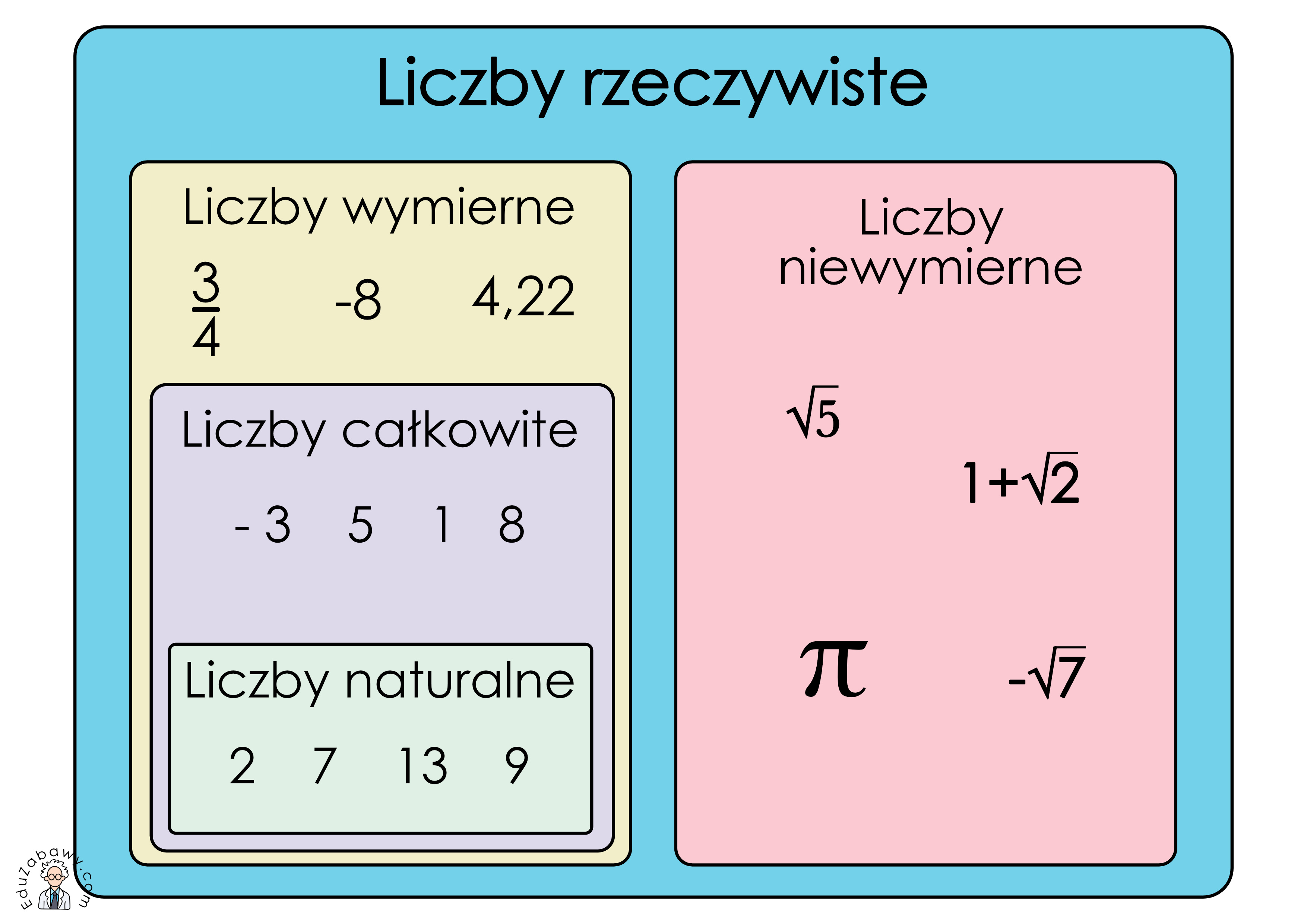
Na początek, wróćmy do samych korzeni. Czym właściwie są liczby rzeczywiste? W najprostszym ujęciu, są to wszystkie liczby, które można umieścić na osi liczbowej. Obejmują one zarówno liczby, które znamy z codziennego życia, jak i te bardziej abstrakcyjne, które jednak mają fundamentalne znaczenie w matematyce.

Możemy je podzielić na kilka głównych kategorii:

Liczby naturalne (N): To liczby, które służą do liczenia: 1, 2, 3, ... Czasami włączamy do nich również zero, co zależy od przyjętej konwencji. Są one najprostszym i najbardziej intuicyjnym typem liczb.
Liczby całkowite (Z): Oprócz liczb naturalnych, obejmują one również liczby przeciwne (ujemne) oraz zero: ..., -3, -2, -1, 0, 1, 2, 3, ... Pozwalają nam opisywać zadłużenia, temperatury poniżej zera czy inne sytuacje wymagające liczb ujemnych.
Liczby wymierne (Q): Są to liczby, które można przedstawić w postaci ułamka $\frac{a}{b}$, gdzie a jest liczbą całkowitą, a b jest niezerową liczbą całkowitą. Należą do nich m.in. ułamki zwykłe, dziesiętne okresowe i liczby całkowite. Przykłady to $\frac{1}{2}$, 0.75, $-\frac{3}{4}$. Wiele praktycznych pomiarów opiera się na liczbach wymiernych.
Liczby niewymierne (I): To liczby, których nie można przedstawić w postaci ułamka $\frac{a}{b}$. Mają one nieskończone, nieokresowe rozwinięcia dziesiętne. Najbardziej znanymi przykładami są $\pi$ (liczba pi) i $\sqrt{2}$ (pierwiastek z dwóch). Te liczby są niezbędne w geometrii, fizyce i analizie matematycznej.

Liczby rzeczywiste (R) są zatem sumą zbioru liczb wymiernych (Q) i niewymiernych (I). To pełen i spójny zbiór, który pozwala nam modelować praktycznie każdy obserwowalny fenomen w świecie fizycznym i matematycznym. Zrozumienie relacji między tymi podzbiorami jest kluczowe dla sukcesu na sprawdzianach.

Reprezentacja Liczb Rzeczywistych: Od Osi Liczbowej do Rozwinięć Dziesiętnych

Jednym z najbardziej intuicyjnych sposobów przedstawienia liczb rzeczywistych jest oś liczbowa. Jest to prosta linia, na której każdemu punktowi odpowiada dokładnie jedna liczba rzeczywista. Dzięki temu możemy wizualizować odległości między liczbami, ich porządek (która jest większa, która mniejsza) oraz odległość od zera (wartość bezwzględna).

Inną ważną formą reprezentacji są rozwinięcia dziesiętne. Jak wspomnieliśmy, liczby wymierne mają rozwinięcia dziesiętne skończone (np. 0.5, 1.25) lub okresowe (np. $0.333... = \frac{1}{3}$, $0.142857142857... = \frac{1}{7}$). Liczby niewymierne natomiast mają rozwinięcia dziesiętne nieskończone i nieokresowe, co jest ich charakterystyczną cechą.

Na sprawdzianach możemy spotkać się z zadaniami wymagającymi:

Konwersji między formami: Zamiana ułamka zwykłego na dziesiętny i odwrotnie.
Porównywania liczb: Określanie, która z dwóch liczb rzeczywistych jest większa lub mniejsza, często na podstawie ich rozwinięć dziesiętnych.
Szacowania wartości: Przybliżanie wartości liczb niewymiernych (np. $\pi \approx 3.14$, $\sqrt{2} \approx 1.41$).

Umiejętność sprawnego operowania tymi reprezentacjami jest fundamentalna. Pozwala nam to nie tylko rozwiązywać zadania, ale także lepiej rozumieć naturę liczb, z którymi pracujemy.

Właściwości Liczb Rzeczywistych: Podstawa Operacji Matematycznych

Zbiór liczb rzeczywistych, wraz z podstawowymi działaniami (dodawanie, odejmowanie, mnożenie, dzielenie), posiada szereg kluczowych właściwości, które definiują strukturę arytmetyki. Zrozumienie tych właściwości jest niezbędne do poprawnego rozwiązywania zadań, szczególnie tych bardziej złożonych, które często pojawiają się na sprawdzianach.

Do najważniejszych właściwości należą:

Przemienność i łączność dodawania i mnożenia:
- Przemienność dodawania: $a + b = b + a$
- Łączność dodawania: $(a + b) + c = a + (b + c)$
- Przemienność mnożenia: $a \cdot b = b \cdot a$
- Łączność mnożenia: $(a \cdot b) \cdot c = a \cdot (b \cdot c)$
Te właściwości pozwalają nam dowolnie przestawiać i grupować składniki lub czynniki, co ułatwia obliczenia.
Elementy neutralne:
- Element neutralny dodawania (zero): $a + 0 = a$
- Element neutralny mnożenia (jeden): $a \cdot 1 = a$
Ich istnienie jest kluczowe dla definicji odejmowania i dzielenia.
Elementy przeciwne i odwrotne:
- Element przeciwny do a: $-a$ ($a + (-a) = 0$)
- Element odwrotny do a (różnego od 0): $\frac{1}{a}$ ($a \cdot \frac{1}{a} = 1$)
Pozwalają nam definiować odejmowanie jako dodawanie elementu przeciwnego i dzielenie jako mnożenie przez element odwrotny.
Rozdzielność mnożenia względem dodawania: $a \cdot (b + c) = a \cdot b + a \cdot c$. To fundamentalna właściwość pozwalająca na upraszczanie wyrażeń algebraicznych i rozwiązywanie równań.
Porządek (nierówności): Dla dowolnych liczb rzeczywistych $a$ i $b$, zachodzi dokładnie jedna z relacji: $a < b$, $a = b$, $a > b$. Nierówności mają też swoje właściwości, np. dodanie tej samej liczby do obu stron nierówności nie zmienia jej znaku.

Na sprawdzianach często spotykamy zadania wymagające zastosowania tych właściwości do upraszczania skomplikowanych wyrażeń, rozwiązywania równań i nierówności, czy też dowodzenia pewnych twierdzeń. Świadomość tych praw jest warunkiem koniecznym do zrozumienia nawet najbardziej podstawowych operacji matematycznych.

Operacje na Liczbach Rzeczywistych: Praktyczne Zastosowania i Wyzwania

Zbiór liczb rzeczywistych umożliwia przeprowadzanie szerokiej gamy operacji, od prostych obliczeń arytmetycznych po bardziej zaawansowane zabiegi algebraiczne. Sprawdziany często weryfikują nasze umiejętności w tym zakresie, stawiając przed nami różnorodne zadania.

Podstawowe Działania Arytmetyczne

Dodawanie, odejmowanie, mnożenie i dzielenie to podstawowe narzędzia, które wykorzystujemy na co dzień. Kluczowe jest tutaj zachowanie kolejności działań oraz poprawne posługiwanie się liczbami ujemnymi i ułamkami.

Ułamki: Dodawanie i odejmowanie ułamków wymaga sprowadzania ich do wspólnego mianownika. Mnożenie ułamków jest prostsze – mnożymy liczniki i mianowniki. Dzielenie ułamków to mnożenie przez odwrotność dzielnika.
Pierwiastki: Działania na pierwiastkach wymagają znajomości ich właściwości, np. $\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$ czy $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$.

Potęgowanie i Logarytmowanie

Potęgowanie i logarytmowanie to operacje ściśle ze sobą powiązane. Potęgowanie pozwala nam szybko mnożyć tę samą liczbę przez siebie wielokrotnie, a logarytmowanie odpowiada na pytanie, do jakiej potęgi należy podnieść podstawę, aby otrzymać dany wynik.

Właściwości potęg: Należy znać i umieć stosować wzory takie jak $a^m \cdot a^n = a^{m+n}$, $\frac{a^m}{a^n} = a^{m-n}$, $(a^m)^n = a^{m \cdot n}$.
Właściwości logarytmów: Ważne są wzory typu $\log_b(x \cdot y) = \log_b(x) + \log_b(y)$, $\log_b(\frac{x}{y}) = \log_b(x) - \log_b(y)$, $\log_b(x^k) = k \cdot \log_b(x)$.

Te zagadnienia pojawiają się często w kontekście równań wykładniczych i logarytmicznych, które są typowymi zadaniami sprawdzającymi.

Wartość Bezwzględna

Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej. Jest zawsze nieujemna. $|a| = \begin{cases} a & \text{dla } a \ge 0 \\ -a & \text{dla } a < 0 \end{cases}$. Operacje z wartością bezwzględną wymagają szczególnej ostrożności i często prowadzą do rozpatrywania przypadków.

Wyzwania na sprawdzianach często wynikają z:

Połączenia różnych typów liczb: Zadania wymagające operowania jednocześnie na ułamkach, pierwiastkach i liczbach całkowitych.
Złożonych wyrażeń: Konieczność stosowania kolejności działań w wielopoziomowych wyrażeniach.
Niepełnego zrozumienia definicji: Błędy wynikające z nieuwagi przy operacjach na liczbach ujemnych czy wartości bezwzględnej.

Dlatego tak ważne jest, abyśmy systematycznie ćwiczyli te operacje, aby stały się one dla nas naturalne i bezproblemowe.

Liczby Rzeczywiste w Kontekście Sprawdzianu: Kluczowe Zagadnienia i Strategie

Pisanie sprawdzianu z liczb rzeczywistych to nie tylko test wiedzy, ale również próba strategicznego podejścia do rozwiązywania problemów. W nowej erze edukacji, gdzie liczy się nie tylko wynik, ale i proces jego uzyskania, warto znać kluczowe zagadnienia oraz skuteczne strategie przygotowawcze.

Najczęściej Sprawdzane Zagadnienia

Podczas sprawdzianów z liczb rzeczywistych, można spodziewać się zadań dotyczących:

Określania typu liczby: Czy dana liczba jest naturalna, całkowita, wymierna czy niewymierna.
Porównywania i porządkowania liczb: Ustawianie liczb w kolejności rosnącej lub malejącej, często na podstawie ich rozwinięć dziesiętnych lub obecności pierwiastków.
Operacji arytmetycznych na różnych typach liczb: Wykonywanie dodawania, odejmowania, mnożenia i dzielenia z udziałem ułamków, liczb dziesiętnych, pierwiastków.
Upraszczania wyrażeń algebraicznych: Zastosowanie właściwości działań i potęg do zredukowania skomplikowanych wyrażeń.
Rozwiązywania równań i nierówności: Zarówno prostych, jak i tych zawierających ułamki, potęgi czy wartości bezwzględne.
Szacowania i przybliżania wartości: Określanie przybliżonej wartości liczb niewymiernych lub wyników obliczeń.

Strategie Skutecznego Przygotowania

Aby osiągnąć sukces na sprawdzianie, warto wdrożyć kilka sprawdzonych strategii:

Zrozumienie podstaw: Nie ucz się na pamięć. Staraj się zrozumieć, dlaczego pewne reguły działają. Pytaj, gdy czegoś nie rozumiesz.
Systematyczne ćwiczenia: Rozwiązuj jak najwięcej różnorodnych zadań. Im więcej ćwiczysz, tym pewniej będziesz czuć się podczas sprawdzianu. Zacznij od prostych zadań, a stopniowo przechodź do trudniejszych.
Przegląd notatek i podręcznika: Regularnie powtarzaj definicje, wzory i przykłady. Zwróć uwagę na te fragmenty, które sprawiają Ci największą trudność.
Praca z poprzednimi sprawdzianami (jeśli dostępne): Analiza zadań z poprzednich testów pozwala zrozumieć styl nauczyciela i typy zadań, które są często sprawdzane.
Nauka efektywnego czytania poleceń: Dokładnie czytaj każde polecenie, zwracając uwagę na szczegóły i wymagania. Zaznaczaj kluczowe informacje.
Techniki rozwiązywania problemów: Kiedy napotkasz trudne zadanie, nie panikuj. Spróbuj rozłożyć je na mniejsze części, wykorzystaj znane Ci schematy rozwiązywania. Czasami warto odłożyć trudne zadanie na koniec i wrócić do niego, gdy będziesz mieć więcej czasu i świeży umysł.
Dbanie o precyzję obliczeń: Błędy rachunkowe są częstą przyczyną utraty punktów. Staraj się być dokładny i w miarę możliwości sprawdzać swoje obliczenia.

Pamiętajcie, że liczby rzeczywiste to nie tylko abstrakcyjny twór matematyczny. Są one narzędziem, które pozwala nam opisywać i rozumieć otaczający nas świat. Opanowanie ich tajników otwiera przed Wami nowe możliwości – zarówno w nauce, jak i w przyszłej karierze. Przygotowanie do sprawdzianu to inwestycja w Waszą przyszłość i możliwość pokazania, jak dobrze potraficie posługiwać się tym potężnym narzędziem.

Nowa era edukacji wymaga od nas aktywnego podejścia i ciągłego rozwoju. Mam nadzieję, że ten artykuł dostarczył Wam cennych informacji i strategii, które pomogą Wam z sukcesem zmierzyć się ze sprawdzianem z liczb rzeczywistych. Powodzenia!