Liczba Która Składa Się Z Całości I Ułamka

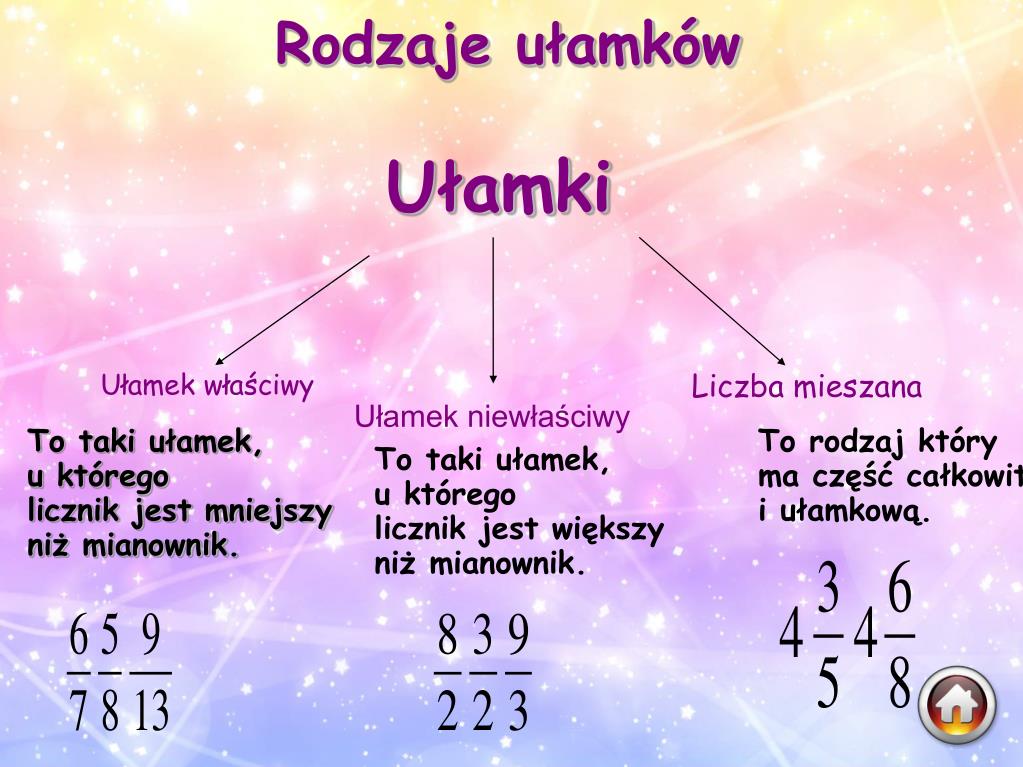
Liczba mieszana, zwana też liczbą zespoloną w pewnych kontekstach, to liczba, która składa się z dwóch podstawowych elementów: całości i ułamka właściwego. Mówiąc prościej, jest to sposób przedstawienia liczby większej od jedności przy pomocy liczby całkowitej i ułamka, którego licznik jest mniejszy od mianownika. Przykładowo, 3 1/2 (czytane "trzy i jedna druga") to liczba mieszana, gdzie 3 to część całkowita, a 1/2 to część ułamkowa.

Czym Jest Liczba Mieszana?

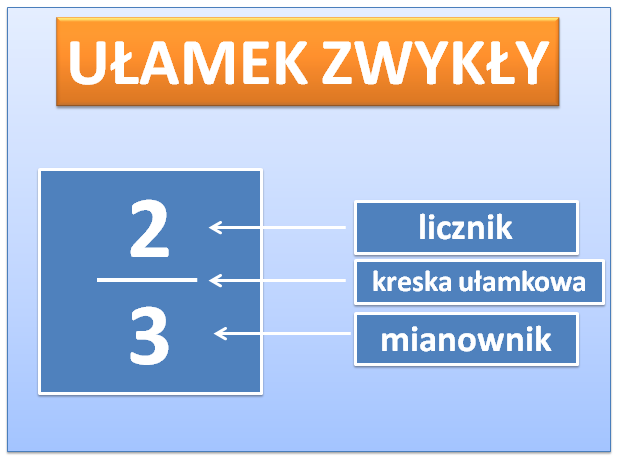
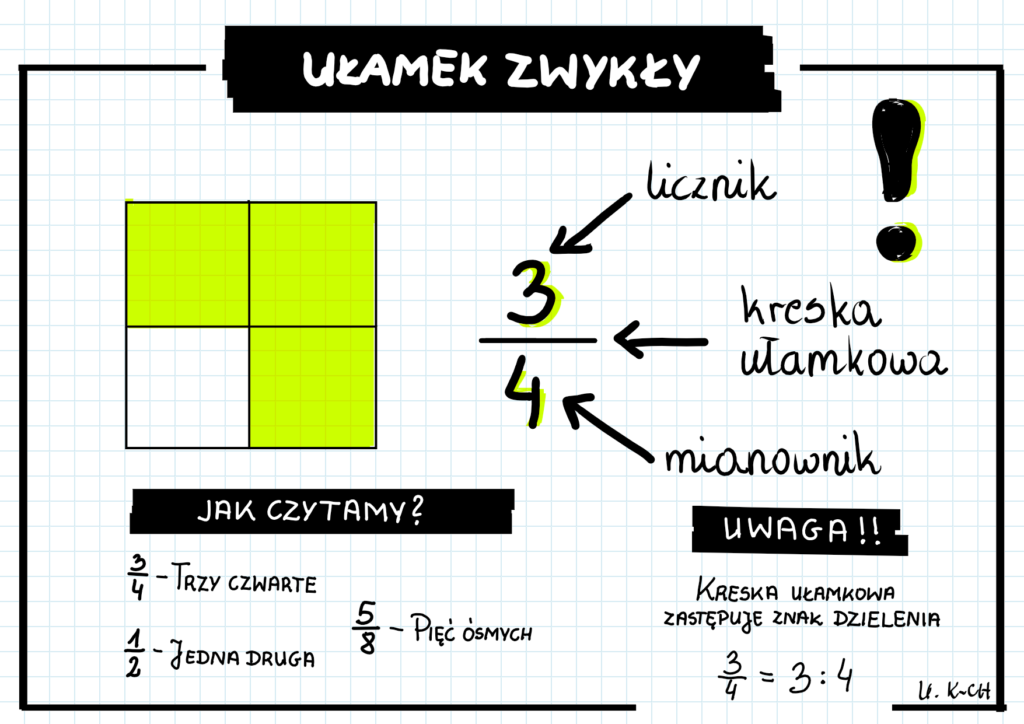
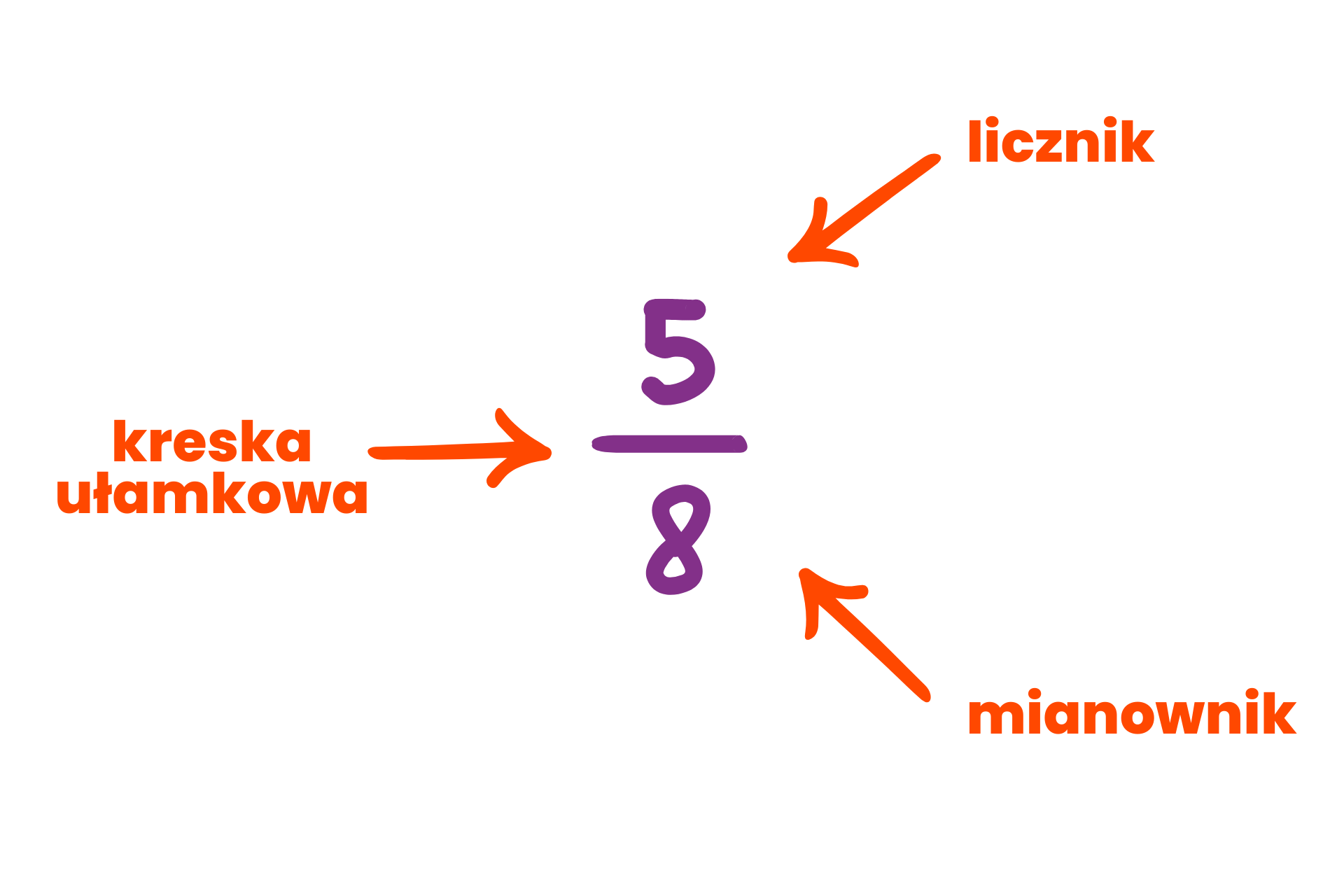
Liczba mieszana to reprezentacja liczby, która znajduje się między dwoma liczbami całkowitymi. Formalnie, można ją zdefiniować jako sumę liczby całkowitej i ułamka właściwego. Ułamek właściwy to taki, w którym licznik (liczba na górze) jest mniejszy od mianownika (liczba na dole). Dlaczego tak ważne jest, by ułamek był właściwy? Ponieważ, jeśli licznik jest większy lub równy mianownikowi, wówczas ułamek taki nazywamy niewłaściwym i można go przekształcić na liczbę mieszaną.

Rozważmy liczbę 5/3 (pięć trzecich). Jest to ułamek niewłaściwy. Możemy go przekształcić na liczbę mieszaną w następujący sposób: ile razy 3 mieści się w 5? Odpowiedź to 1. Zatem część całkowita naszej liczby mieszanej to 1. Ile zostaje reszty? 5 - (1 * 3) = 2. Zatem reszta, czyli 2, staje się licznikiem ułamka, a mianownik pozostaje ten sam, czyli 3. Ostatecznie otrzymujemy liczbę mieszaną 1 2/3 (jeden i dwie trzecie).

Dlaczego Liczby Mieszane Są Istotne?

Zrozumienie liczb mieszanych jest fundamentalne dla opanowania operacji na ułamkach i liczbami wymiernymi. Oto kilka kluczowych powodów:

• Ułatwiają Wizualizację: Liczby mieszane pozwalają na bardziej intuicyjne zrozumienie wielkości reprezentowanej przez ułamki. Widząc 3 1/2, łatwiej jest od razu ocenić, że jest to "trochę więcej niż 3", niż gdybyśmy mieli ułamek niewłaściwy 7/2.
• Praktyczne Zastosowania: W życiu codziennym często spotykamy się z sytuacjami, w których potrzebujemy używać liczb mieszanych. Przepisy kulinarne, pomiary, praca z czasem – to tylko kilka przykładów.
• Podstawa do Dalszej Nauki: Opanowanie liczb mieszanych jest niezbędne do zrozumienia bardziej zaawansowanych konceptów matematycznych, takich jak działania na ułamkach, proporcje i procenty.

Profesor Anna Kowalska, specjalizująca się w dydaktyce matematyki, podkreśla: "Liczby mieszane stanowią pomost między liczbami całkowitymi a ułamkami, umożliwiając uczniom głębsze zrozumienie relacji między nimi. Zaniedbanie tego tematu może skutkować trudnościami w dalszej nauce matematyki."

Jak Liczby Mieszane Wpływają na Uczniów?

Uczniowie często mają początkowo trudności z liczbami mieszanymi, ponieważ wymagają one zrozumienia zarówno liczb całkowitych, jak i ułamków. Częste problemy obejmują:

• Konwersja Między Ułamkami Niewłaściwymi a Liczbami Mieszanymi: Pomyłki w procesie dzielenia i wyznaczania reszty mogą prowadzić do błędnych wyników.
• Dodawanie i Odejmowanie Liczb Mieszanych: Wymaga to często znalezienia wspólnego mianownika dla ułamków, co bywa kłopotliwe.
• Mnożenie i Dzielenie Liczb Mieszanych: Najpierw trzeba je przekształcić na ułamki niewłaściwe, co dodatkowo komplikuje obliczenia.

Jednak odpowiednie metody nauczania mogą znacząco ułatwić zrozumienie tego tematu. Wykorzystanie wizualizacji (np. rysunków, diagramów), konkretnych przykładów z życia codziennego i stopniowe wprowadzanie trudniejszych zagadnień, pozwala na efektywne opanowanie liczb mieszanych.

Praktyczne Zastosowania w Szkole i w Życiu Ucznia

Oto kilka przykładów zastosowań liczb mieszanych, które mogą być bliskie uczniom:

• Gotowanie: Przepisy często podają ilości składników w postaci liczb mieszanych. Na przykład, przepis na ciasto może wymagać 2 1/4 szklanki mąki.
• Majsterkowanie: Podczas budowy karmnika dla ptaków, uczeń może potrzebować odmierzyć deskę o długości 1 1/2 metra.
• Sport: Wyniki sportowe często wyrażane są przy pomocy liczb mieszanych. Na przykład, biegacz przebiegł trasę w 12 3/4 minuty.
• Czas: Planowanie dnia, szacowanie ile czasu zajmie dana czynność, np. Uczenie się zajmie mi 2 1/2 godziny.

Dr. Jan Nowak, autor podręczników do matematyki, radzi: "Warto pokazywać uczniom, że matematyka nie jest oderwana od rzeczywistości. Użycie liczb mieszanych w kontekście, który jest dla nich zrozumiały i interesujący, może znacząco zwiększyć ich zaangażowanie i motywację do nauki."

"Najważniejsze jest, by uczniowie rozumieli, że liczby mieszane są po prostu innym sposobem zapisu liczb, z którymi już się spotkali. Kluczem do sukcesu jest budowanie solidnych fundamentów w postaci liczb całkowitych i ułamków." - Maria Zielińska, nauczycielka matematyki z wieloletnim doświadczeniem.

Podsumowując, liczby mieszane są ważnym elementem edukacji matematycznej. Zrozumienie ich istoty i praktyczne zastosowanie ułatwia uczniom rozwiązywanie problemów i rozwija umiejętność logicznego myślenia. Wykorzystanie odpowiednich metod nauczania, bazujących na wizualizacji i konkretnych przykładach, może przyczynić się do sukcesu w opanowaniu tego zagadnienia.