Hej uczniowie! Przygotowujecie się do sprawdzianu z liczb wymiernych? Nie martwcie się! Razem przejdziemy przez ten temat krok po kroku. Zobaczycie, że to nic trudnego.
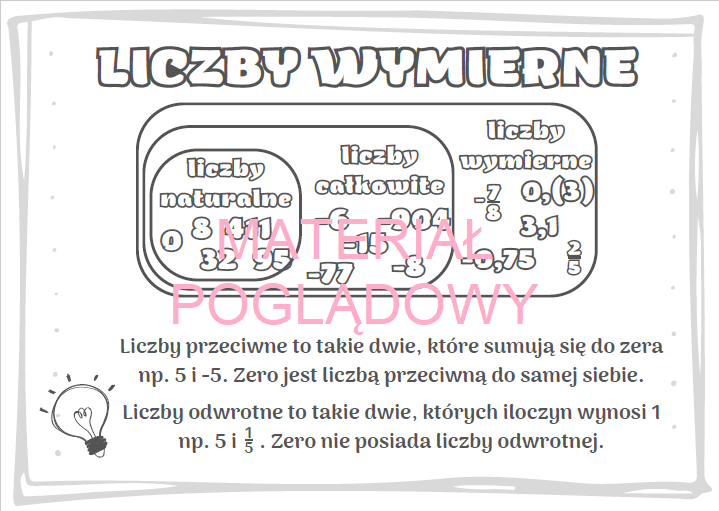
Czym właściwie są te liczby wymierne? Najprościej mówiąc, to każda liczba, którą można zapisać jako ułamek. Ułamek, czyli coś w postaci a/b, gdzie a i b to liczby całkowite, a b nie jest zerem. Ważne, żeby b nie było zerem, bo dzielenie przez zero jest niedozwolone!
Przykład? Proszę bardzo! Liczba 2 to liczba wymierna, bo możemy ją zapisać jako 2/1. Podobnie 0,5 to liczba wymierna, bo to inaczej 1/2. Nawet liczba -3 jest wymierna, bo to -3/1. Widzicie? To nie takie straszne.
Zastanówmy się, jakie liczby zaliczamy do liczb całkowitych. To liczby takie jak: ..., -3, -2, -1, 0, 1, 2, 3, ... Czyli wszystkie liczby bez ułamków i przecinków, zarówno dodatnie, jak i ujemne, oraz zero.
A liczby naturalne? To liczby całkowite dodatnie i zero. Czyli: 0, 1, 2, 3, 4, ... Pamiętajcie, że zero zalicza się do liczb naturalnych. Ważne, żeby to zapamiętać.
Dobra, mamy już pojęcie o liczbach wymiernych, całkowitych i naturalnych. Teraz czas na działania. Możemy dodawać, odejmować, mnożyć i dzielić liczby wymierne. Najważniejsze, to pamiętać o kolejności wykonywania działań: najpierw nawiasy, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie, a na końcu dodawanie i odejmowanie.
Dodawanie i odejmowanie ułamków wymaga sprowadzenia ich do wspólnego mianownika. Na przykład, jeśli chcemy dodać 1/2 i 1/3, musimy znaleźć wspólny mianownik. W tym przypadku będzie to 6. Zatem 1/2 to 3/6, a 1/3 to 2/6. Teraz możemy dodać: 3/6 + 2/6 = 5/6.
Mnożenie ułamków jest prostsze. Mnożymy licznik przez licznik i mianownik przez mianownik. Na przykład, 1/2 * 1/3 = 1/6. Pamiętajcie tylko, żeby przed mnożeniem spróbować skrócić ułamki, jeśli się da. To ułatwi obliczenia.
Dzielenie ułamków to tak naprawdę mnożenie przez odwrotność drugiego ułamka. Czyli, jeśli chcemy podzielić 1/2 przez 1/3, to mnożymy 1/2 przez 3/1 (odwrotność 1/3). Wynik to 3/2.
Ułamki dziesiętne też są liczbami wymiernymi. Możemy je zamienić na ułamki zwykłe i odwrotnie. Na przykład, 0,75 to 3/4. A ułamek 1/4 to 0,25. Ważne, żeby umieć to robić sprawnie.
Pamiętajcie o liczbach mieszanych! To liczby składające się z części całkowitej i ułamkowej, np. 2 1/2. Przed wykonywaniem działań, warto zamienić je na ułamki niewłaściwe (np. 2 1/2 = 5/2).
Powodzenia na sprawdzianie! Pamiętajcie o spokojnym czytaniu zadań i dokładnym wykonywaniu obliczeń. Pamiętajcie, że praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie liczby wymierne.