Drodzy nauczyciele matematyki, ten artykuł poświęcony jest zagadnieniom kątów wpisanych i środkowych w okręgu. Przygotowanie sprawdzianu z tej tematyki może być wyzwaniem. Omówimy metody skutecznego nauczania tego materiału.
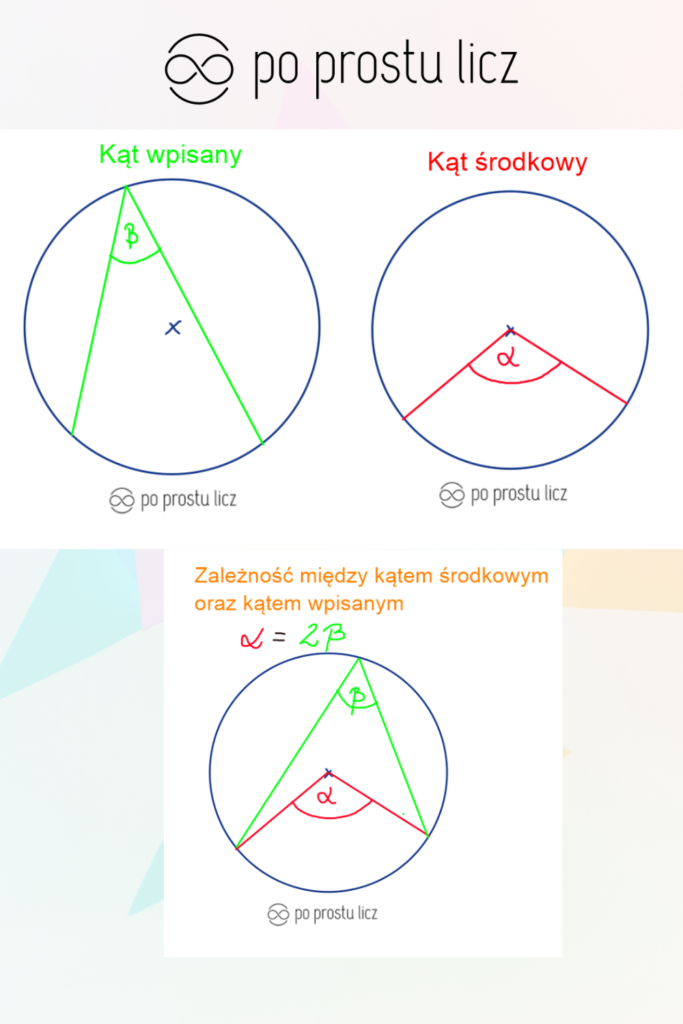
Zacznijmy od podstaw. Kąt środkowy to kąt, którego wierzchołek leży w środku okręgu. Jego ramiona przecinają okrąg w dwóch punktach. Miarą kąta środkowego jest miara łuku, na którym jest on oparty. Zapamiętajmy definicję, pomoże ona w dalszej pracy.
Kąt wpisany ma wierzchołek na okręgu. Ramiona takiego kąta również przecinają okrąg. Miara kąta wpisanego jest równa połowie miary kąta środkowego opartego na tym samym łuku. To kluczowa relacja, którą uczniowie muszą opanować.
Wyjaśniając te pojęcia, używajmy wizualizacji. Rysujmy różne okręgi z kątami. Zaznaczajmy łuki, na których są oparte kąty. Użycie kolorów do rozróżnienia kątów i łuków ułatwia zrozumienie.
Częstym błędem jest mylenie kąta wpisanego ze środkowym. Uczniowie zapominają o relacji "połowy" miary. Podkreślajmy wielokrotnie związek między miarami tych kątów. Ćwiczenia z obliczaniem miar, znając miarę drugiego kąta, są niezbędne.
Innym problemem jest identyfikacja łuku, na którym oparty jest kąt. Upewnijmy się, że uczniowie rozumieją, które punkty na okręgu wyznaczają ten łuk. Proponujmy różne położenia kątów, aby sprawdzić ich zrozumienie. Niech uczniowie sami rysują i oznaczają łuki.
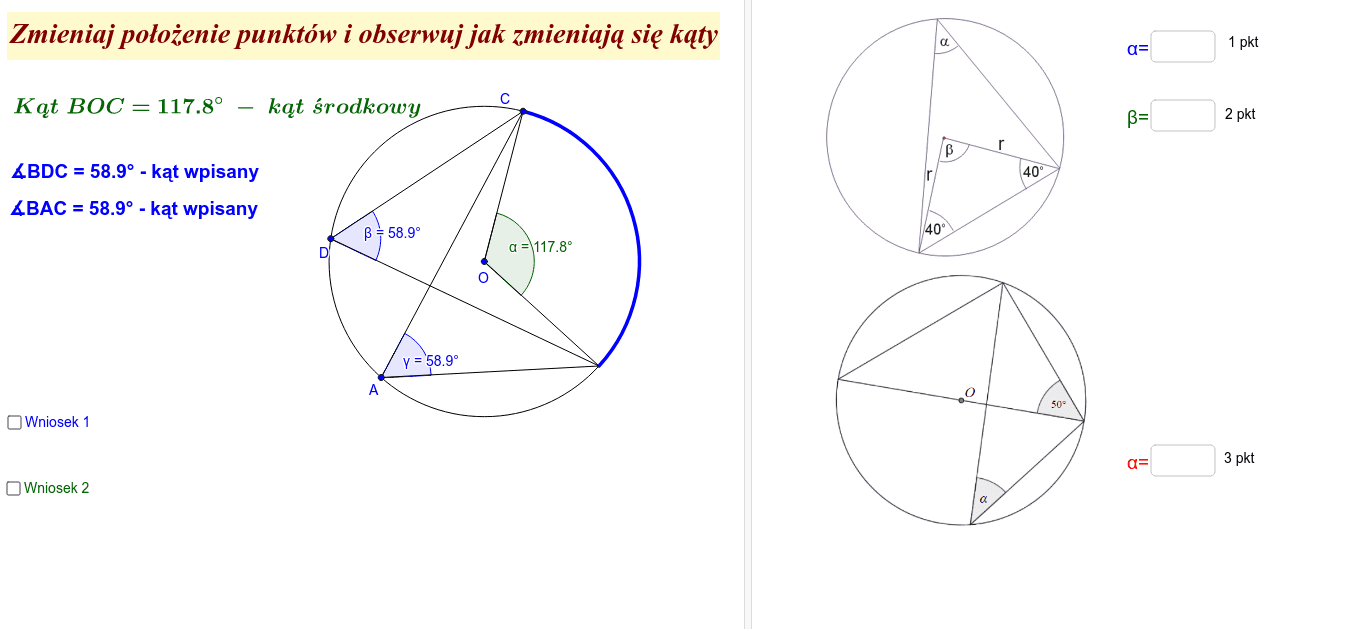
Jak uatrakcyjnić lekcję? Wykorzystajmy interaktywne programy do geometrii. Pozwalają one na dynamiczne przesuwanie wierzchołków kątów i obserwowanie zmian miar. Możemy też zorganizować konkurs rysunkowy. Uczniowie rysują okręgi z różnymi kątami i rozwiązują zadania.
Sprawdzian powinien zawierać zadania różnego typu. Obliczanie miar kątów znając inne kąty. Określanie, czy kąt jest wpisany, czy środkowy. Znajdowanie miary łuku na podstawie kąta. Zadania otwarte, wymagające uzasadnienia odpowiedzi, również są wartościowe.
Dodatkowo, w sprawdzianie warto uwzględnić zadania praktyczne. Na przykład, rysowanie okręgu, kąta środkowego i wpisanego. Uczniowie powinni pokazać, że rozumieją definicje i potrafią je zastosować w praktyce.
Pamiętajmy o regularnym powtarzaniu materiału. Kąty wpisane i środkowe pojawiają się w wielu innych zagadnieniach geometrii. Utrwalanie wiedzy jest kluczowe dla sukcesu uczniów.
Podsumowując, nauczanie o kątach wpisanych i środkowych wymaga cierpliwości i użycia różnorodnych metod. Wizualizacja, ćwiczenia i interaktywne narzędzia pomagają w zrozumieniu. Dobrze przygotowany sprawdzian oceni wiedzę i umiejętności uczniów.