Kąty Proste Ostre I Rozwarte Sprawdzian Klasa 5

Zrozumienie kątów to fundamentalny element nauki geometrii, który ma ogromne znaczenie dla rozwoju logicznego myślenia i umiejętności rozwiązywania problemów przestrzennych. W piątej klasie szkoły podstawowej uczniowie stykają się z podstawowymi typami kątów: kątem prostym, kątem ostrym i kątem rozwartym. Precyzyjne opanowanie tych pojęć jest kluczowe dla dalszej edukacji matematycznej, a także dla postrzegania świata wokół nas, gdzie kąty odgrywają nieocenioną rolę.

Kąt Prosty, Ostry i Rozwarty – Podstawy Geometrii dla Piątoklasistów

W świecie geometrii, kąt jest pojęciem podstawowym, definiującym wzajemne położenie dwóch prostych lub półprostych wychodzących ze wspólnego punktu, zwanego wierzchołkiem. W cinquième klasie szkoły podstawowej uczniowie poznają trzy główne typy kątów, które różnią się od siebie miarą:

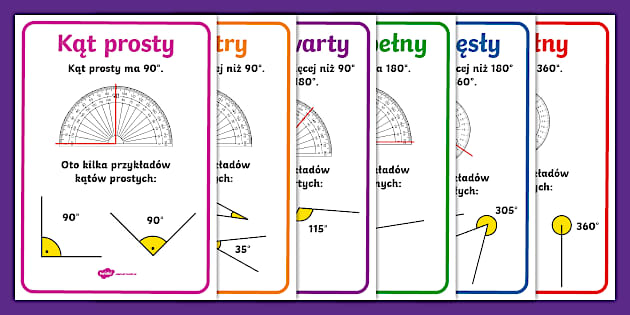
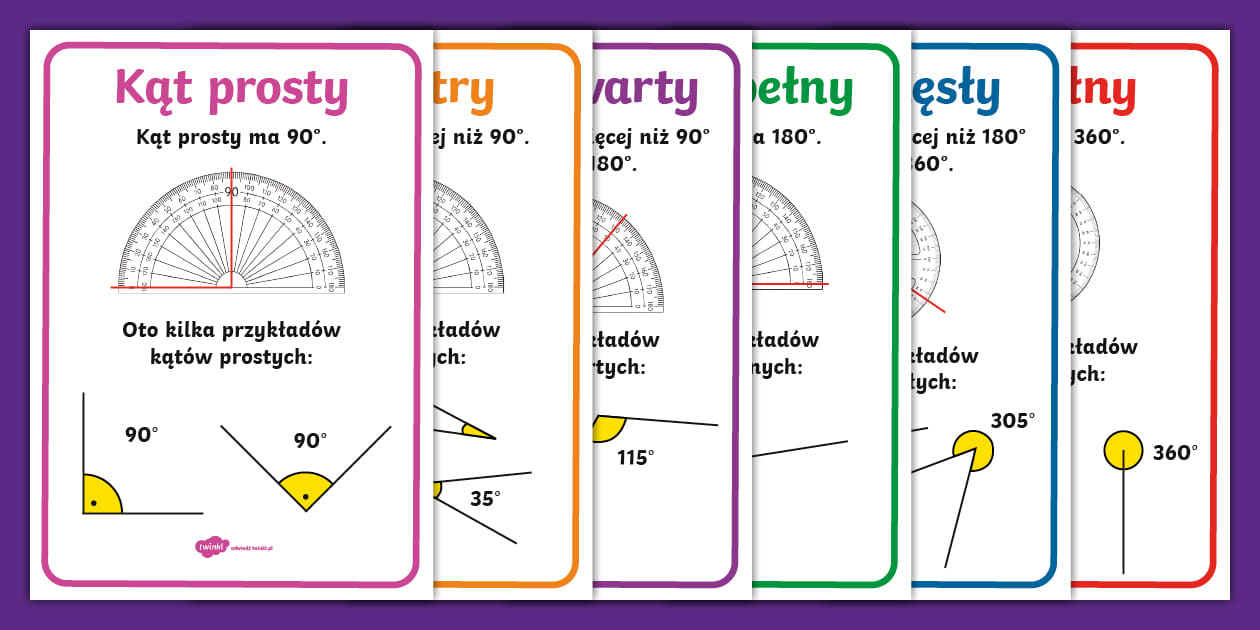
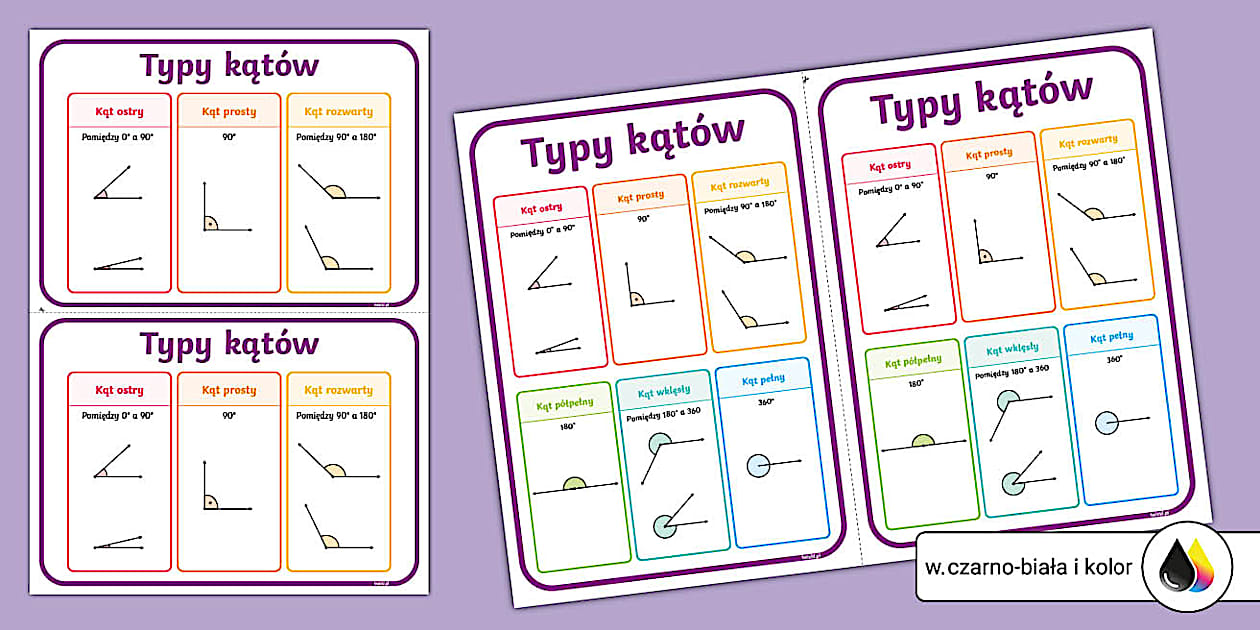
Kąt prosty: Jest to kąt, którego miara wynosi dokładnie 90 stopni. Jego charakterystyczny kształt przypomina literę "L" i jest on wszechobecny w otaczającej nas rzeczywistości. Kąt prosty jest punktem odniesienia dla innych kątów.
Kąt ostry: To kąt, którego miara jest mniejsza niż 90 stopni, ale większa niż 0 stopni. Im mniejszy kąt ostry, tym bardziej "ściśnięty" jest jego kształt.
Kąt rozwarty: Charakteryzuje się miarą większą niż 90 stopni, ale mniejszą niż 180 stopni. Kąt rozwarty jest "szerzej otwarty" niż kąt prosty.

Rozróżnianie i rozumienie tych typów kątów jest nie tylko ćwiczeniem umysłowym, ale także przygotowaniem do bardziej zaawansowanych zagadnień geometrycznych, takich jak trójkąty, czworokąty czy figury przestrzenne.

Dlaczego Znajomość Kątów Jest Ważna?

Nauka o kątach prostych, ostrych i rozwartych w piątej klasie nie jest celem samym w sobie. Jest to budowanie fundamentów, które procentują w wielu obszarach życia i nauki. Zrozumienie tych podstawowych zależności geometrycznych:

Rozwija umiejętności przestrzenne: Dzieci uczą się postrzegać i analizować kształty oraz relacje między nimi w przestrzeni. To kluczowe dla takich dziedzin jak rysunek techniczny, architektura czy projektowanie.
Wzmacnia logiczne myślenie: Klasyfikacja kątów wymaga od ucznia umiejętności porównywania, kategoryzowania i stosowania określonych kryteriów. Jest to trening dla umysłu, który przekłada się na lepsze radzenie sobie z problemami w różnych dziedzinach.
Ułatwia naukę kolejnych zagadnień matematycznych: Kąty są obecne w niemal każdym aspekcie geometrii. Bez solidnego zrozumienia podstaw, dalsze lekcje matematyki mogą stać się przytłaczające.
Pomaga w rozumieniu świata: Wiele obiektów i zjawisk w naszym otoczeniu opiera się na zasadach geometrii. Od konstrukcji budynków, przez pracę narzędzi, po ruch planet – wszędzie tam występują kąty.

Jak podkreśla wielu pedagogów, wczesne zetknięcie z pojęciami geometrycznymi, podanymi w przystępny sposób, kształtuje w uczniach pozytywne nastawienie do matematyki. Cytując profesora matematyki, dr hab. Jana Kowalskiego: "Fundamentalne pojęcia, takie jak kąt prosty, ostry i rozwarty, jeśli zostaną dobrze zrozumiane na etapie szkoły podstawowej, stanowią solidny filar dla dalszego rozwoju kompetencji matematycznych i przestrzennych ucznia. To inwestycja, która przynosi długoterminowe korzyści edukacyjne."

Wpływ na Uczniów: Od Lęku do Zrozumienia

Dla wielu piątoklasistów, sprawdzian z kątów prostych, ostrych i rozwartych może być źródłem stresu, zwłaszcza jeśli pojawiają się trudności w ich odróżnianiu. Kluczem do sukcesu jest tutaj odpowiednie podejście dydaktyczne. Metody nauczania, które wykorzystują wizualizację, praktyczne ćwiczenia i odniesienia do życia codziennego, znacząco zmniejszają barierę w zrozumieniu tych pojęć. Uczniowie, którzy widzą praktyczne zastosowania kątów, są bardziej zmotywowani do nauki i chętniej angażują się w zadania.

Kiedy uczeń potrafi samodzielnie zidentyfikować kąt prosty w rogu pokoju, kąt ostry w zagiętej kartce papieru czy kąt rozwarty w rozłożonym wachlarzu, pojawia się poczucie zrozumienia i sprawczości. To buduje pewność siebie i zmniejsza obawy przed matematyką jako przedmiotem trudnym i abstrakcyjnym. Zamiast skupiać się na zapamiętywaniu definicji, uczniowie zaczynają dostrzegać logikę i porządek w otaczającym ich świecie.

Praktyczne Zastosowania Kątów w Szkole i w Życiu

Pojęcia kątów prostych, ostrych i rozwartych mają liczne zastosowania, które uczniowie piątej klasy mogą dostrzec na co dzień:

W szkole:

Na lekcjach plastyki i techniki: Tworzenie modeli, rysowanie perspektywiczne czy konstruowanie prostych przedmiotów często wymaga precyzyjnego odmierzenia kątów.
Na lekcjach matematyki: Rozpoznawanie kątów w figurach geometrycznych, mierzenie ich za pomocą kątomierza, budowanie figur o określonych kątach – to standardowe ćwiczenia.
W nauce o świecie: Opisywanie kształtów obiektów, rozumienie map i planów, a nawet rozumienie zasad działania prostych mechanizmów.

W życiu codziennym:

Architektura i budownictwo: Narożniki ścian tworzą kąty proste, pochylenie dachu to kąt ostry lub rozwarty. Budowanie jest procesem opartym na geometrii.
Meble i wyposażenie: Kształt stołu, krzesła, szafki – wszystko to zawiera kąty, które decydują o ich funkcjonalności i estetyce.
Narzędzia i urządzenia: Kątomierz, ekierka, ramię dźwigu, mechanizmy otwierania drzwi czy okien – w ich konstrukcji kluczową rolę odgrywają kąty.
Sport: Kąt rzutu do kosza, kąt uderzenia piłki tenisowej, nachylenie stoku narciarskiego – wszystkie te aspekty mają wymiar geometryczny.
Nawigacja: Ustalanie kierunków, czytanie map, zrozumienie wskazań kompasu – wymaga to umiejętności pracy z kątami.

Jak zauważają autorzy podręczników i materiałów dydaktycznych dla klas piątych, największą satysfakcję sprawia uczniom dostrzeganie tych związków w świecie realnym. Kiedy dziecko potrafi wskazać kąt prosty w monitorze komputera lub kąt ostry w ramionach roweru, matematyka staje się dla niego żywa i zrozumiała. Jest to proces, który buduje nie tylko wiedzę, ale także pewność siebie i otwartość na dalszą naukę.

Podsumowując, sprawdzian z kątów prostych, ostrych i rozwartych dla klasy piątej to test nie tylko wiedzy teoretycznej, ale także umiejętności zastosowania tych podstawowych pojęć w praktyce. Dobre przygotowanie do tego sprawdzianu, oparte na zrozumieniu, a nie tylko na pamięciowym opanowaniu definicji, otwiera uczniom drzwi do fascynującego świata geometrii i rozwija ich kluczowe kompetencje na przyszłość.