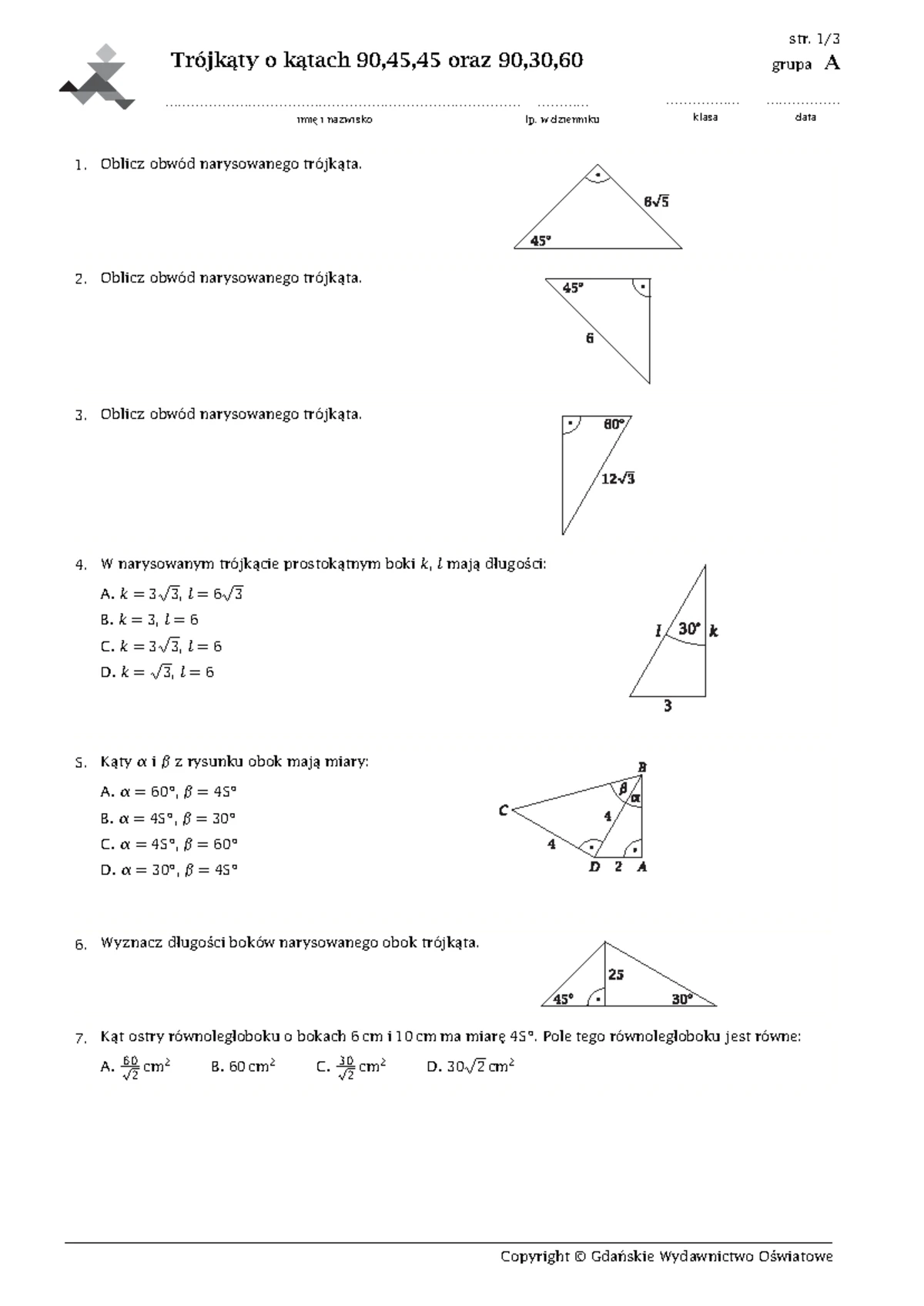
Katy I Trojkaty Sprawdzian Klasa 8

Kąty i Trójkąty – Sprawdzian Klasa 8 to zestaw zagadnień, z którymi uczeń klasy 8 powinien być zaznajomiony w kontekście geometrii. Obejmuje on przede wszystkim wiedzę na temat własności kątów oraz rodzajów i cech trójkątów, a także umiejętność rozwiązywania zadań związanych z nimi.

1. Kąty: Definicje i Własności

Zaczynamy od kątów. Ważne jest, aby rozróżniać kąty proste (90°), ostre (mniejsze niż 90°), rozwarte (większe niż 90°, a mniejsze niż 180°) i półpełne (180°). Pamiętaj o kątach wierzchołkowych (równe miary) i przyległych (suma miar to 180°).

Przykład: Dwie proste przecinają się, tworząc kąt o mierze 60°. Kąt wierzchołkowy do niego również ma 60°. Kąt przyległy do niego ma miarę 180° - 60° = 120°.

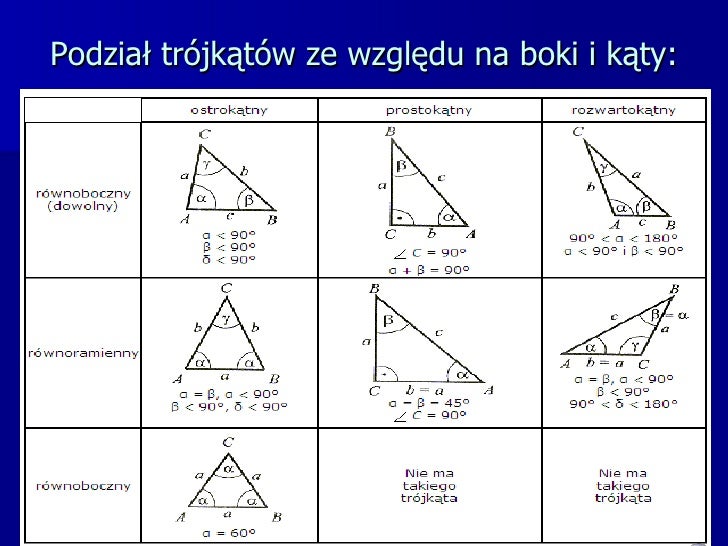
2. Rodzaje Trójkątów

Trójkąty dzielimy ze względu na kąty: ostrokątne (wszystkie kąty ostre), prostokątne (jeden kąt prosty) i rozwartokątne (jeden kąt rozwarty). Ze względu na boki wyróżniamy równoboczne (wszystkie boki równe, wszystkie kąty 60°), równoramienne (dwa boki równe, dwa kąty przy podstawie równe) i różnoboczne (wszystkie boki różne).

Przykład: Trójkąt o bokach 3 cm, 4 cm i 5 cm jest trójkątem prostokątnym (spełnia twierdzenie Pitagorasa: 3² + 4² = 5²), a jednocześnie jest różnoboczny.

3. Suma Kątów w Trójkącie

Suma kątów w każdym trójkącie wynosi 180°. To podstawowa zasada, którą wykorzystujemy do obliczania brakujących kątów.

Przykład: W trójkącie dwa kąty mają miary 40° i 60°. Trzeci kąt ma miarę 180° - 40° - 60° = 80°.

4. Twierdzenie Pitagorasa

Twierdzenie Pitagorasa dotyczy tylko trójkątów prostokątnych i mówi, że suma kwadratów długości przyprostokątnych (a i b) jest równa kwadratowi długości przeciwprostokątnej (c): a² + b² = c².

Przykład: Przyprostokątne trójkąta prostokątnego mają długości 6 cm i 8 cm. Długość przeciwprostokątnej wynosi √(6² + 8²) = √(36 + 64) = √100 = 10 cm.

5. Wysokości w Trójkącie

Wysokość trójkąta to odcinek opuszczony prostopadle z wierzchołka na przeciwległy bok (lub jego przedłużenie). W każdym trójkącie mamy trzy wysokości.

Przykład: W trójkącie równobocznym wszystkie wysokości są równe i przecinają się w jednym punkcie, który jest środkiem ciężkości trójkąta.

Praktyczne Zastosowania:

Wiedza o kątach i trójkątach jest niezbędna w wielu dziedzinach. Po pierwsze, w architekturze i budownictwie, gdzie precyzyjne obliczenia kątów i wymiarów są kluczowe dla stabilności i estetyki budowli. Po drugie, w nawigacji, gdzie znajomość trójkątów i ich właściwości pozwala na określanie pozycji i wyznaczanie tras.