Kąty w Trójkątach to zagadnienie z geometrii, które omawia relacje między kątami wewnętrznymi trójkąta. Sprawdzian Klasa 7 z tego materiału zazwyczaj sprawdza zrozumienie tych zależności i umiejętność ich wykorzystania w rozwiązywaniu zadań.
Krok 1: Suma Kątów w Trójkącie
Podstawowa zasada: Suma miar kątów wewnętrznych w każdym trójkącie wynosi 180 stopni. Oznacza to, że jeśli mamy trójkąt ABC, to kąt A + kąt B + kąt C = 180°.
Przykład: Jeśli kąt A ma 60°, a kąt B ma 80°, to kąt C = 180° - 60° - 80° = 40°.
Krok 2: Rodzaje Trójkątów
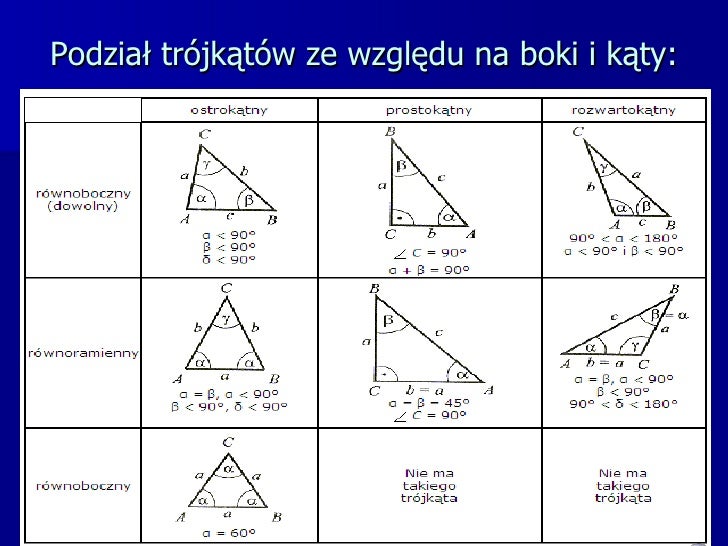
Rozróżniamy trójkąty ze względu na miary ich kątów i długości boków:
- Trójkąt Ostrokątny: Wszystkie kąty są ostre (mniejsze niż 90°).
- Trójkąt Prostokątny: Jeden kąt jest prosty (90°). Dwa pozostałe kąty są ostre i ich suma wynosi 90°.
- Trójkąt Rozwartokątny: Jeden kąt jest rozwarty (większy niż 90°).
- Trójkąt Równoboczny: Wszystkie boki są równe, a wszystkie kąty mają po 60°.
- Trójkąt Równoramienny: Dwa boki są równe. Kąty przy podstawie (czyli boku, który nie jest ramieniem) są równe.
- Trójkąt Różnoboczny: Wszystkie boki mają różne długości, a wszystkie kąty mają różne miary.
Przykład: W trójkącie prostokątnym, jeśli jeden z kątów ostrych ma 30°, to drugi kąt ostry ma 90° - 30° = 60°.
Krok 3: Kąty Przyległe do Boku
W trójkącie równoramiennym, kąty leżące naprzeciwko równych boków są równe. Jeśli trójkąt ABC jest równoramienny z AB = AC, to kąt B = kąt C.
Przykład: W trójkącie równoramiennym, kąt między ramionami (kąt A) ma 100°. Wtedy kąty przy podstawie (kąty B i C) mają (180° - 100°) / 2 = 40° każdy.
Krok 4: Kąt Zewnętrzny Trójkąta
Kąt zewnętrzny trójkąta jest równy sumie dwóch kątów wewnętrznych nieprzyległych do niego. Jeśli kąt zewnętrzny leży przy wierzchołku A, to jego miara jest równa kątowi B + kątowi C.
Przykład: Jeśli w trójkącie ABC kąt B = 50° i kąt C = 70°, to kąt zewnętrzny przy wierzchołku A (przyległy do kąta A) ma miarę 50° + 70° = 120°.
Dlaczego to jest ważne?
- Architektura i Inżynieria: Zrozumienie relacji kątów w trójkątach jest kluczowe w projektowaniu budynków, mostów i innych konstrukcji. Zapewnia to stabilność i wytrzymałość konstrukcji.
- Nawigacja: W nawigacji, szczególnie w lotnictwie i żegludze, wykorzystuje się trigonometrię, która bazuje na zależnościach kątowych w trójkątach, aby określić pozycję i kurs.