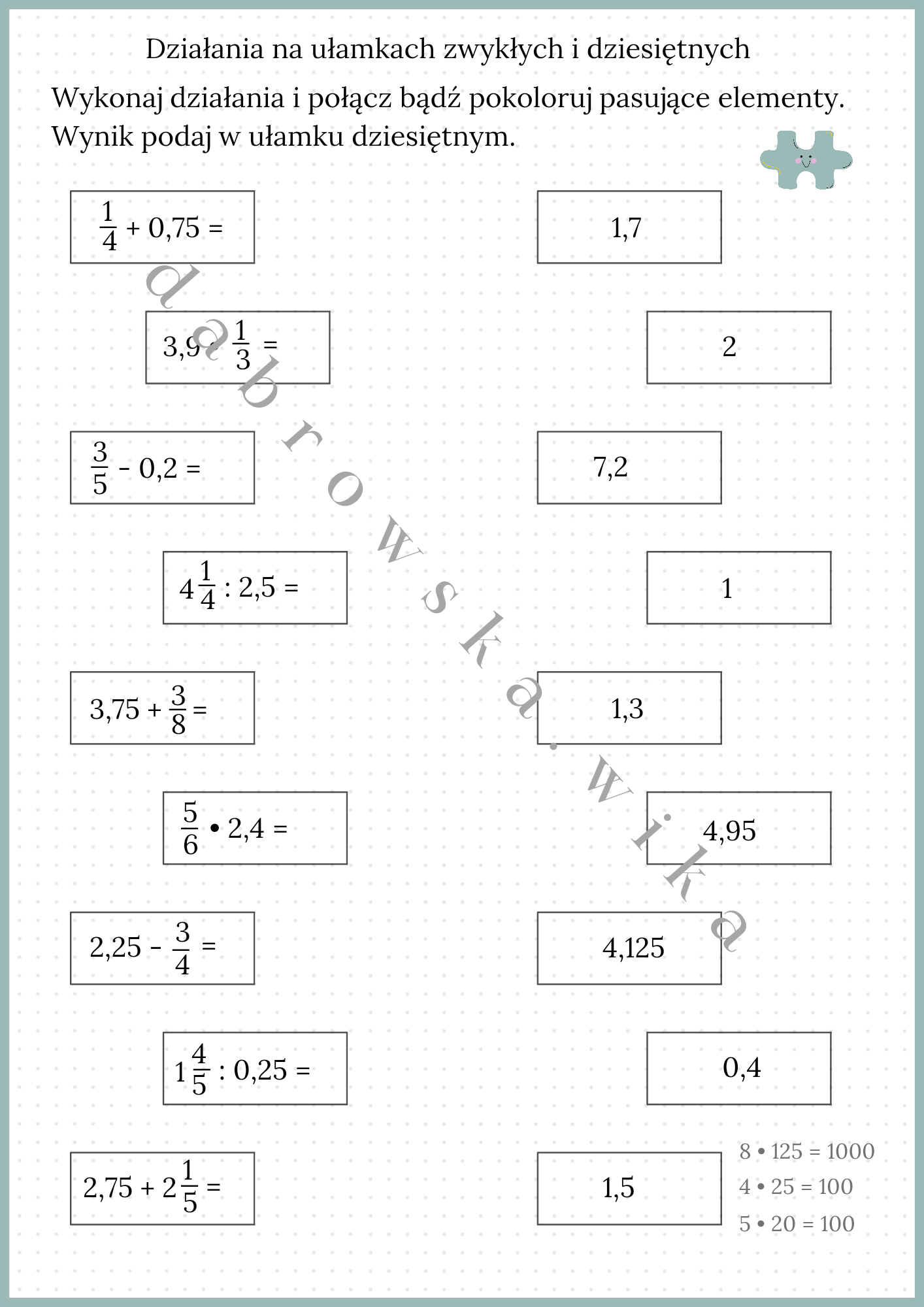
Karta Pracy Działania Na Ułamkach Zwykłych

Karta Pracy Działania Na Ułamkach Zwykłych to zbiór zadań mających na celu ćwiczenie operacji matematycznych na ułamkach zwykłych. Obejmuje dodawanie, odejmowanie, mnożenie i dzielenie ułamków, a także upraszczanie ich do najprostszej postaci.

Aby skutecznie rozwiązywać zadania z karty pracy, należy opanować kilka kluczowych umiejętności. Poniżej przedstawiamy je krok po kroku:

1. Dodawanie i Odejmowanie Ułamków:

Najpierw ułamki muszą mieć wspólny mianownik. Jeśli go nie mają, trzeba go znaleźć (najczęściej jest to najmniejsza wspólna wielokrotność mianowników). Następnie rozszerzamy ułamki, mnożąc licznik i mianownik każdego ułamka przez odpowiednią liczbę, aby uzyskać wspólny mianownik. Potem możemy już dodać lub odjąć liczniki, pozostawiając mianownik bez zmian.

Przykład: 1/3 + 1/4. Wspólny mianownik to 12. 1/3 = 4/12, a 1/4 = 3/12. Zatem 4/12 + 3/12 = 7/12.

2. Mnożenie Ułamków:

Mnożenie ułamków jest prostsze niż dodawanie i odejmowanie! Mnożymy licznik przez licznik i mianownik przez mianownik.

Przykład: 2/5 * 3/7 = (2*3) / (5*7) = 6/35.

3. Dzielenie Ułamków:

Dzielenie ułamków to inaczej mnożenie przez odwrotność drugiego ułamka. Czyli, aby podzielić ułamek przez ułamek, odwracamy drugi ułamek (zamieniamy licznik z mianownikiem) i mnożymy.

Przykład: 1/2 : 2/3 = 1/2 * 3/2 = (1*3) / (2*2) = 3/4.

4. Upraszczanie Ułamków:

Po wykonaniu operacji, warto sprawdzić, czy ułamek można uprościć. Szukamy największego wspólnego dzielnika (NWD) licznika i mianownika i dzielimy przez niego oba.

Przykład: 4/6. NWD(4, 6) = 2. Dzielimy licznik i mianownik przez 2: (4/2) / (6/2) = 2/3.

5. Ułamki Niewłaściwe i Liczby Mieszane:

Ułamek niewłaściwy to ułamek, w którym licznik jest większy lub równy mianownikowi. Można go zamienić na liczbę mieszaną, czyli liczbę całkowitą i ułamek. Dzielimy licznik przez mianownik, wynik dzielenia to część całkowita, reszta to licznik ułamka, a mianownik pozostaje ten sam.

Przykład: 7/3 = 2 i 1/3 (bo 7 dzielone przez 3 daje 2 reszty 1).

Zrozumienie i biegłe operowanie na ułamkach zwykłych jest niezwykle ważne. Praktyczne zastosowanie znajdziemy na przykład w kuchni, gdzie często musimy odmierzać składniki w proporcjach ułamkowych (np. pół szklanki mąki). Innym przykładem jest analiza danych w statystyce lub finansach, gdzie często operujemy na udziałach i procentach, które są formami ułamków.