Jak Zamienić Ułamek Niewłaściwy Na Właściwy

Ułamki stanowią fundamentalną część matematyki i są niezbędne do zrozumienia wielu koncepcji, od codziennych obliczeń po zaawansowane zagadnienia naukowe. Wśród różnych typów ułamków wyróżniamy ułamki właściwe i ułamki niewłaściwe. Rozumienie różnicy między nimi i umiejętność konwertowania ułamka niewłaściwego na właściwy jest kluczową umiejętnością matematyczną.

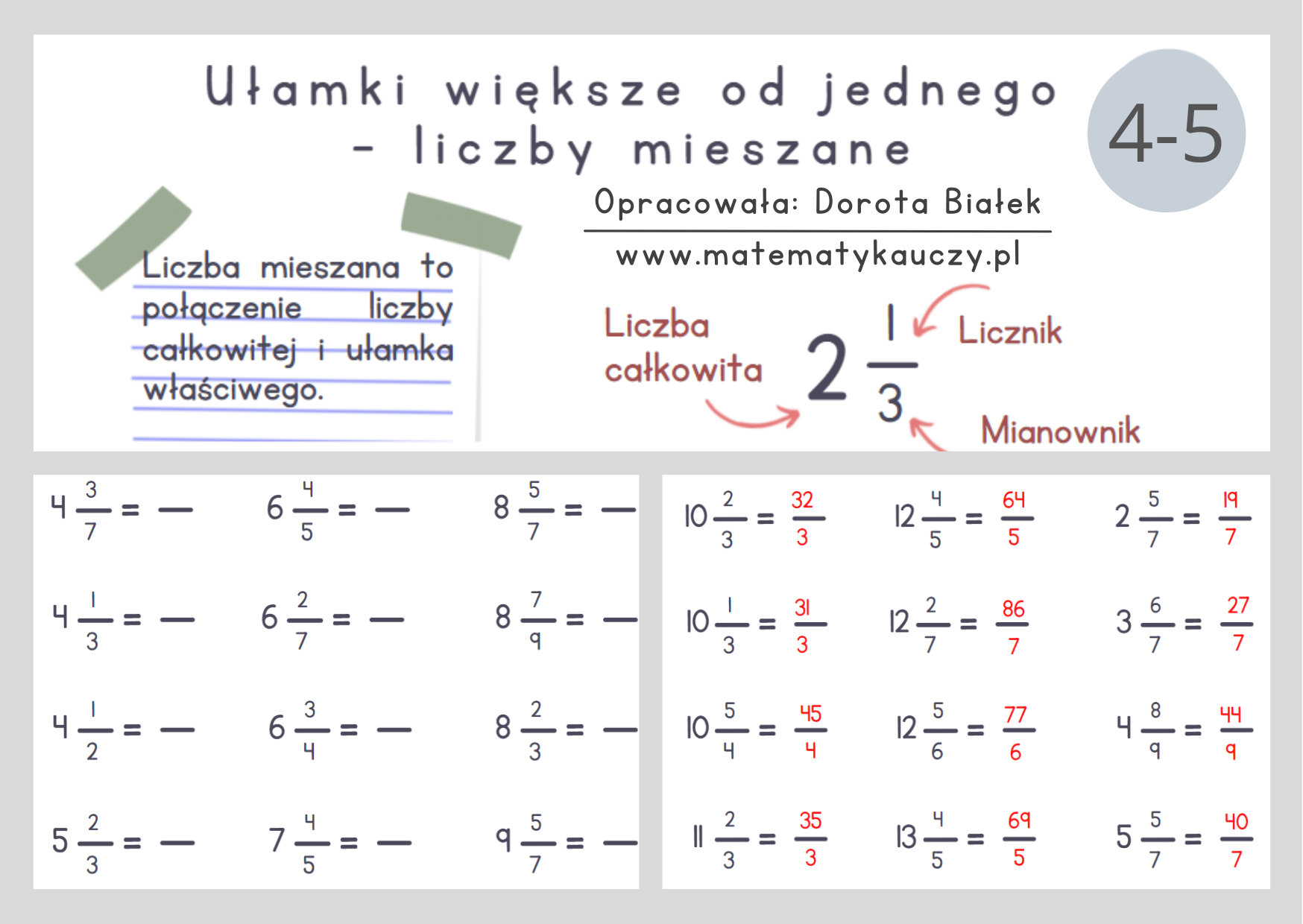
Czym Są Ułamki Właściwe i Niewłaściwe?

Ułamek właściwy to taki ułamek, w którym licznik (górna liczba) jest mniejszy od mianownika (dolna liczba). Przykłady: 1/2, 3/4, 7/10. Ułamek właściwy zawsze reprezentuje wartość mniejszą od 1.

Z kolei ułamek niewłaściwy to ułamek, w którym licznik jest większy lub równy mianownikowi. Przykłady: 5/3, 8/8, 11/4. Ułamek niewłaściwy reprezentuje wartość większą lub równą 1.

Dlaczego Konwertujemy Ułamki Niewłaściwe na Właściwe?

Konwertowanie ułamków niewłaściwych na właściwe (a dokładniej, na liczby mieszane) ma kilka ważnych powodów:

Ułatwienie Zrozumienia Wartości

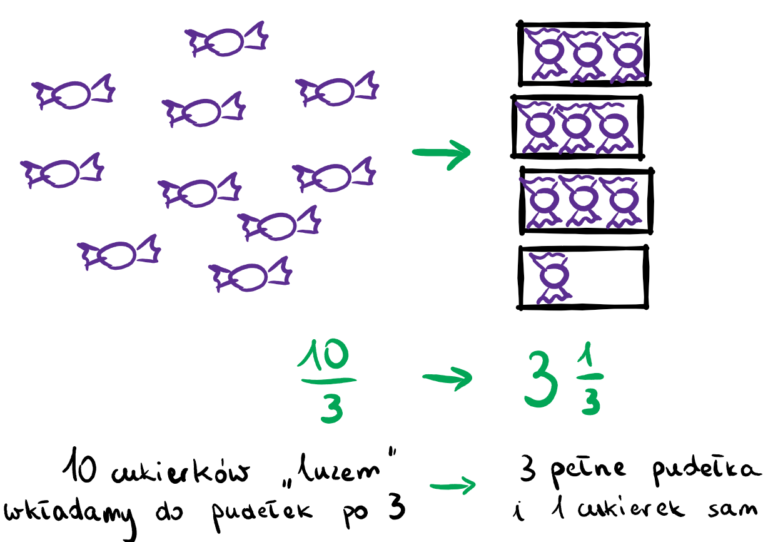
Liczby mieszane (liczba całkowita i ułamek właściwy, np. 1 2/3) są często łatwiejsze do interpretacji niż same ułamki niewłaściwe. Przykładowo, łatwiej wyobrazić sobie 1 2/3 ciasta, niż 5/3 ciasta.

Upraszczanie Wyrażeń

W niektórych obliczeniach i wyrażeniach matematycznych, używanie liczb mieszanych może uprościć dalsze kroki. W szczególności, w działaniach takich jak dodawanie i odejmowanie ułamków.

Wygodniejsza Prezentacja Wyników

W wielu sytuacjach (np. w zadaniach z treścią, w przepisach kulinarnych) wygodniej jest podać wynik w postaci liczby mieszanej, niż w postaci ułamka niewłaściwego.

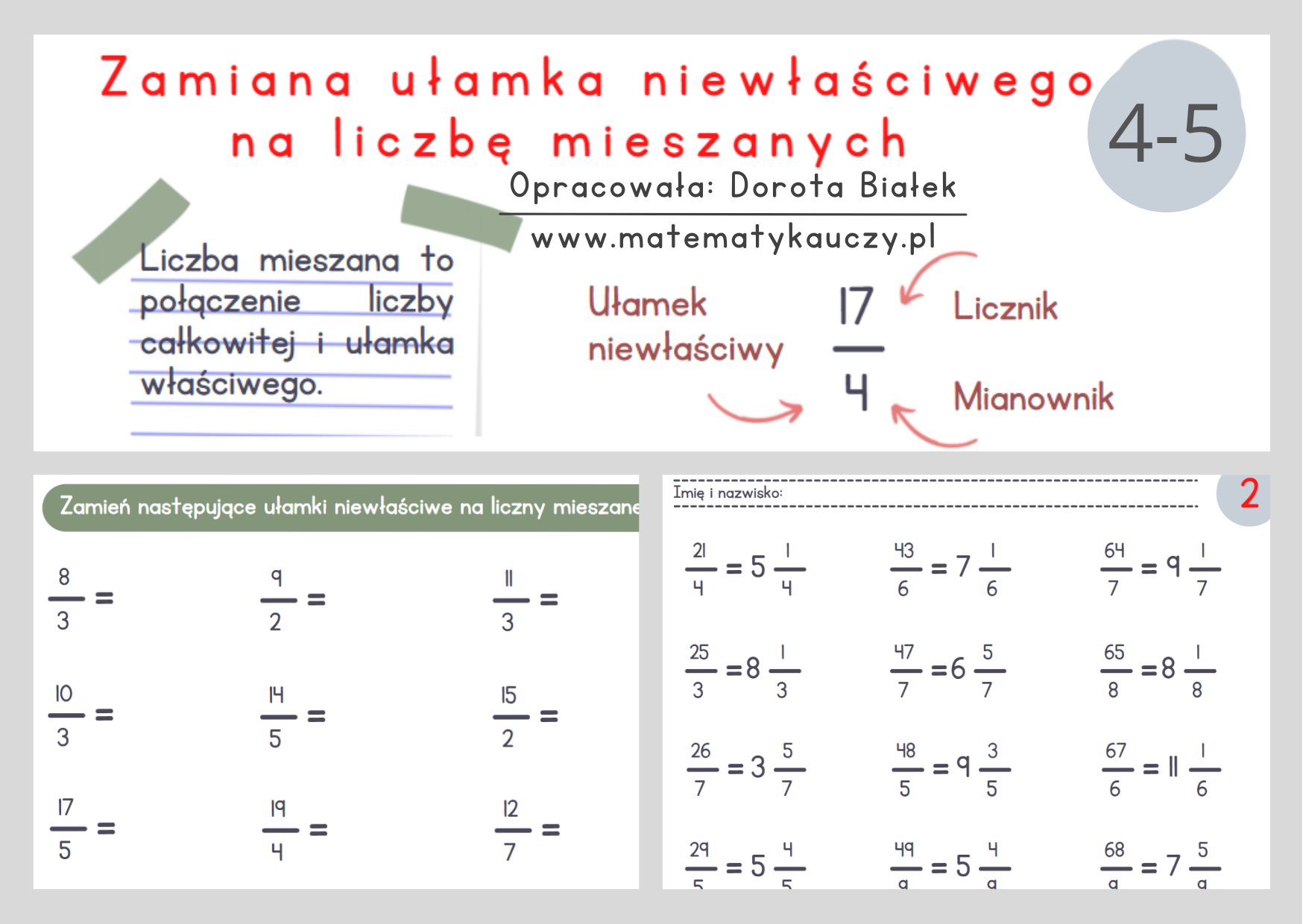
Jak Zamienić Ułamek Niewłaściwy na Liczbę Mieszaną? Krok po Kroku

Proces konwersji ułamka niewłaściwego na liczbę mieszaną jest stosunkowo prosty i opiera się na dzieleniu z resztą:

Krok 1: Podziel Licznik przez Mianownik

Wykonaj dzielenie licznika przez mianownik. Zwróć uwagę na wynik dzielenia (iloraz) oraz resztę z dzielenia.

Przykład: Zamieniamy ułamek 7/3 na liczbę mieszaną. Dzielimy 7 przez 3. 7 ÷ 3 = 2 (iloraz) i reszta 1.

Krok 2: Zapisz Wynik w Postaci Liczby Mieszanej

Iloraz z dzielenia (czyli wynik dzielenia bez reszty) staje się liczbą całkowitą w naszej liczbie mieszanej.

Reszta z dzielenia staje się licznikiem ułamka właściwego.

Mianownik ułamka właściwego pozostaje taki sam jak mianownik ułamka niewłaściwego.

Przykład: Z poprzedniego przykładu, iloraz to 2, a reszta to 1. Zatem liczba mieszana to 2 1/3.

Podsumowanie Kroku po Kroku

1. Podziel licznik przez mianownik.
2. Zapisz iloraz jako liczbę całkowitą.
3. Zapisz resztę jako licznik nowego ułamka.
4. Zachowaj oryginalny mianownik.

Przykłady Zastosowania Konwersji Ułamków

Aby lepiej zrozumieć proces, przeanalizujmy kilka przykładów:

Przykład 1: Zamiana Ułamka 11/4

Dzielimy 11 przez 4: 11 ÷ 4 = 2 (iloraz) i reszta 3.

Liczba mieszana to: 2 3/4.

Przykład 2: Zamiana Ułamka 15/6

Dzielimy 15 przez 6: 15 ÷ 6 = 2 (iloraz) i reszta 3.

Liczba mieszana to: 2 3/6. Zauważmy, że ułamek 3/6 można jeszcze uprościć do 1/2, więc ostatecznie otrzymujemy: 2 1/2.

Przykład 3: Zamiana Ułamka 20/5

Dzielimy 20 przez 5: 20 ÷ 5 = 4 (iloraz) i reszta 0.

W tym przypadku, reszta wynosi 0. Oznacza to, że ułamek 20/5 reprezentuje liczbę całkowitą 4. Formalnie moglibyśmy zapisać to jako 4 0/5, ale najczęściej piszemy po prostu 4.

Praktyczne Zastosowania w Życiu Codziennym

Konwersja ułamków niewłaściwych na liczby mieszane ma wiele zastosowań w życiu codziennym:

Gotowanie

W przepisach kulinarnych często spotykamy się z ułamkami. Wyobraźmy sobie przepis na ciasto, który wymaga 5/4 szklanki mąki. Łatwiej nam odmierzyć 1 1/4 szklanki mąki (jedną pełną szklankę i jedną czwartą), niż operować samym ułamkiem 5/4.

Mierzenie

Podczas mierzenia długości, wagi lub objętości, często uzyskujemy wyniki w postaci ułamków. Przykładowo, długość pewnego przedmiotu może wynosić 11/2 metra. Znów, łatwiej jest nam to zinterpretować jako 1 1/2 metra (jeden i pół metra).

Dzielenie Się

Wyobraźmy sobie, że mamy 7 kawałków pizzy i chcemy podzielić je równo pomiędzy 3 osoby. Każda osoba otrzyma 7/3 pizzy. Zamieniając to na liczbę mieszaną, widzimy, że każda osoba otrzyma 2 1/3 pizzy (dwa całe kawałki i jedną trzecią kawałka).

Błędy, Których Należy Unikać

Podczas konwersji ułamków niewłaściwych na liczby mieszane, warto unikać następujących błędów:

Nieprawidłowe Dzielenie

Najczęstszym błędem jest nieprawidłowe wykonanie dzielenia. Upewnij się, że dokładnie podzieliłeś licznik przez mianownik i poprawnie wyznaczyłeś iloraz oraz resztę.

Zapominanie o Uproszczeniu Ułamka

Po otrzymaniu liczby mieszanej, sprawdź, czy ułamek właściwy można jeszcze uprościć. Jak widzieliśmy w przykładzie 15/6, ułamek 3/6 można uprościć do 1/2.

Pomylenie Licznika z Mianownikiem

Upewnij się, że reszta z dzielenia staje się licznikiem nowego ułamka, a mianownik pozostaje taki sam.

Ułamki w Matematyce Wyższej

Choć konwersja ułamków niewłaściwych na liczby mieszane wydaje się prostą operacją, ma fundamentalne znaczenie w bardziej zaawansowanych dziedzinach matematyki. Zrozumienie relacji między ułamkami właściwymi, niewłaściwymi i liczbami mieszanymi jest kluczowe do pracy z równaniami, funkcjami i innymi koncepcjami matematycznymi.

Ćwiczenia Praktyczne

Aby utrwalić zdobytą wiedzę, spróbuj zamienić następujące ułamki niewłaściwe na liczby mieszane:

• 9/2
• 13/5
• 21/8
• 35/4
• 100/7

Sprawdź swoje odpowiedzi, dzieląc licznik przez mianownik i upewniając się, że poprawnie zinterpretowałeś iloraz i resztę.

Podsumowanie

Konwersja ułamków niewłaściwych na liczby mieszane to ważna umiejętność matematyczna, która ułatwia zrozumienie wartości ułamków, upraszcza obliczenia i umożliwia wygodniejsze prezentowanie wyników. Pamiętaj o krokach dzielenia, poprawnej interpretacji ilorazu i reszty oraz o upraszczaniu ułamków właściwych. Regularne ćwiczenia pozwolą Ci opanować tę umiejętność i pewnie korzystać z niej w różnych sytuacjach.

Zachęcamy do dalszego zgłębiania wiedzy matematycznej i wykorzystywania jej w codziennym życiu!