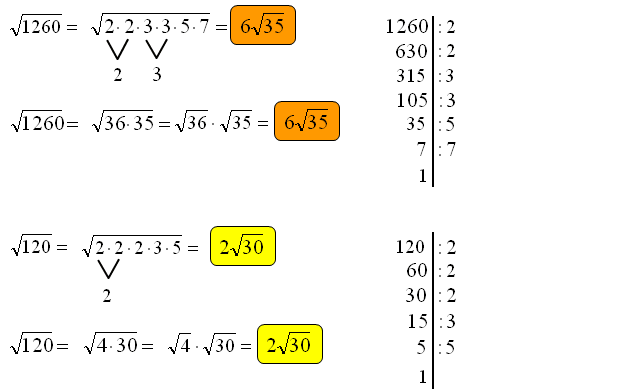Jak Wyłączyć Czynnik Przed Znak Pierwiastka

Masz pierwiastek kwadratowy, np. √8, i słyszysz, że trzeba "wyłączyć czynnik przed znak pierwiastka"? Brzmi skomplikowanie? Spokojnie, to całkiem prosta operacja. Co to jest? To nic innego jak upraszczanie zapisu pierwiastka, tak żeby pod znakiem pierwiastka została jak najmniejsza liczba.
Jak to działa? Zasada jest prosta: szukamy w liczbie pod pierwiastkiem czynników, które są kwadratami liczb całkowitych. Co to znaczy? Przypomnijmy sobie kwadraty liczb: 1 (1*1), 4 (2*2), 9 (3*3), 16 (4*4), 25 (5*5), 36 (6*6) i tak dalej. Jeśli któryś z tych kwadratów "siedzi" w liczbie pod pierwiastkiem, możemy go "wyciągnąć" na zewnątrz.
Weźmy przykład √8. Zastanówmy się, jakie liczby całkowite mnożą się, żeby dać 8. Możemy zapisać 8 jako 4 * 2. O! 4 to kwadrat liczby 2 (2*2=4)! Czyli możemy zapisać:
√8 = √(4 * 2)
A teraz magia: pierwiastek z iloczynu to iloczyn pierwiastków: √(a * b) = √a * √b.
√8 = √(4 * 2) = √4 * √2
√4 wiemy, że to 2, więc:
√8 = 2 * √2 czyli √8 = 2√2
I gotowe! Wyłączyliśmy czynnik 2 przed znak pierwiastka. Zamiast √8 mamy 2√2, co jest prostszym i często bardziej użytecznym zapisem.
Inny przykład: √27. Możemy zapisać 27 jako 9 * 3. 9 to kwadrat liczby 3 (3*3=9)! Czyli:
√27 = √(9 * 3) = √9 * √3 = 3√3
Dlaczego to ma znaczenie?
* Upraszczanie wyrażeń: Często łatwiej jest wykonywać obliczenia z uproszczonymi pierwiastkami. Wyobraź sobie, że masz dodać √8 + √2. Trudne? Ale jeśli zamienimy √8 na 2√2, to mamy 2√2 + √2 = 3√2. Dużo prościej!
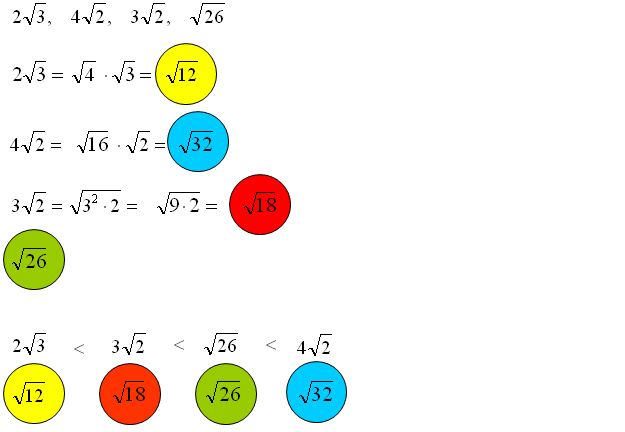
* Porównywanie liczb: Łatwiej jest porównać liczby z uproszczonymi pierwiastkami. Na przykład, które jest większe: √12 czy 3√2? Zamieniamy √12 na √(4 * 3) = √4 * √3 = 2√3. Teraz mamy porównać 2√3 z 3√2. Możemy podnieść obie liczby do kwadratu: (2√3)² = 4 * 3 = 12, a (3√2)² = 9 * 2 = 18. Widzimy, że 3√2 jest większe.
* Dalsza matematyka: Umiejętność wyłączania czynnika przed znak pierwiastka jest niezbędna w wielu działach matematyki, takich jak geometria, trygonometria i analiza matematyczna.
Podsumowując, wyłączanie czynnika przed znak pierwiastka to prosta, ale bardzo przydatna umiejętność, która pozwala upraszczać wyrażenia, porównywać liczby i przygotowuje do bardziej zaawansowanych zagadnień matematycznych. Ćwicz, a szybko opanujesz tę sztukę!