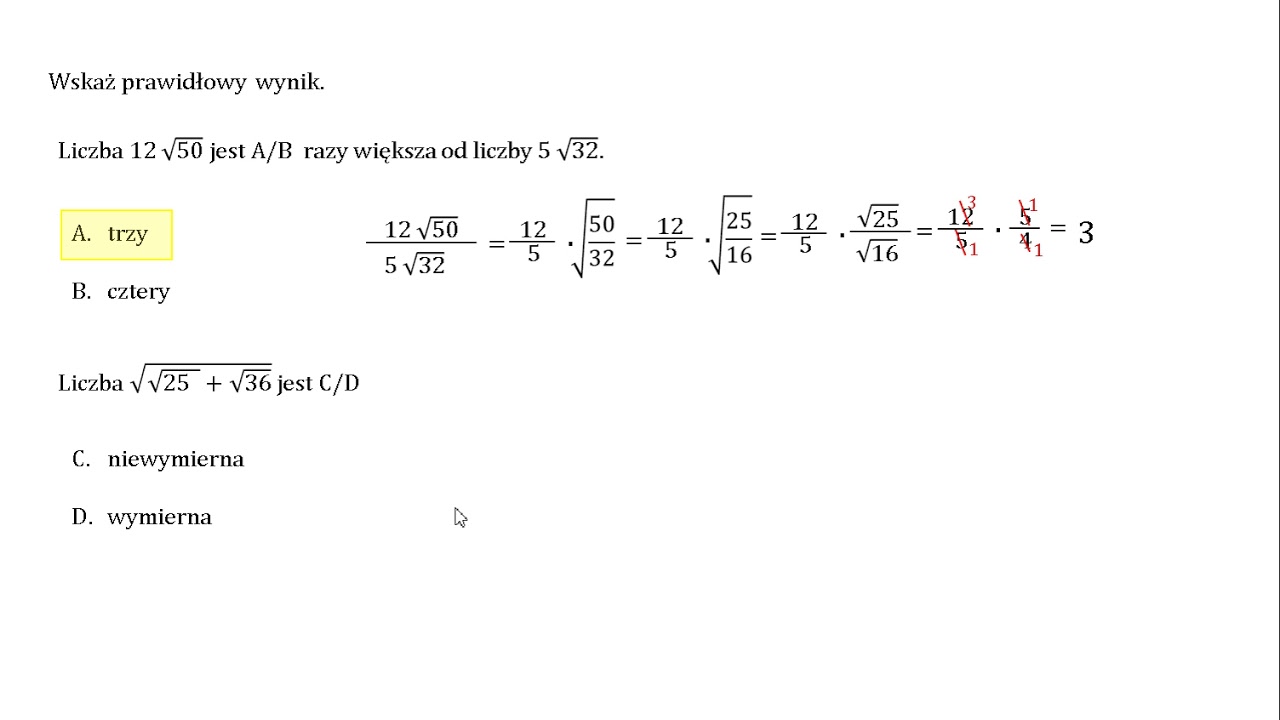Ile Razy Liczba M Jest Większa Od Liczby N

W życiu codziennym często stajemy przed koniecznością porównywania różnych wielkości. Chcemy wiedzieć, co jest większe, mniejsze, a przede wszystkim – ile razy jedna wartość przewyższa drugą. Zagadnienie "Ile razy liczba M jest większa od liczby N" jest fundamentalne w matematyce i ma szerokie zastosowanie w różnych dziedzinach życia, od finansów po naukę i inżynierię. Celem tego artykułu jest dogłębne wyjaśnienie tej koncepcji, zrozumienie jej implikacji i przedstawienie praktycznych przykładów.

Kluczowe Aspekty Porównywania Liczb

Podstawowa Definicja i Obliczenia

Najprościej mówiąc, aby ustalić, ile razy liczba M jest większa od liczby N, wykonujemy dzielenie: M / N. Wynik tego działania mówi nam, ile razy liczba N "mieści się" w liczbie M. Ważne jest, aby pamiętać, że liczba N nie może być zerem, ponieważ dzielenie przez zero jest niedozwolone i prowadzi do nieokreślonych wyników. Jeżeli M jest mniejsze od N, wynik będzie liczbą ułamkową mniejszą od 1. Oznacza to, że M stanowi tylko ułamek liczby N. Na przykład, jeśli M = 10 i N = 2, to 10 / 2 = 5, co oznacza, że M jest 5 razy większe od N.

Różnica między "X razy większe" a "o X większe"

Często mylimy wyrażenia "X razy większe" i "o X większe". Ważne jest, by je rozróżniać, ponieważ prowadzą one do zupełnie innych wyników. "X razy większe" oznacza, że mnożymy liczbę N przez X, aby uzyskać liczbę M (M = N * X). Natomiast "o X większe" oznacza, że dodajemy X do liczby N, aby otrzymać liczbę M (M = N + X). Przykładowo, jeśli liczba N wynosi 5, a M jest "2 razy większa", to M = 5 * 2 = 10. Jeśli M jest "o 2 większa", to M = 5 + 2 = 7. To subtelna, ale istotna różnica.

Zastosowanie Procentów w Porównywaniu

Procenty są użytecznym narzędziem do wyrażania, o ile procent jedna liczba jest większa lub mniejsza od drugiej. Aby obliczyć procentową różnicę, stosujemy następujący wzór: ((M - N) / N) * 100%. Wynik wskazuje, o ile procent liczba M jest większa (lub mniejsza, jeśli wynik jest ujemny) od liczby N. Na przykład, jeśli M = 120 i N = 100, to ((120 - 100) / 100) * 100% = 20%. Oznacza to, że liczba M jest o 20% większa od liczby N.

Przykłady Zastosowań w Rzeczywistości

Finanse i Inwestycje

W finansach koncepcja "ile razy większe" jest kluczowa do oceny zwrotu z inwestycji. Załóżmy, że zainwestowaliśmy 1000 zł, a po roku nasza inwestycja warta jest 1200 zł. Wzrost zysku wynosi 200 zł. Aby dowiedzieć się, ile razy wzrosła nasza inwestycja, możemy obliczyć: 1200/1000 = 1.2. Oznacza to, że nasza inwestycja wzrosła 1.2 razy, albo o 20%. Porównywanie różnych opcji inwestycyjnych pod względem potencjalnych zysków pozwala podejmować bardziej świadome decyzje.

Statystyki i Analiza Danych

W statystyce często porównujemy różne grupy lub zjawiska. Na przykład, możemy porównać średnie wynagrodzenie mężczyzn i kobiet. Załóżmy, że średnie wynagrodzenie mężczyzn wynosi 6000 zł, a kobiet 5000 zł. Aby dowiedzieć się, ile razy wyższe jest wynagrodzenie mężczyzn, obliczamy: 6000 / 5000 = 1.2. Oznacza to, że średnie wynagrodzenie mężczyzn jest 1.2 razy wyższe niż kobiet, albo o 20% wyższe. Takie analizy pomagają identyfikować nierówności i planować działania mające na celu ich eliminację.

Nauka i Inżynieria

W naukach ścisłych i inżynierii porównywanie wielkości jest nieodzowne. Na przykład, możemy porównywać masy różnych obiektów. Jeśli masa jednego obiektu wynosi 10 kg, a drugiego 2 kg, to pierwszy obiekt jest 10/2 = 5 razy cięższy od drugiego. W chemii możemy porównywać stężenia różnych substancji. Jeżeli stężenie roztworu A wynosi 0.5 mol/l, a roztworu B 0.1 mol/l, to stężenie roztworu A jest 0.5/0.1 = 5 razy większe niż stężenie roztworu B.

Handel i Marketing

W handlu i marketingu porównania cen i wielkości produktów są na porządku dziennym. Możemy porównywać ceny produktów różnych marek, aby znaleźć najkorzystniejszą ofertę. Załóżmy, że produkt marki A kosztuje 15 zł, a produkt marki B 10 zł. Produkt marki A jest 15/10 = 1.5 raza droższy niż produkt marki B, albo o 50% droższy. Firmy często wykorzystują takie porównania, aby przekonać klientów do zakupu swoich produktów, podkreślając, że oferują lepszy stosunek jakości do ceny.

Życie Codzienne

Porównywanie liczb przydaje się również w wielu sytuacjach w życiu codziennym. Możemy porównywać zużycie paliwa przez różne samochody. Jeśli samochód A spala 8 litrów paliwa na 100 km, a samochód B spala 6 litrów, to samochód A spala 8/6 = 1.33 razy więcej paliwa niż samochód B. Możemy porównywać powierzchnię mieszkań. Jeśli jedno mieszkanie ma 50 m², a drugie 75 m², to drugie mieszkanie jest 75/50 = 1.5 raza większe od pierwszego. Takie porównania pomagają nam podejmować decyzje dotyczące zakupu, wynajmu lub planowania wydatków.

Praktyczne Dane i Przykłady Statystyczne

Rozważmy przykład porównania PKB (Produkt Krajowy Brutto) różnych krajów. Według danych Banku Światowego, PKB Stanów Zjednoczonych w 2022 roku wynosiło około 25 bilionów dolarów, a PKB Chin około 18 bilionów dolarów. Amerykańskie PKB było zatem 25/18 = 1.39 razy większe niż chińskie. Inny przykład: średnia długość życia w Japonii wynosi około 84 lat, a w Nigerii około 55 lat. Japończycy żyją średnio 84/55 = 1.53 razy dłużej niż Nigeryjczycy. Takie dane, choć uproszczone, ilustrują istotne różnice w rozwoju gospodarczym i społecznym między różnymi krajami.

Spójrzmy na przykład z dziedziny sportu. Załóżmy, że piłkarz A strzelił 30 goli w sezonie, a piłkarz B strzelił 10 goli. Piłkarz A strzelił 30/10 = 3 razy więcej goli niż piłkarz B. Możemy również porównać budżety różnych klubów sportowych. Jeśli budżet klubu X wynosi 100 milionów dolarów, a budżet klubu Y wynosi 25 milionów dolarów, to budżet klubu X jest 100/25 = 4 razy większy od budżetu klubu Y. Te różnice często przekładają się na wyniki sportowe i możliwości inwestycyjne.

Pułapki i Błędy w Porównywaniu Liczb

Podczas porównywania liczb należy unikać pewnych pułapek i błędów. Przede wszystkim, ważne jest, aby upewnić się, że porównywane liczby są wyrażone w tych samych jednostkach. Nie możemy porównywać metrów z centymetrami bez uprzedniego przeliczenia. Kolejnym błędem jest ignorowanie kontekstu. Porównywanie danych bez uwzględnienia czynników zewnętrznych może prowadzić do błędnych wniosków. Na przykład, porównywanie sprzedaży dwóch produktów bez uwzględnienia sezonowości lub działań marketingowych może być mylące. Należy także unikać wyciągania pochopnych wniosków na podstawie małej próby danych. Im większa próba, tym bardziej wiarygodne wyniki.

Podsumowanie i Wnioski

Koncepcja "Ile razy liczba M jest większa od liczby N" jest prostym, ale potężnym narzędziem, które znajduje zastosowanie w wielu dziedzinach życia. Umożliwia nam obiektywne porównywanie różnych wielkości i podejmowanie bardziej świadomych decyzji. Kluczem do poprawnego porównywania jest zrozumienie podstawowych definicji, rozróżnianie między "X razy większe" a "o X większe", oraz unikanie pułapek związanych z jednostkami i kontekstem. Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć tę koncepcję i jej praktyczne zastosowania. Pamiętaj, by zawsze krytycznie analizować dane i zadawać pytania, zanim wyciągniesz ostateczne wnioski.

Działaj! Następnym razem, gdy będziesz musiał/a porównać dwie wielkości, spróbuj zastosować przedstawione tutaj metody. Zauważ, jak to wpływa na twoje zrozumienie problemu. Zadawaj sobie pytania: Czy porównuję wartości w tych samych jednostkach? Czy uwzględniam wszystkie istotne czynniki? Czy wyciągam uzasadnione wnioski? Ćwiczenie czyni mistrza! Im więcej będziesz porównywać i analizować dane, tym lepszy/a się w tym staniesz.