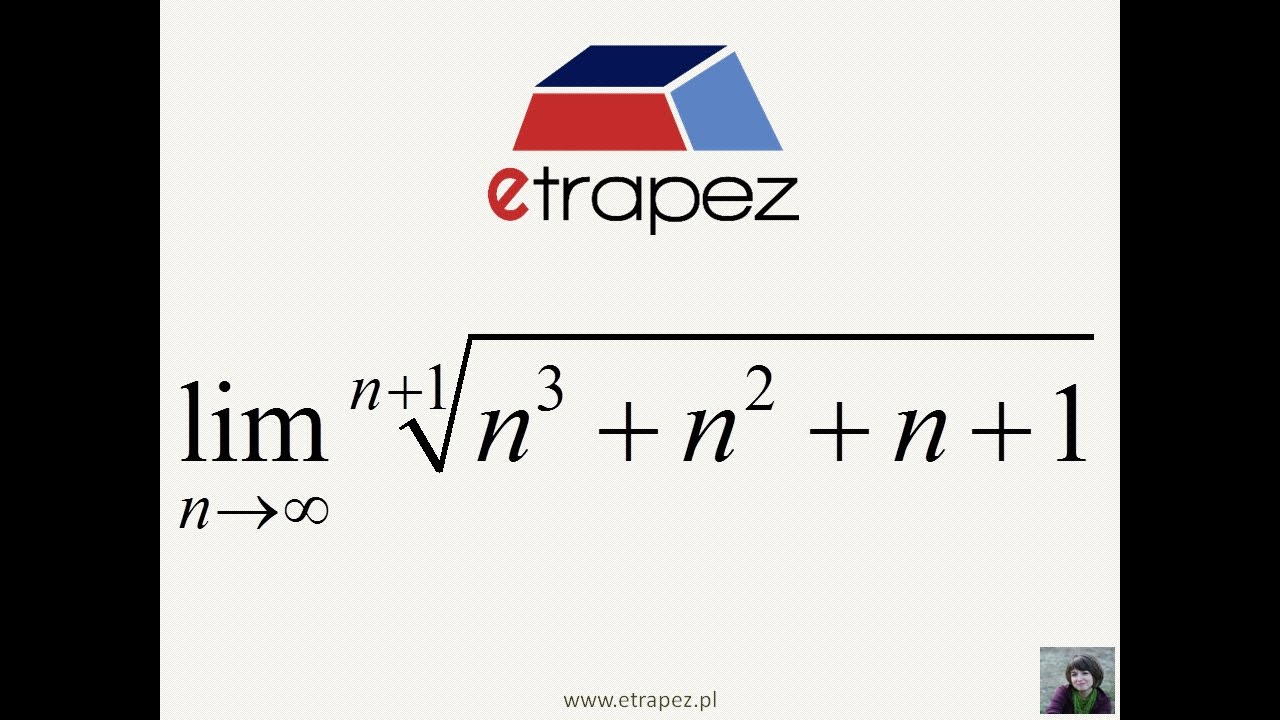Granica Ciągu Twierdzenie O Trzech Ciągach

Zacznijmy od najważniejszego: Co to jest twierdzenie o trzech ciągach? To bardzo przydatne narzędzie w matematyce, które pomaga nam znaleźć granicę trudnego ciągu, porównując go z dwoma innymi, prostszymi ciągami. Mówiąc prościej, wyobraź sobie, że masz trzy ciągi liczb: (a_n), (b_n), i (c_n). Twierdzenie mówi, że jeśli ciąg (b_n) jest "uwięziony" między (a_n) i (c_n), a ciągi (a_n) i (c_n) zbiegają do tej samej granicy, to ciąg (b_n) też musi zbiegać do tej samej granicy.

Jak to działa? Formalnie, twierdzenie mówi, że jeśli:

• a_n ≤ b_n ≤ c_n dla wszystkich n ≥ N (czyli dla wszystkich elementów ciągu od pewnego momentu)
• lim_n→∞ a_n = lim_n→∞ c_n = L (ciągi (a_n) i (c_n) mają tę samą granicę L)

to wtedy: lim_n→∞ b_n = L (ciąg (b_n) też ma granicę L).

Wyobraź sobie to tak: masz kanapkę (b_n). Dwie kromki chleba to (a_n) i (c_n). Jeśli te kromki stają się coraz cieńsze i zbliżają się do siebie, aż w końcu prawie znikają (mają granicę 0), to i kanapka (b_n) musi stać się coraz cieńsza i też zmierzać do zera. Ważne, żeby kanapka (b_n) zawsze była pomiędzy kromkami (a_n) i (c_n).

Dlaczego to ma znaczenie? Często mamy do czynienia z ciągami, których granicę ciężko obliczyć bezpośrednio. Twierdzenie o trzech ciągach pozwala nam "obejść" ten problem. Znajdujemy dwa prostsze ciągi, które "otaczają" nasz trudny ciąg i których granice łatwo obliczyć. Jeśli te granice są takie same, to znamy już granicę naszego trudnego ciągu!

Przykład: Rozważmy ciąg b_n = (sin n) / n. Bezpośrednie policzenie granicy tego ciągu może być trudne. Ale wiemy, że -1 ≤ sin n ≤ 1. Dzieląc wszystkie strony tej nierówności przez n, otrzymujemy:

-1/n ≤ (sin n) / n ≤ 1/n

Teraz mamy dwa ciągi: a_n = -1/n i c_n = 1/n. Oba te ciągi zbiegają do 0 (lim_n→∞ -1/n = 0 i lim_n→∞ 1/n = 0). Zatem, z twierdzenia o trzech ciągach, lim_n→∞ (sin n) / n = 0.

Podsumowując, twierdzenie o trzech ciągach jest potężnym narzędziem, które pozwala obliczyć granice trudnych ciągów, porównując je z dwoma prostszymi. Pamiętaj o "uwięzieniu" ciągu i wspólnej granicy otaczających ciągów, a na pewno dasz radę!