Graniastosłupy I Ostrosłupy Zadania Klasa 8

Witajcie, drodzy uczniowie klasy 8! Rozumiem, że graniastosłupy i ostrosłupy mogą wydawać się na początku zagadkowe i trudne. Pewnie wielu z Was zastanawia się, po co w ogóle uczyć się o tych dziwnych figurach. Przecież na co dzień nie chodzimy po ulicy mierząc objętości dachów, prawda? Otóż nie do końca! Geometria przestrzenna otacza nas ze wszystkich stron, a zrozumienie jej zasad pozwala lepiej orientować się w świecie i rozwiązywać problemy, które pozornie wydają się nie mieć z nią nic wspólnego.

Zanim przejdziemy do konkretnych zadań, spróbujmy wyobrazić sobie codzienne sytuacje, w których wiedza o graniastosłupach i ostrosłupach może się przydać:

Projektowanie pokoju: Chcesz pomalować pokój i zastanawiasz się, ile farby potrzebujesz? Musisz obliczyć powierzchnię ścian, które często mają kształt prostokątów (a prostokąt to podstawa graniastosłupa!).
Gotowanie: Przepis mówi o formie do pieczenia o określonej objętości. Musisz wybrać odpowiednią, by ciasto się zmieściło.
Budownictwo: Architekci i budowniczowie na co dzień korzystają z wiedzy o graniastosłupach i ostrosłupach, projektując budynki, dachy i inne konstrukcje.
Pakowanie prezentów: Chcesz zapakować prezent w nietypowe pudełko? Zrozumienie geometrii pomoże Ci wybrać odpowiedni rozmiar i kształt.

Widzicie? Geometria jest wszędzie! A teraz przejdźmy do konkretnych przykładów i zadań, które pomogą Wam opanować graniastosłupy i ostrosłupy.

Graniastosłupy - Przyjazny wprowadzenie

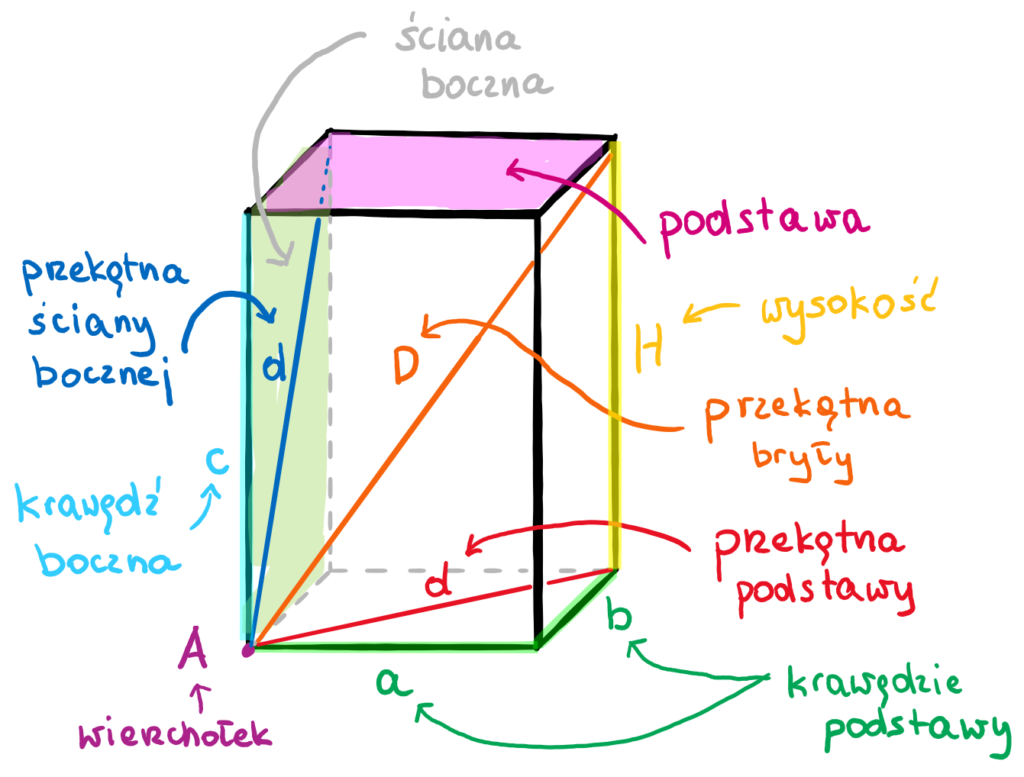
Graniastosłup to bryła, która ma dwie identyczne podstawy (w kształcie dowolnego wielokąta) połączone ścianami bocznymi, które są równoległobokami (najczęściej prostokątami). Wyobraźcie sobie pudełko czekoladek, namiot turystyczny, czy budynek – wiele z nich przypomina graniastosłupy. Istotne jest to, że obie podstawy są identyczne i równoległe do siebie.

Rodzaje graniastosłupów:

Graniastosłup prosty: Ściany boczne są prostokątami i są prostopadłe do podstawy. To najczęściej spotykany rodzaj graniastosłupa.
Graniastosłup prawidłowy: To graniastosłup prosty, którego podstawa jest wielokątem foremnym (np. trójkątem równobocznym, kwadratem, pięciokątem foremnym).
Graniastosłup pochyły: Ściany boczne nie są prostopadłe do podstawy.

Ważne wzory:

Pole powierzchni całkowitej (Pc): Pc = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Objętość (V): V = Pp * H, gdzie Pp to pole podstawy, a H to wysokość graniastosłupa.

Zadanie 1:

Oblicz pole powierzchni całkowitej i objętość graniastosłupa prawidłowego czworokątnego o krawędzi podstawy 5 cm i wysokości 10 cm.

Rozwiązanie:

Podstawa to kwadrat o boku 5 cm, więc Pp = 5 cm * 5 cm = 25 cm².
Powierzchnia boczna składa się z czterech prostokątów o wymiarach 5 cm x 10 cm. Zatem Pb = 4 * (5 cm * 10 cm) = 200 cm².
Pole powierzchni całkowitej: Pc = 2 * 25 cm² + 200 cm² = 250 cm².
Objętość: V = 25 cm² * 10 cm = 250 cm³.

Zadanie 2:

Podstawą graniastosłupa prostego jest trójkąt prostokątny o przyprostokątnych 3 cm i 4 cm. Wysokość graniastosłupa wynosi 8 cm. Oblicz objętość graniastosłupa.

Rozwiązanie:

Pole trójkąta prostokątnego (podstawy): Pp = (1/2) * 3 cm * 4 cm = 6 cm².
Objętość: V = 6 cm² * 8 cm = 48 cm³.

Ostrosłupy - Szpiczasty świat

Ostrosłup to bryła, która ma jedną podstawę (w kształcie dowolnego wielokąta) i jeden wierzchołek, który nie leży na płaszczyźnie podstawy. Ściany boczne są trójkątami, które schodzą się w tym wierzchołku. Piramida w Egipcie to doskonały przykład ostrosłupa.

Rodzaje ostrosłupów:

Ostrosłup prosty: Spodek wysokości (punkt, w którym wysokość opuszczona z wierzchołka pada na podstawę) leży w środku okręgu opisanego na podstawie.
Ostrosłup prawidłowy: To ostrosłup prosty, którego podstawa jest wielokątem foremnym.
Ostrosłup pochyły: Spodek wysokości nie leży w środku okręgu opisanego na podstawie.

Ważne wzory:

Pole powierzchni całkowitej (Pc): Pc = Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Objętość (V): V = (1/3) * Pp * H, gdzie Pp to pole podstawy, a H to wysokość ostrosłupa.

Zadanie 3:

Oblicz pole powierzchni całkowitej i objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 6 cm i wysokości 4 cm.

Rozwiązanie:

Podstawa to kwadrat o boku 6 cm, więc Pp = 6 cm * 6 cm = 36 cm².
Musimy obliczyć wysokość ściany bocznej (h). Tworzy ona trójkąt prostokątny z połową boku podstawy (3 cm) i wysokością ostrosłupa (4 cm). Z twierdzenia Pitagorasa: h² = 3² + 4² = 9 + 16 = 25. Zatem h = 5 cm.
Pole jednej ściany bocznej: (1/2) * 6 cm * 5 cm = 15 cm². Powierzchnia boczna składa się z czterech takich ścian, więc Pb = 4 * 15 cm² = 60 cm².
Pole powierzchni całkowitej: Pc = 36 cm² + 60 cm² = 96 cm².
Objętość: V = (1/3) * 36 cm² * 4 cm = 48 cm³.

Zadanie 4:

Podstawą ostrosłupa jest prostokąt o bokach 8 cm i 6 cm. Wysokość ostrosłupa wynosi 10 cm. Oblicz objętość ostrosłupa.

Rozwiązanie:

Pole prostokąta (podstawy): Pp = 8 cm * 6 cm = 48 cm².
Objętość: V = (1/3) * 48 cm² * 10 cm = 160 cm³.

Pułapki i trudności - Jak ich unikać?

Podczas rozwiązywania zadań z graniastosłupów i ostrosłupów, można napotkać pewne typowe trudności. Oto kilka z nich i sposoby na ich pokonanie:

Pomylenie wzorów: Pamiętaj o różnicy we wzorach na objętość graniastosłupa (V = Pp * H) i ostrosłupa (V = (1/3) * Pp * H). Ten współczynnik 1/3 jest kluczowy dla ostrosłupów!
Brak wyobraźni przestrzennej: Ważne jest, by umieć wyobrazić sobie bryłę w przestrzeni. Spróbuj rysować pomocnicze rysunki lub korzystać z modeli (np. z papieru).
Trudności z obliczeniem pola podstawy: Przypomnij sobie wzory na pola różnych figur (kwadrat, prostokąt, trójkąt, trapez, itd.). Jeśli podstawa jest bardziej skomplikowana, spróbuj ją podzielić na mniejsze, prostsze figury.
Problem z twierdzeniem Pitagorasa: Często musisz obliczyć długość krawędzi, wysokość ściany bocznej, czy wysokość ostrosłupa, korzystając z twierdzenia Pitagorasa. Upewnij się, że prawidłowo identyfikujesz boki trójkąta prostokątnego (przeciwprostokątna i przyprostokątne).
Brak jednostek: Zawsze pamiętaj o podawaniu jednostek w wynikach (cm, cm², cm³, itd.).

Counterpoints – Co, jeśli nie lubię geometrii?

Rozumiem, że nie każdy musi kochać geometrię. Niektórzy wolą historię, inni literaturę. Ale nawet jeśli geometria nie jest Twoim ulubionym przedmiotem, warto zrozumieć jej podstawy. Dlaczego? Bo rozwija logiczne myślenie, umiejętność rozwiązywania problemów i wyobraźnię przestrzenną – a te umiejętności przydadzą Ci się w wielu dziedzinach życia, niezależnie od tego, czym będziesz się zajmować.

Inni mogą uważać, że geometria to tylko teoria, która nie ma zastosowania w praktyce. Ale, jak pokazałem na początku, geometria otacza nas ze wszystkich stron. Dzięki niej możemy projektować budynki, obliczać zużycie materiałów, czy nawet lepiej zrozumieć otaczający nas świat.

Podsumowanie i co dalej?

Mam nadzieję, że ten artykuł pomógł Wam lepiej zrozumieć graniastosłupy i ostrosłupy. Pamiętajcie, że kluczem do sukcesu jest praktyka. Rozwiązujcie jak najwięcej zadań, korzystajcie z podręczników, zeszytów ćwiczeń i internetowych zasobów. Nie bójcie się pytać nauczyciela o pomoc, jeśli czegoś nie rozumiecie. Pamiętajcie, że nauka to proces, a każdy ma prawo do pomyłek.

Teraz, gdy już znasz podstawy, możesz spróbować zmierzyć się z bardziej skomplikowanymi zadaniami, np. takimi, które wymagają zastosowania kilku wzorów naraz, albo takich, w których trzeba obliczyć brakujące dane, korzystając z podanych informacji. Możesz też spróbować poszukać w swoim otoczeniu przykładów graniastosłupów i ostrosłupów i spróbować oszacować ich objętość.

Czy zastanawiałeś/aś się kiedyś, jak wiedza o graniastosłupach i ostrosłupach może pomóc Ci w Twoich zainteresowaniach, np. w modelarstwie, grach komputerowych, czy architekturze? Spróbuj znaleźć powiązania! To może sprawić, że geometria stanie się dla Ciebie bardziej interesująca i przydatna.