Graniastosłup Prosty Ma Wysokość Równą 5 Cm

Geometria, królowa nauk, nieustannie zaskakuje nas swoją precyzją i elegancją. Wśród wielu fascynujących figur, prym wiodą bryły, a szczególnym zainteresowaniem cieszą się graniastosłupy. Dziś skupimy się na konkretnym typie – graniastosłupie prostym – i to takim, którego wysokość wynosi dokładnie 5 cm. Co to dla nas oznacza? Jakie właściwości i zastosowania ma taka figura? Spróbujmy to wspólnie zgłębić.

Czym jest Graniastosłup Prosty?

Zanim przejdziemy do szczegółów, warto przypomnieć sobie definicję. Graniastosłup to bryła, której podstawy są przystającymi wielokątami leżącymi w równoległych płaszczyznach, a ściany boczne są równoległobokami. Graniastosłup prosty charakteryzuje się tym, że jego ściany boczne są prostokątami, a krawędzie boczne są prostopadłe do podstaw. To oznacza, że wysokość graniastosłupa prostego jest równa długości jego krawędzi bocznej. W naszym przypadku ta długość wynosi 5 cm.

Podstawowe Elementy i Właściwości Graniastosłupa Prostego

Aby lepiej zrozumieć omawiany obiekt, przyjrzyjmy się jego podstawowym elementom:

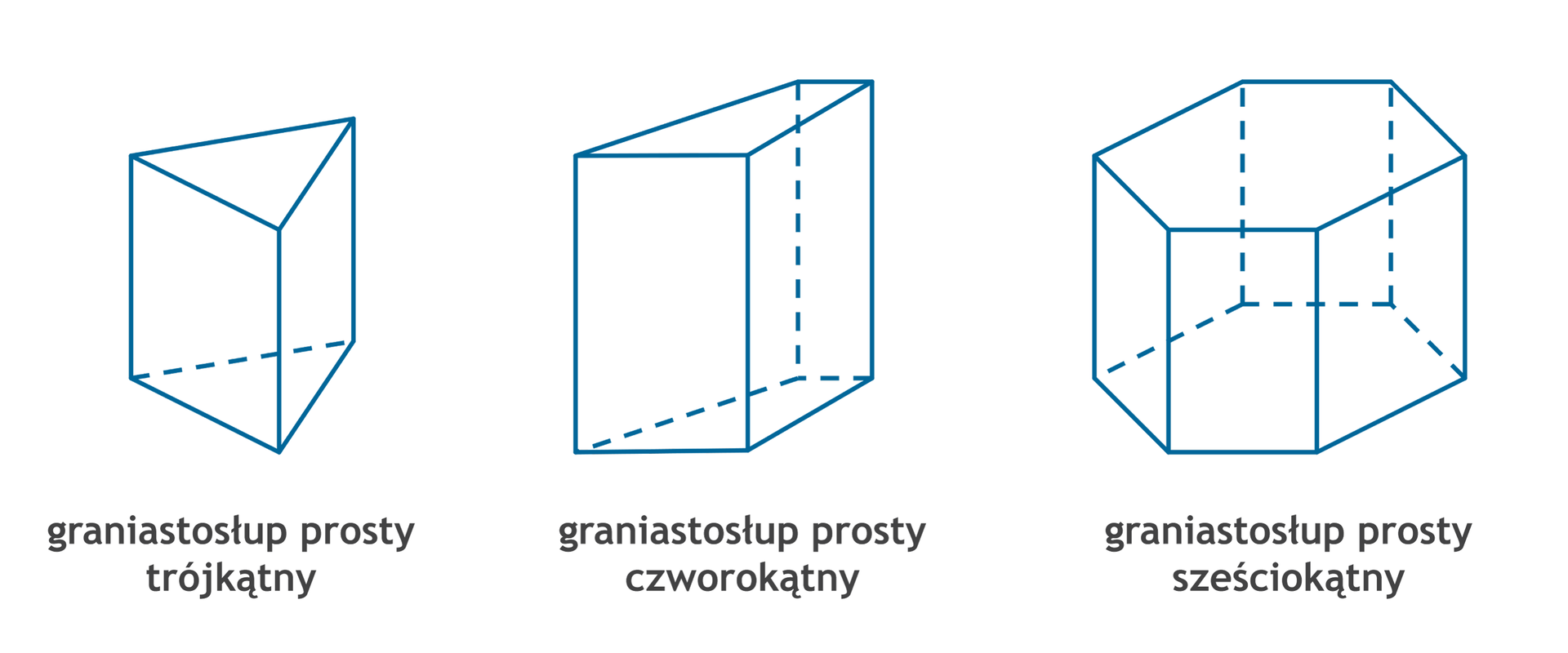
Podstawy: Dwa przystające wielokąty, leżące w równoległych płaszczyznach. Mogą to być trójkąty, czworokąty, pięciokąty itd. Kształt podstawy definiuje typ graniastosłupa (np. graniastosłup trójkątny, czworokątny, pięciokątny).
Ściany boczne: Prostokąty łączące odpowiadające sobie boki podstaw. Ich liczba jest równa liczbie boków w podstawie.
Krawędzie: Odcinki, w których stykają się ściany graniastosłupa. Wyróżniamy krawędzie podstawy (znajdujące się w podstawach) i krawędzie boczne (łączące podstawy).
Wierzchołki: Punkty, w których zbiegają się krawędzie.
Wysokość (H): Odległość między podstawami, w przypadku graniastosłupa prostego równa długości krawędzi bocznej. W naszym przypadku H = 5 cm.

Graniastosłup Prosty o Wysokości 5 cm - Co to Oznacza?

Skupmy się teraz na tym, co oznacza fakt, że nasz graniastosłup ma wysokość 5 cm. Przede wszystkim, ustala to jedną z podstawowych cech geometrycznych bryły. Oznacza to, że niezależnie od kształtu podstawy, odległość między płaszczyznami, w których leżą podstawy, wynosi 5 cm. To istotne przy obliczaniu pola powierzchni i objętości graniastosłupa.

Wpływ Wysokości na Pole Powierzchni

Pole powierzchni graniastosłupa prostego składa się z sumy pól dwóch podstaw i pól wszystkich ścian bocznych. Pole powierzchni całkowitej (Pc) możemy obliczyć ze wzoru: Pc = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej. Pole powierzchni bocznej jest sumą pól wszystkich prostokątnych ścian bocznych. Ponieważ ściany boczne są prostokątami, ich pole to długość boku podstawy pomnożona przez wysokość graniastosłupa (5 cm). A więc, im większy obwód podstawy, tym większe pole powierzchni bocznej.

Przykład: Rozważmy graniastosłup prosty trójkątny o wysokości 5 cm. Podstawa jest trójkątem równobocznym o boku a = 3 cm. Wtedy obwód podstawy wynosi 9 cm, a pole powierzchni bocznej to 9 cm * 5 cm = 45 cm². Pole podstawy (trójkąta równobocznego) wynosi (a² * √3) / 4 = (9 * √3) / 4 ≈ 3.9 cm². Pole powierzchni całkowitej graniastosłupa wynosi zatem 2 * 3.9 cm² + 45 cm² ≈ 52.8 cm².

Wpływ Wysokości na Objętość

Objętość graniastosłupa prostego jest stosunkowo prosta do obliczenia. Wyraża się wzorem: V = Pp * H, gdzie Pp to pole podstawy, a H to wysokość graniastosłupa. W naszym przypadku, V = Pp * 5 cm. Zauważ, że objętość graniastosłupa zależy wprost proporcjonalnie od pola podstawy – im większe pole podstawy, tym większa objętość graniastosłupa o tej samej wysokości.

Przykład: Weźmy ten sam graniastosłup prosty trójkątny o wysokości 5 cm z trójkątem równobocznym o boku 3 cm jako podstawą. Jak już wyliczyliśmy, pole podstawy wynosi około 3.9 cm². Wobec tego objętość tego graniastosłupa to V = 3.9 cm² * 5 cm = 19.5 cm³.

Realne Zastosowania Graniastosłupów Prostych

Choć graniastosłupy proste wydają się być abstrakcyjnymi obiektami matematycznymi, mają one szerokie zastosowanie w życiu codziennym i różnych dziedzinach nauki i techniki:

Architektura i budownictwo: Wiele budynków, szczególnie tych o prostych, geometrycznych kształtach, można przybliżyć do graniastosłupów. Słupy, belki, a nawet całe fragmenty budynków mogą mieć kształt graniastosłupa.
Inżynieria: Elementy konstrukcyjne mostów, tuneli, maszyn często mają kształt graniastosłupów. Znajomość ich właściwości geometrycznych jest kluczowa dla zapewnienia stabilności i wytrzymałości konstrukcji.
Projektowanie: Wzornictwo przemysłowe, projektowanie mebli, opakowań – wszędzie tam spotykamy się z formami zbliżonymi do graniastosłupów.
Matematyka i fizyka: Graniastosłupy proste są często wykorzystywane jako modele do nauki geometrii przestrzennej, obliczania pól powierzchni i objętości, a także do analizy statycznej w fizyce.
Krystalografia: Wiele kryształów posiada strukturę zbliżoną do graniastosłupów prostych. Zrozumienie ich geometrii pozwala na lepsze poznanie właściwości materiałów.
Opakowania: Wiele pudełek i pojemników ma kształt graniastosłupa prostego, co ułatwia ich produkcję, transport i składowanie.

Przykłady z Życia Wzięte:

Cegła: Przybliżony graniastosłup prosty. Jej wymiary mają kluczowe znaczenie dla stabilności ścian i murów.
Pudełko na buty: Typowy graniastosłup prosty o podstawie prostokąta.
Słupy podtrzymujące dach w stodole: Często mają kształt graniastosłupów prostych.
Kryształ kwarcu: Niektóre kryształy kwarcu wykazują strukturę graniastosłupa.

Znaczenie dla Rozwiązywania Zadań Matematycznych

Zadania z graniastosłupami prostymi o znanej wysokości, np. 5 cm, często pojawiają się na lekcjach matematyki i na egzaminach. Umiejętność obliczania pola powierzchni i objętości takich brył jest kluczowa dla zdania egzaminów i rozwijania umiejętności logicznego myślenia. W zadaniach często podaje się informacje o podstawie graniastosłupa (np. długości boków, kąty) i wymaga obliczenia pola powierzchni lub objętości. Zadania te uczą łączenia wiedzy z zakresu geometrii płaskiej (własności wielokątów) z geometrią przestrzenną.

Podsumowanie

Graniastosłup prosty o wysokości 5 cm to konkretny, ale wszechstronny obiekt geometryczny. Jego właściwości geometryczne, takie jak pole powierzchni i objętość, zależą od kształtu i wymiarów podstawy, ale wysokość 5 cm ustala ważny parametr, który wpływa na te obliczenia. Zrozumienie właściwości graniastosłupów prostych jest ważne zarówno w kontekście matematycznym, jak i w zastosowaniach praktycznych w różnych dziedzinach. Pamiętajmy, że geometria to nie tylko suche wzory, ale także klucz do zrozumienia otaczającego nas świata.

Zachęcam do dalszego zgłębiania wiedzy na temat brył geometrycznych i ich zastosowań. Ćwiczcie obliczanie pola powierzchni i objętości różnych graniastosłupów, a zobaczycie, jak geometria staje się coraz bardziej fascynująca i przydatna.