Funkcja Kwadratowa F Jest Określona Wzorem

Funkcja kwadratowa jest funkcją, która może być zdefiniowana wzorem f(x) = ax² + bx + c, gdzie a, b, c są liczbami rzeczywistymi oraz a ≠ 0. Jest to fundamentalny typ funkcji w matematyce, szeroko stosowany w modelowaniu różnych zjawisk.

Rozważmy krok po kroku, jak analizować i rozumieć funkcję kwadratową:

Identyfikacja współczynników: Pierwszym krokiem jest rozpoznanie współczynników a, b i c w danej funkcji. Na przykład, w funkcji f(x) = 2x² - 3x + 1, mamy a = 2, b = -3, c = 1.
Określenie kierunku ramion paraboli: Znak współczynnika a determinuje, czy parabola (wykres funkcji kwadratowej) ma ramiona skierowane do góry (a > 0) czy do dołu (a < 0). W przykładzie powyżej, a = 2 > 0, więc ramiona paraboli są skierowane do góry. Jeśli mielibyśmy f(x) = -x² + 5x - 4, to a = -1 < 0, a ramiona byłyby skierowane do dołu.
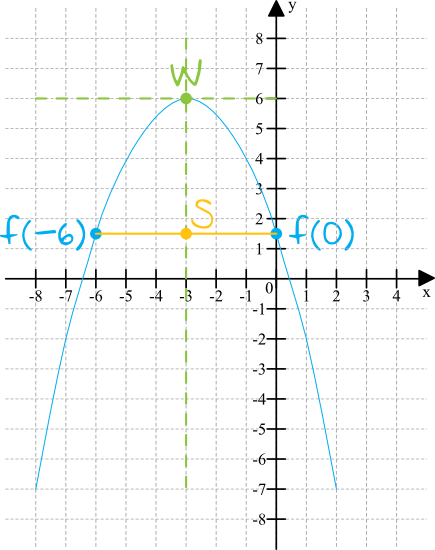
Obliczenie wierzchołka paraboli: Wierzchołek paraboli to punkt, w którym funkcja osiąga minimum (jeśli a > 0) lub maksimum (jeśli a < 0). Współrzędne wierzchołka (p, q) obliczamy ze wzorów: p = -b / (2a) oraz q = f(p). Dla f(x) = 2x² - 3x + 1, mamy p = -(-3) / (2 * 2) = 3/4, a q = f(3/4) = 2*(3/4)² - 3*(3/4) + 1 = -1/8. Zatem wierzchołek to (3/4, -1/8).
Znalezienie miejsc zerowych: Miejsca zerowe funkcji to wartości x, dla których f(x) = 0. Obliczamy je, rozwiązując równanie kwadratowe ax² + bx + c = 0. Używamy do tego delty (Δ = b² - 4ac). Jeśli Δ > 0, funkcja ma dwa miejsca zerowe; jeśli Δ = 0, ma jedno miejsce zerowe (wierzchołek paraboli leży na osi OX); a jeśli Δ < 0, funkcja nie ma miejsc zerowych. Dla f(x) = 2x² - 3x + 1, Δ = (-3)² - 4 * 2 * 1 = 1. Miejsca zerowe to x₁ = (3 - 1) / 4 = 1/2 oraz x₂ = (3 + 1) / 4 = 1.
Wyznaczenie punktu przecięcia z osią OY: Punkt przecięcia z osią OY znajduje się w punkcie (0, c). Dla f(x) = 2x² - 3x + 1, funkcja przecina oś OY w punkcie (0, 1).

Praktyczne zastosowania: Funkcja kwadratowa znajduje zastosowanie w wielu dziedzinach. Przykładowo, w fizyce, można jej użyć do modelowania toru lotu rzuconego przedmiotu (zaniedbując opór powietrza). W ekonomii, może reprezentować zależność pomiędzy ceną a popytem na dany produkt, pomagając w optymalizacji strategii cenowych.

Znajomość własności funkcji kwadratowej jest kluczowa w dalszej nauce matematyki i w wielu jej zastosowaniach w świecie rzeczywistym.