Figury Obrotowe I Wielościany Sprawdzian Gimnazjum

Wiem, że perspektywa sprawdzianu z matematyki może budzić niepokój, zwłaszcza gdy na tapecie pojawiają się zagadnienia takie jak figury obrotowe i wielościany. To tematy, które dla wielu uczniów gimnazjum bywają nieco abstrakcyjne i trudne do wyobrażenia. Ale spokojnie! Nie jesteś sam/a w tych odczuciach. Zrozumienie tych brył to klucz do sukcesu, a ja jestem tu, aby Ci w tym pomóc.

Pomyśl przez chwilę: jak często w codziennym życiu spotykasz się z bryłami? Od puszki po napoje, przez piłkę, po dach budynku – wszędzie są wokół nas! Właśnie te podstawowe kształty, które otaczają nas w rzeczywistości, stanowią fundament, na którym opiera się sprawdzian. Celem tego artykułu jest nie tylko przygotowanie Cię do testu, ale także pokazanie, że matematyka może być fascynująca i bliska Twojemu światu.

Klucz do Zrozumienia: Wizualizacja i Praktyka

Największym wyzwaniem przy nauce figur obrotowych i wielościanów jest często wyobrażenie sobie ich przestrzennej budowy. W podręczniku widzimy rysunki, ale jak przełożyć je na coś, co można dotknąć, obracać, rozkładać? Tutaj kluczem jest wizualizacja i praktyczne podejście.

Figury Obrotowe: Kręcące Się Kształty

Zacznijmy od figur obrotowych. Nazwa sama w sobie sugeruje, że coś się kręci. I rzeczywiście! Figury te powstają w wyniku obrotu figury płaskiej wokół osi.

Walec: Zwykły, ale Ważny

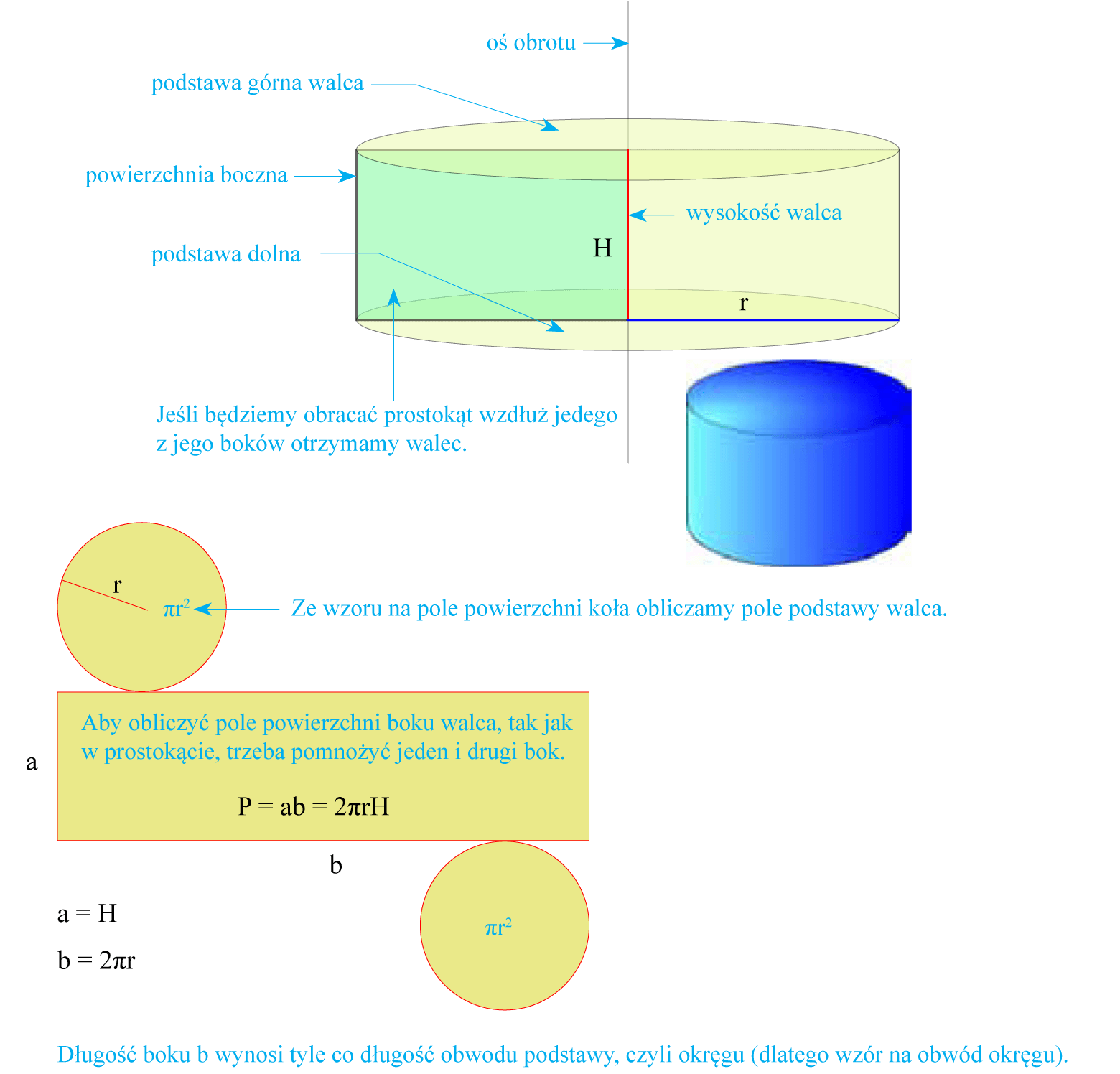
Wyobraź sobie prostokąt. Teraz obróć go wokół jednego z boków. Co powstaje? Walec! To właśnie tak tworzy się ta powszechnie znana bryła. Pomyśl o puszce konserwowej, kubku, albo świecy. Ich kształt to walec.

Kluczowe elementy walca to:

Podstawy: Dwie równe koła.
Powierzchnia boczna: Powstaje z obrotu prostokąta. Jej rozwinięciem jest prostokąt.
Wysokość (H): Odległość między podstawami.
Promień podstawy (r): Promień koła, które tworzy podstawę.

Na sprawdzianie często pojawiają się zadania dotyczące pola powierzchni całkowitej walca (suma pól obu podstaw i pola powierzchni bocznej) oraz objętości walca. Wzory są następujące:

Pole powierzchni całkowitej (Pc) = 2 * Pole podstawy (Pp) + Pole powierzchni bocznej (Pb)

Pp = π * r²

Pb = obwód podstawy * wysokość = 2 * π * r * H

Pc = 2 * π * r² + 2 * π * r * H

Objętość (V) = Pole podstawy * wysokość = π * r² * H

Pamiętaj, że π (pi) to stała matematyczna, w przybliżeniu równa 3,14.

Stożek: Spiczasty Przyjaciel

Teraz wyobraź sobie trójkąt prostokątny. Obróć go wokół jednej z przyprostokątnych. Powstanie stożek! Kojarzy się z czapeczką urodzinową, albo lodami w wafelku (choć to tylko część stożka).

Kluczowe elementy stożka:

Podstawa: Koło.
Wierzchołek: Punkt na osi obrotu.
Wysokość (H): Odległość od wierzchołka do środka podstawy.
Promień podstawy (r): Promień koła.
Tworząca (l): Odcinek łączący wierzchołek z punktem na brzegu podstawy. Tworząca jest dłuższa od wysokości.

Między wysokością, promieniem a tworzącą istnieje zależność wynikająca z twierdzenia Pitagorasa: l² = r² + H². Jest to niezwykle ważne przy obliczeniach!

Wzory na stożek:

Pole powierzchni całkowitej (Pc) = Pole podstawy (Pp) + Pole powierzchni bocznej (Pb)

Pp = π * r²

Pb = π * r * l

Pc = π * r² + π * r * l

Objętość (V) = (1/3) * Pole podstawy * wysokość = (1/3) * π * r² * H

Zauważ, że objętość stożka jest trzykrotnie mniejsza od objętości walca o tych samych wymiarach!

Kula: Idealna Piłka

Na koniec figura obrotowa, którą zna każdy: kula. Powstaje przez obrót półkola wokół jego średnicy.

Kluczowy element kuli:

Promień (r): Odległość od środka kuli do dowolnego punktu na jej powierzchni.

Wzory na kulę:

Pole powierzchni (P) = 4 * π * r²

Objętość (V) = (4/3) * π * r³

Widzisz, jak proste są wzory na kulę? Kluczem jest tylko znajomość promienia.

Wielościany: Geometryczne Budowle

Teraz przenieśmy się do świata wielościanów. To bryły, których powierzchnia składa się z wielokątów – zwanych ścianami. Wielościany są „płaskie” na powierzchni, nie mają krzywizn jak figury obrotowe.

Graniastosłupy: Budujemy z Podstaw

Najprostszymi wielościanami są graniastosłupy. Wyobraź sobie dwa identyczne wielokąty płaskie, ułożone równolegle jeden nad drugim. Połącz ich odpowiednie wierzchołki odcinkami. To są krawędzie boczne, które tworzą ściany boczne (zazwyczaj prostokąty lub równoległoboki).

Kluczowe elementy graniastosłupa:

Podstawy: Dwa identyczne, równoległe wielokąty.
Ściany boczne: Wielokąty (najczęściej prostokąty) łączące boki podstaw.
Krawędzie podstawy: Boki wielokątów tworzących podstawy.
Krawędzie boczne: Odcinki łączące wierzchołki odpowiadających sobie podstaw. W graniastosłupie prostym krawędzie boczne są prostopadłe do podstaw.
Wysokość (H): Odległość między podstawami.

Najczęściej spotykane są:

Graniastosłup trójkątny (podstawa to trójkąt).
Graniastosłup czworokątny (podstawa to czworokąt – np. prostopadłościan lub sześcian).

Prostopadłościan to graniastosłup, którego podstawą jest prostokąt, a wszystkie ściany boczne są prostokątami. Jego wymiary to długość (a), szerokość (b) i wysokość (c). Wzory:

Objętość (V) = a * b * c

Pole powierzchni całkowitej (Pc) = 2 * (ab + bc + ac)

Sześcian to szczególny przypadek prostopadłościanu, gdzie wszystkie krawędzie są równe (a). Wzory:

Objętość (V) = a³

Pole powierzchni całkowitej (Pc) = 6 * a²

Wzór ogólny na objętość każdego graniastosłupa:

Objętość (V) = Pole podstawy (Pp) * Wysokość (H)

Natomiast pole powierzchni całkowitej to suma pól obu podstaw i wszystkich pól ścian bocznych.

Ostrosłupy: Ku Jednemu Wierzchołkowi

Ostrosłupy to bryły, których podstawą jest wielokąt, a wszystkie ściany boczne zbiegają się w jednym punkcie zwanym wierzchołkiem.

Kluczowe elementy ostrosłupa:

Podstawa: Wielokąt.
Wierzchołek: Punkt, do którego zbiegają się wszystkie ściany boczne.
Ściany boczne: Trójkąty.
Wysokość (H): Odcinek od wierzchołka do płaszczyzny podstawy (prostopadły do niej).
Wysokość ściany bocznej (hs): Wysokość trójkąta tworzącego ścianę boczną (zwana też apotemą).

Najczęściej spotykane są:

Ostrosłup trójkątny (podstawa to trójkąt – nazywany też czworościanem).
Ostrosłup czworokątny (podstawa to czworokąt).

Wzór na objętość ostrosłupa:

Objętość (V) = (1/3) * Pole podstawy (Pp) * Wysokość (H)

Ponownie widzimy zależność 1/3! Objętość ostrosłupa jest trzykrotnie mniejsza od objętości graniastosłupa o tej samej podstawie i wysokości.

Pole powierzchni całkowitej ostrosłupa to suma pola podstawy i pól wszystkich jego ścian bocznych.

Jak Się Przygotować do Sprawdzianu? Praktyczne Wskazówki

Teraz, gdy znamy podstawy, czas na strategię nauki!

1. Wizualizuj i Rysuj

Nie ograniczaj się do patrzenia na rysunki w książce. Spróbuj rysować figury samodzielnie. Używaj linijki i cyrkla. Kiedy uczysz się o walcu, pomyśl o kubku. Kiedy o stożku – o czubku czapki. Rysowanie pomaga zapamiętać kształt i proporcje.

2. Twórz Modele

To jeden z najskuteczniejszych sposobów! Możesz użyć:

Plasteliny lub masy solnej: Ulep walec, stożek, sześcian.
Papieru i nożyczek: Wytnij rozwinięcia brył z papieru i złóż je. W internecie znajdziesz gotowe szablony do wydrukowania. Rozwijanie wielościanów na płaszczyźnie to świetne ćwiczenie!
Przedmiotów codziennego użytku: Puszka po napoju to walec, pudełko po butach to prostopadłościan.

3. Ucz się Wzorów ze Zrozumieniem

Nie próbuj zapamiętywać wzorów na ślepo. Zrozum, skąd się biorą. Dlaczego pole powierzchni bocznej walca to obwód podstawy razy wysokość? Bo rozwijając ją, otrzymujesz prostokąt o tych właśnie wymiarach! Dlaczego w objętości ostrosłupa jest 1/3? To już głębsza matematyka, ale warto wiedzieć, że ma ona swoje podstawy. Zapisuj wzory kilkakrotnie, próbuj je odtworzyć z pamięci.

4. Rozwiązuj Zadania – Od Prostych do Trudnych

Zacznij od zadań, gdzie mamy podane wszystkie wymiary i trzeba tylko podstawić do wzoru. Stopniowo przechodź do zadań, gdzie trzeba np. najpierw obliczyć wysokość z twierdzenia Pitagorasa, albo promień z pola powierzchni. Nie zniechęcaj się, jeśli coś nie wyjdzie od razu. Matematyka wymaga cierpliwości i powtarzania.

5. Używaj Kolorów

Kiedy rozwiązujesz zadania, podkreślaj dane, których masz, i te, których szukasz. Używaj różnych kolorów do oznaczenia wymiarów (np. czerwony dla promienia, niebieski dla wysokości). To pomaga w organizacji myśli.

6. Grupa Wsparcia

Ucz się z kolegami lub koleżankami! Wspólne rozwiązywanie zadań, tłumaczenie sobie nawzajem trudniejszych kwestii, to doskonała metoda nauki. Czasem wystarczy, że ktoś Ci coś wytłumaczy innymi słowami.

7. Odpoczynek jest Ważny!

Nie ucz się do późna w nocy. Mózg potrzebuje odpoczynku, aby przetworzyć nowe informacje. Zrób sobie przerwy, wyjdź na spacer, przewietrz pokój. Dobrze wypoczęty umysł lepiej pracuje.

Statystyka i Opinie Ekspertów (dla Ciekawskich)

Badania przeprowadzone przez różne instytucje edukacyjne często wskazują, że uczniowie mają największe trudności z przedmiotami, które wymagają silnej wyobraźni przestrzennej. Właśnie dlatego tak ważne jest, aby przy nauce brył stosować metody wizualne i praktyczne. Profesorowie dydaktyki matematyki podkreślają, że zrozumienie geometrii przestrzennej nie tylko pomaga w nauce matematyki, ale rozwija też zdolności logicznego myślenia i rozwiązywania problemów, które są kluczowe w wielu dziedzinach życia.

Pamiętaj, że każda umiejętność, również ta matematyczna, wymaga czasu i zaangażowania. Figury obrotowe i wielościany mogą wydawać się skomplikowane, ale z odpowiednim podejściem staną się dla Ciebie znacznie łatwiejsze do zrozumienia, a nawet fascynujące. Powodzenia na sprawdzianie!