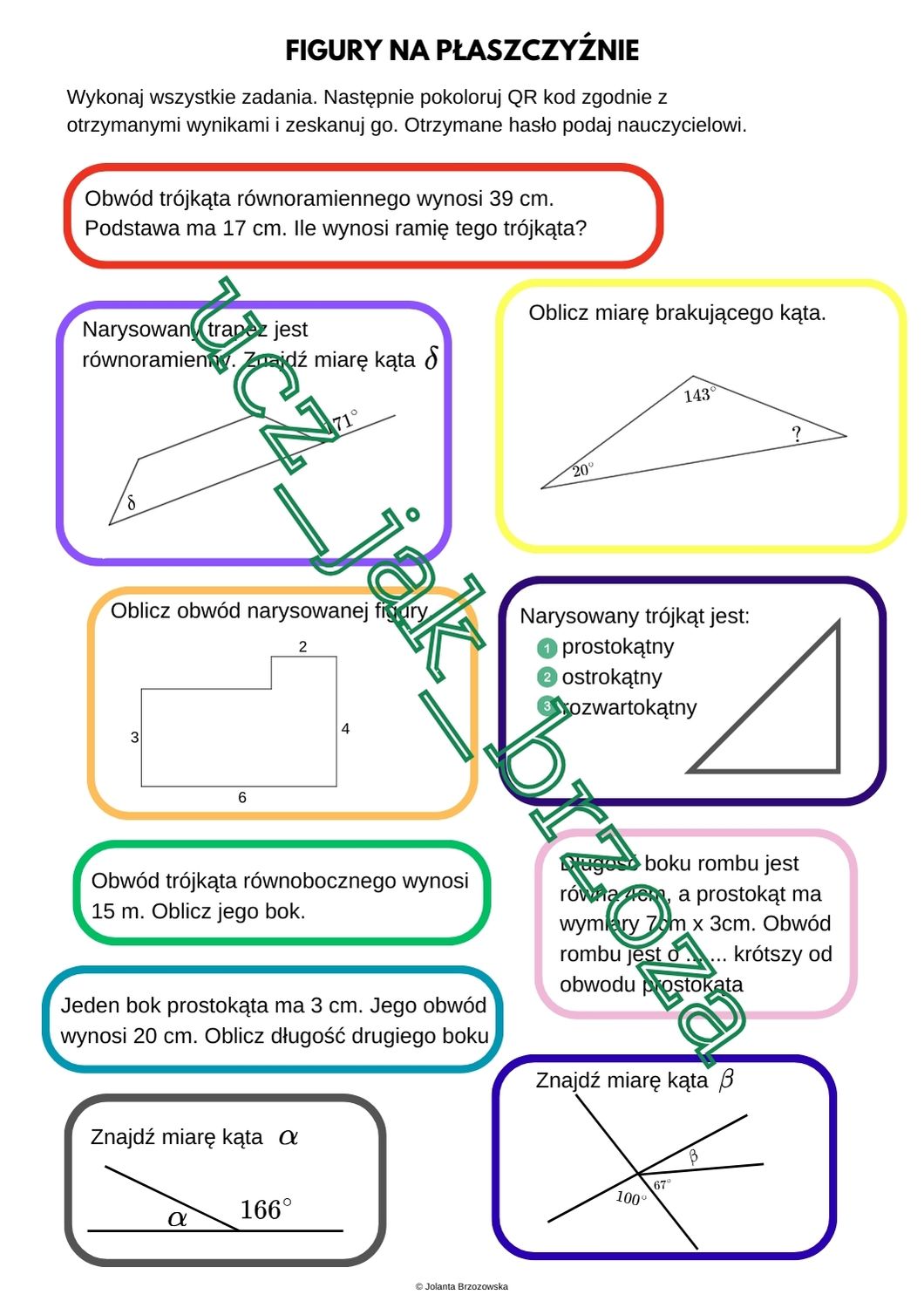
Figury Na Płaszczyźnie Klasa 8 Powtórzenie

Czy geometria spędza Ci sen z powiek? A może zbliża się ważny sprawdzian z figur na płaszczyźnie w klasie 8, a Ty czujesz, że potrzebujesz solidnej powtórki? Jeśli tak, to jesteś we właściwym miejscu! Ten artykuł powstał właśnie z myślą o Tobie – ósmoklasiście, który chce usystematyzować swoją wiedzę i bez stresu podejść do egzaminu.

Naszym celem jest kompleksowe powtórzenie wiadomości na temat figur na płaszczyźnie, które omawiane są w klasie 8. Skupimy się na najważniejszych definicjach, wzorach i zadaniach, które najczęściej pojawiają się na sprawdzianach i kartkówkach. Przygotuj się na solidną dawkę wiedzy, która pomoże Ci zrozumieć i zapamiętać kluczowe informacje!

Podstawowe figury geometryczne i ich własności

Zacznijmy od podstaw. Co to w ogóle jest figura geometryczna? Najprościej mówiąc, to zbiór punktów na płaszczyźnie, który ma określone cechy. W klasie 8 poznajecie wiele różnych figur, a my przypomnimy sobie te najważniejsze:

Prosta i odcinek

• Prosta: Linia, która nie ma początku ani końca i rozciąga się w nieskończoność w obu kierunkach.
• Odcinek: Część prostej ograniczona dwoma punktami, zwanymi końcami odcinka.

Pamiętaj o oznaczeniach! Prostą oznaczamy zwykle małą literą (np. k), a odcinek dwoma dużymi literami (np. AB), gdzie A i B to końce odcinka.

Kąty

Kąt to figura utworzona przez dwie półproste wychodzące z jednego punktu, zwanego wierzchołkiem kąta. Kąty mierzymy w stopniach (°).

Rozróżniamy następujące rodzaje kątów:

• Kąt ostry: Mniejszy niż 90°.
• Kąt prosty: Ma 90°.
• Kąt rozwarty: Większy niż 90° i mniejszy niż 180°.
• Kąt półpełny: Ma 180°.
• Kąt pełny: Ma 360°.

Pamiętaj o kątach przyległych (mają wspólne ramię i wierzchołek, a ich suma wynosi 180°) oraz kątach wierzchołkowych (powstają przez przecięcie się dwóch prostych i są sobie równe).

Wielokąty

Wielokąt to figura ograniczona łamaną zamkniętą. Najważniejsze wielokąty, które musisz znać:

• Trójkąt: Wielokąt o trzech bokach.
• Czworokąt: Wielokąt o czterech bokach.

Szczególne rodzaje trójkątów

Trójkąty możemy klasyfikować ze względu na długość boków i miary kątów:

• Ze względu na boki:
  • Trójkąt równoboczny: Ma wszystkie boki równe.
  • Trójkąt równoramienny: Ma dwa boki równe.
  • Trójkąt różnoboczny: Ma wszystkie boki różnej długości.
• Ze względu na kąty:
  • Trójkąt ostrokątny: Ma wszystkie kąty ostre.
  • Trójkąt prostokątny: Ma jeden kąt prosty.
  • Trójkąt rozwartokątny: Ma jeden kąt rozwarty.

Ważna zależność: Suma kątów w każdym trójkącie wynosi 180°.

Twierdzenie Pitagorasa

To jedno z najważniejszych twierdzeń w geometrii, które dotyczy trójkątów prostokątnych. Mówi ono, że suma kwadratów długości przyprostokątnych (boków leżących przy kącie prostym) jest równa kwadratowi długości przeciwprostokątnej (boku leżącego naprzeciwko kąta prostego).

Wzór: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Czworokąty – rodzaje i własności

Czworokąty to wielokąty o czterech bokach. Do najważniejszych należą:

• Równoległobok: Ma dwie pary boków równoległych.
• Prostokąt: Równoległobok, który ma wszystkie kąty proste.
• Kwadrat: Prostokąt, który ma wszystkie boki równe.
• Romb: Równoległobok, który ma wszystkie boki równe.
• Trapez: Ma przynajmniej jedną parę boków równoległych.
• Deltoid: Ma dwie pary boków sąsiednich równych.

Pamiętaj o własnościach poszczególnych czworokątów. Na przykład: przekątne w prostokącie są równe i przecinają się w połowie, a przekątne w rombie przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy.

Pola i obwody figur

Umiejętność obliczania pól i obwodów figur to podstawa. Przypomnijmy sobie wzory:

Trójkąt

• Pole trójkąta: P = (a * h) / 2, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę. Można również użyć wzoru Herona, jeśli znamy długości wszystkich boków.
• Obwód trójkąta: O = a + b + c, gdzie a, b i c to długości boków.

Kwadrat

• Pole kwadratu: P = a², gdzie a to długość boku.
• Obwód kwadratu: O = 4 * a, gdzie a to długość boku.

Prostokąt

• Pole prostokąta: P = a * b, gdzie a i b to długości boków.
• Obwód prostokąta: O = 2 * (a + b), gdzie a i b to długości boków.

Równoległobok

• Pole równoległoboku: P = a * h, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.
• Obwód równoległoboku: O = 2 * (a + b), gdzie a i b to długości boków.

Romb

• Pole rombu: P = (e * f) / 2, gdzie e i f to długości przekątnych. Można również użyć wzoru P = a * h, gdzie a to długość boku, a h to wysokość.
• Obwód rombu: O = 4 * a, gdzie a to długość boku.

Trapez

• Pole trapezu: P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość.
• Obwód trapezu: O = a + b + c + d, gdzie a i b to długości podstaw, a c i d to długości ramion.

Okrąg i koło

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które są oddalone o daną odległość (promień) od danego punktu (środka okręgu). Koło to okrąg wraz z wnętrzem.

• Promień (r): Odległość od środka okręgu do dowolnego punktu na okręgu.
• Średnica (d): Odcinek przechodzący przez środek okręgu i łączący dwa punkty na okręgu. Średnica jest dwa razy dłuższa od promienia (d = 2r).
• Liczba Pi (π): Stała matematyczna, która w przybliżeniu wynosi 3,14.

Wzory

• Długość okręgu: L = 2 * π * r = π * d
• Pole koła: P = π * r²

Przykładowe zadania i rozwiązania

Teraz przejdźmy do praktyki! Rozwiążmy kilka przykładowych zadań, aby zobaczyć, jak wykorzystać zdobytą wiedzę.

Zadanie 1: Oblicz pole trójkąta prostokątnego, którego przyprostokątne mają długości 6 cm i 8 cm.

Rozwiązanie: P = (6 cm * 8 cm) / 2 = 24 cm².

Zadanie 2: Obwód kwadratu wynosi 36 cm. Oblicz jego pole.

Rozwiązanie: Długość boku kwadratu: a = 36 cm / 4 = 9 cm. Pole kwadratu: P = (9 cm)² = 81 cm².

Zadanie 3: Oblicz długość okręgu o promieniu 5 cm. Przyjmij π ≈ 3,14.

Rozwiązanie: L = 2 * 3,14 * 5 cm = 31,4 cm.

Zadanie 4: Oblicz pole trapezu, którego podstawy mają długości 10 cm i 6 cm, a wysokość wynosi 4 cm.

Rozwiązanie: P = ((10 cm + 6 cm) * 4 cm) / 2 = 32 cm².

Wskazówki i triki

Podsumowanie

Uff, to była spora dawka wiedzy! Mamy nadzieję, że ten artykuł pomógł Ci usystematyzować wiadomości na temat figur na płaszczyźnie. Pamiętaj, że geometria to nie tylko wzory i definicje, ale przede wszystkim logiczne myślenie i umiejętność rozwiązywania problemów. Ćwicz regularnie, a geometria przestanie być Twoim koszmarem, a stanie się fascynującą przygodą! Powodzenia na sprawdzianie!