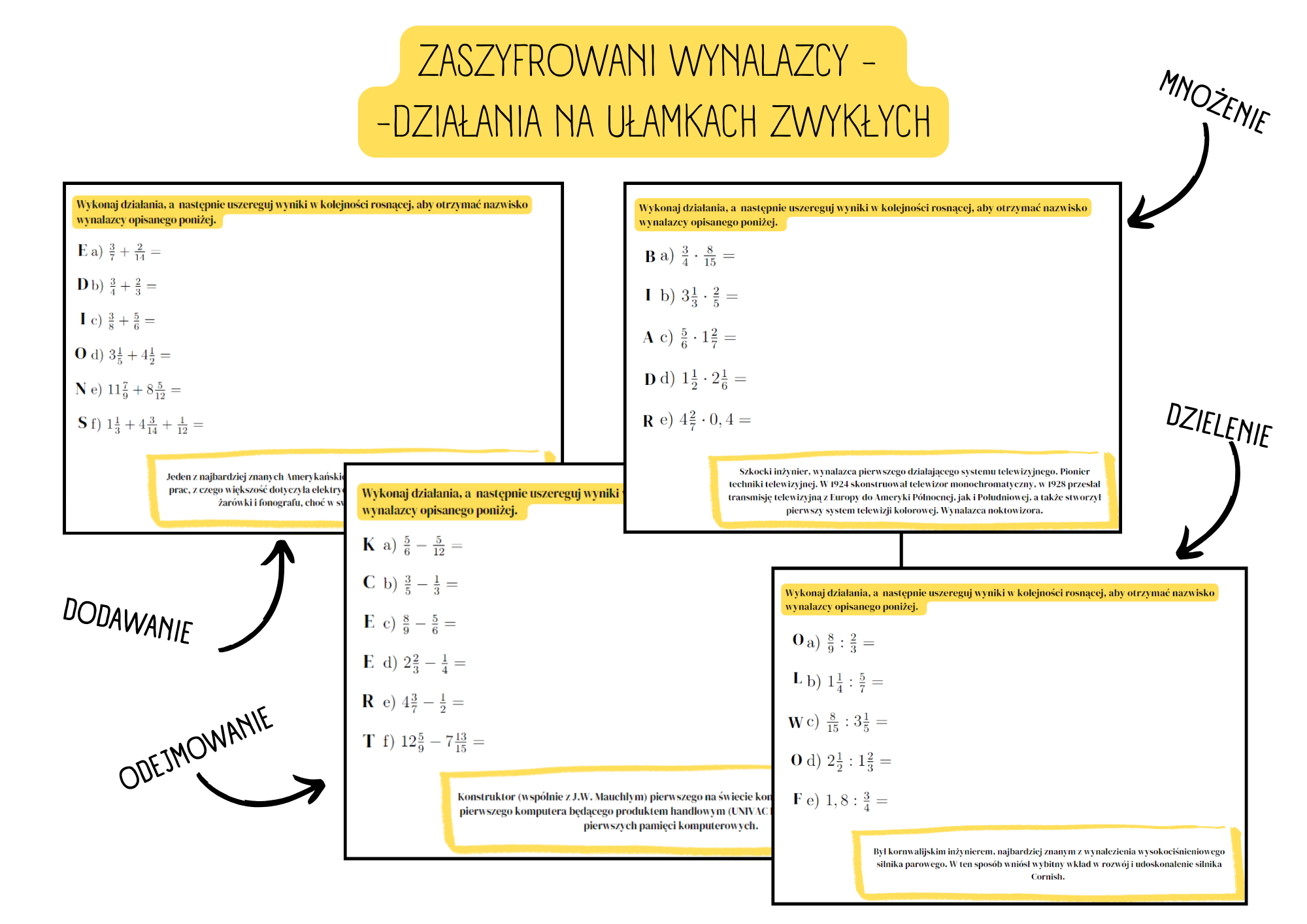
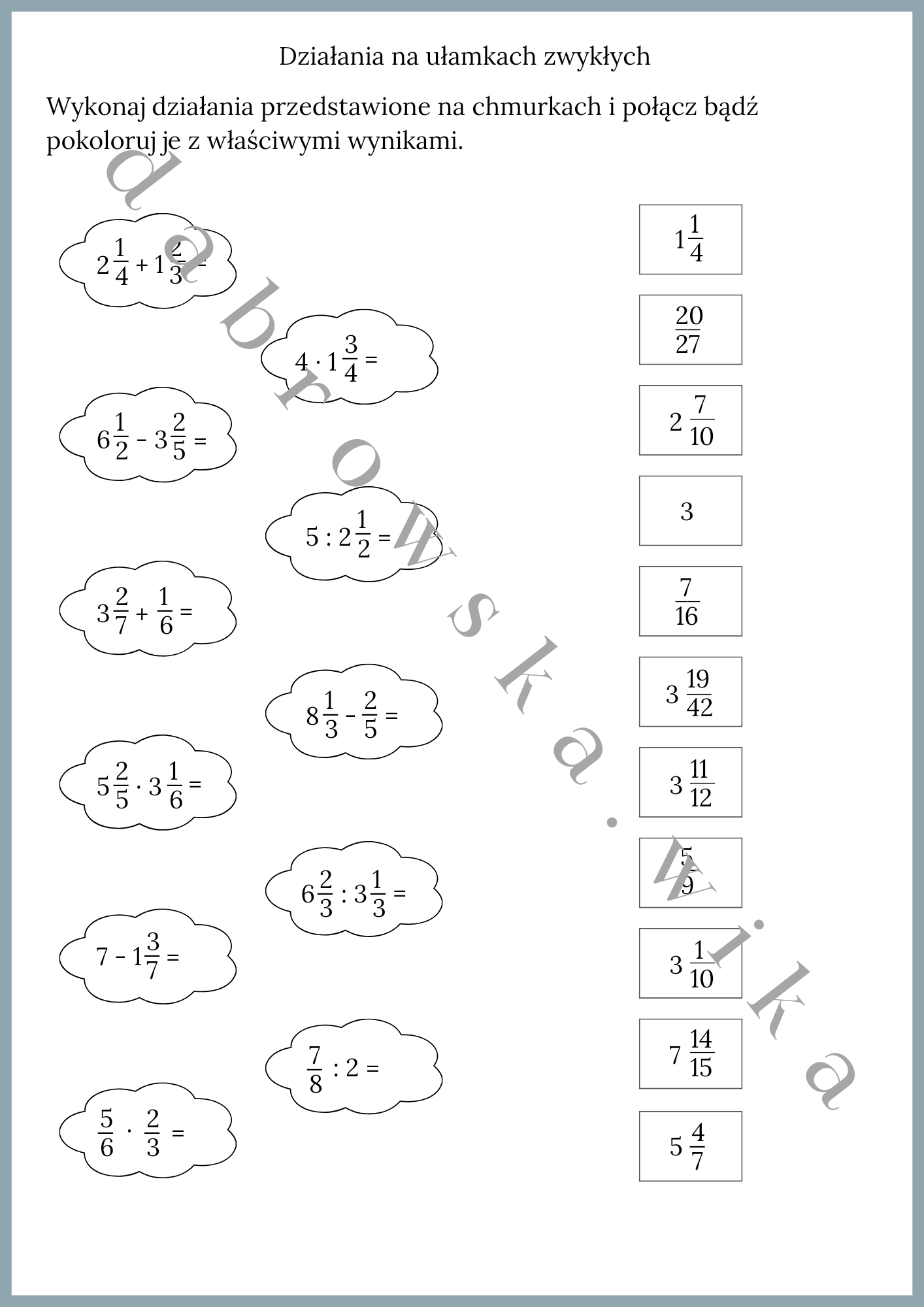
Witajcie, drodzy uczniowie klasy piątej! Przygotujcie się na ekscytującą podróż po świecie ułamków zwykłych! Ułamki towarzyszą nam na co dzień, choć często nie zdajemy sobie z tego sprawy. W tym artykule zgłębimy tajniki działań na ułamkach zwykłych, omówimy najważniejsze zasady i pokażemy, jak rozwiązywać zadania, które na Was czekają. Gotowi? Zaczynamy!
Podstawy Ułamków Zwykłych: Przypomnienie
Zanim przejdziemy do działań, przypomnijmy sobie, czym właściwie jest ułamek zwykły. Ułamek zwykły składa się z licznika (liczba nad kreską ułamkową) i mianownika (liczba pod kreską ułamkową). Mianownik informuje nas, na ile równych części podzielono całość, a licznik mówi, ile z tych części bierzemy pod uwagę.
Na przykład, w ułamku 3/4, mianownik (4) mówi, że całość podzielono na cztery równe części, a licznik (3) mówi, że bierzemy trzy z tych części. Proste, prawda?
Rodzaje Ułamków Zwykłych
Wyróżniamy kilka rodzajów ułamków zwykłych:
- Ułamki właściwe: Licznik jest mniejszy od mianownika (np. 1/2, 2/5, 7/10).
- Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi (np. 5/3, 7/7, 11/4).
- Liczby mieszane: Składają się z liczby całkowitej i ułamka właściwego (np. 11/2, 23/4, 51/3).
Pamiętajcie, że ułamek niewłaściwy można zawsze zamienić na liczbę mieszaną i odwrotnie. To bardzo przydatna umiejętność!
Dodawanie i Odejmowanie Ułamków Zwykłych
Dodawanie i odejmowanie ułamków zwykłych jest bardzo proste, jeśli ułamki mają ten sam mianownik. Wystarczy wtedy dodać (lub odjąć) liczniki, a mianownik pozostaje bez zmian.
Na przykład: 2/5 + 1/5 = (2+1)/5 = 3/5
A co, jeśli ułamki mają różne mianowniki? Wtedy musimy je najpierw sprowadzić do wspólnego mianownika. Najczęściej wykorzystujemy do tego najmniejszą wspólną wielokrotność (NWW) mianowników.
Sprowadzanie do Wspólnego Mianownika
Powiedzmy, że mamy dodać ułamki 1/3 i 1/4. Mianowniki to 3 i 4. Szukamy NWW liczb 3 i 4. Wielokrotności liczby 3 to: 3, 6, 9, 12, 15... Wielokrotności liczby 4 to: 4, 8, 12, 16... Najmniejsza wspólna wielokrotność to 12.
Teraz musimy rozszerzyć każdy ułamek tak, aby miał mianownik równy 12:
1/3 = (1*4)/(3*4) = 4/12
1/4 = (1*3)/(4*3) = 3/12
Teraz możemy dodać ułamki: 4/12 + 3/12 = 7/12
Pamiętaj! Zawsze sprawdzaj, czy otrzymany ułamek da się skrócić. Skracanie ułamków polega na dzieleniu licznika i mianownika przez ten sam dzielnik.
Mnożenie Ułamków Zwykłych
Mnożenie ułamków zwykłych jest jeszcze prostsze niż dodawanie! Wystarczy pomnożyć licznik przez licznik i mianownik przez mianownik.
Na przykład: 2/3 * 1/4 = (2*1)/(3*4) = 2/12. Otrzymany ułamek możemy skrócić, dzieląc licznik i mianownik przez 2: 2/12 = 1/6
Jeśli mnożymy ułamek przez liczbę całkowitą, możemy potraktować liczbę całkowitą jako ułamek z mianownikiem równym 1. Na przykład: 3 * 1/2 = 3/1 * 1/2 = 3/2 = 11/2
Dzielenie Ułamków Zwykłych
Dzielenie ułamków zwykłych to nic innego jak mnożenie przez odwrotność! Aby podzielić ułamek przez inny ułamek, mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Odwrotność ułamka powstaje przez zamianę licznika z mianownikiem.
Na przykład, odwrotnością ułamka 3/5 jest 5/3.
Zatem, jeśli chcemy podzielić 1/2 przez 3/4, robimy to tak:
1/2 : 3/4 = 1/2 * 4/3 = (1*4)/(2*3) = 4/6 = 2/3
Zadania Tekstowe z Ułamkami – Jak je Rozwiązywać?
Wiele osób ma problem z zadaniami tekstowymi, które zawierają ułamki. Kluczem do sukcesu jest uważne przeczytanie zadania i zrozumienie, co trzeba obliczyć.
Oto kilka kroków, które pomogą Wam w rozwiązywaniu zadań tekstowych z ułamkami:
- Przeczytaj uważnie zadanie. Zwróć uwagę na wszystkie liczby i informacje.
- Zidentyfikuj, co masz obliczyć. Jakie jest pytanie zadane w zadaniu?
- Zapisz dane w postaci ułamków. Jeśli to możliwe, zamień liczby mieszane na ułamki niewłaściwe.
- Ustal, jakie działanie (dodawanie, odejmowanie, mnożenie, dzielenie) musisz wykonać. Spróbuj wyobrazić sobie sytuację opisaną w zadaniu.
- Wykonaj obliczenia. Pamiętaj o kolejności wykonywania działań.
- Sprawdź, czy wynik ma sens. Czy Twój wynik jest logiczny w kontekście zadania?
- Zapisz odpowiedź. Odpowiedz na pytanie zadane w zadaniu pełnym zdaniem.
Przykłady Zadań Tekstowych
Przykład 1: Mama upiekła pizzę i podzieliła ją na 8 równych kawałków. Tomek zjadł 3/8 pizzy, a Kasia 2/8 pizzy. Ile pizzy zjedli razem Tomek i Kasia?
Rozwiązanie:
Tomek zjadł 3/8 pizzy.
Kasia zjadła 2/8 pizzy.
Razem zjedli: 3/8 + 2/8 = 5/8 pizzy.
Odpowiedź: Tomek i Kasia zjedli razem 5/8 pizzy.
Przykład 2: Ania ma 1/2 tabliczki czekolady. Podzieliła ją równo pomiędzy 3 koleżanki. Jaką część tabliczki czekolady dostała każda koleżanka?
Rozwiązanie:
Ania ma 1/2 tabliczki czekolady.
Dzieli ją na 3 części, czyli 1/2 : 3 = 1/2 : 3/1 = 1/2 * 1/3 = 1/6
Odpowiedź: Każda koleżanka dostała 1/6 tabliczki czekolady.
Ułamki w Życiu Codziennym – Przykłady
Jak już wspomniałem, ułamki towarzyszą nam na co dzień. Oto kilka przykładów:
- Gotowanie: Przepisy często podają składniki w ułamkach (np. 1/2 szklanki mąki, 1/4 łyżeczki soli).
- Zakupy: Często kupujemy produkty na wagę, np. 1/2 kg jabłek, 3/4 kg sera.
- Czas: Mówimy "pół godziny" (1/2 godziny), "kwadrans" (1/4 godziny).
- Sport: W wynikach sportowych często pojawiają się ułamki (np. drużyna wygrała 2/3 meczów).
- Pieniądze: 50 groszy to 1/2 złotego.
Wyobraźcie sobie, że pieczecie ciasto. Przepis wymaga 3/4 szklanki cukru, ale macie tylko miarkę o pojemności 1/4 szklanki. Ile razy musicie napełnić miarkę, aby odmierzyć potrzebną ilość cukru? Odpowiedź to 3 razy (3/4 podzielone przez 1/4 to 3)!
Albo inny przykład: Chcecie podzielić pizzę na 6 osób, ale macie tylko 1/2 pizzy. Jaką część całej pizzy otrzyma każda osoba? Odpowiedź to 1/12 (1/2 podzielone przez 6 to 1/12)!
Podsumowanie i Zachęta do Działania
Gratulacje! Dotarliście do końca tego artykułu. Mam nadzieję, że działania na ułamkach zwykłych nie są już dla Was takie straszne. Pamiętajcie, że kluczem do sukcesu jest ćwiczenie. Im więcej zadań rozwiążecie, tym lepiej zrozumiecie zasady i nabierzecie pewności siebie.
Nie bójcie się pytać, jeśli macie jakieś wątpliwości. Nauczyciel i koledzy z klasy na pewno Wam pomogą. A jeśli nadal czujecie się niepewnie, wróćcie do tego artykułu i przeczytajcie go jeszcze raz. Powodzenia!
Zachęcam Was do poszukiwania przykładów zastosowania ułamków w Waszym otoczeniu. Zwróćcie uwagę na przepisy kulinarne, etykiety produktów, wyniki sportowe i inne sytuacje, w których pojawiają się ułamki. Im lepiej zrozumiecie, jak ułamki działają w praktyce, tym łatwiej będzie Wam rozwiązywać zadania i korzystać z nich w życiu codziennym.