Działania Na Ułamkach Zwykłych I Dziesiętnych Sprawdzian Klasa 6

Witaj! Przygotowujesz się do sprawdzianu z działań na ułamkach zwykłych i dziesiętnych w klasie 6? Świetnie! Ten artykuł pomoże Ci usystematyzować wiedzę i poczuć się pewniej.
Zacznijmy od ułamków zwykłych. Ułamek zwykły składa się z licznika (liczba na górze) i mianownika (liczba na dole). Na przykład, w ułamku 3/4, 3 to licznik, a 4 to mianownik. Mianownik mówi nam, na ile części całość została podzielona, a licznik - ile takich części bierzemy.
Dodawanie i odejmowanie ułamków zwykłych wymaga sprowadzenia ich do wspólnego mianownika. Oznacza to znalezienie najmniejszej wspólnej wielokrotności (NWW) mianowników. Na przykład, aby dodać 1/2 i 1/3, musimy znaleźć NWW liczb 2 i 3, która wynosi 6. Wtedy 1/2 zamieniamy na 3/6, a 1/3 na 2/6. Teraz możemy dodać: 3/6 + 2/6 = 5/6.
Mnożenie ułamków zwykłych jest prostsze. Mnożymy licznik przez licznik, a mianownik przez mianownik. Na przykład: 2/5 * 3/7 = 6/35. Pamiętaj, że przed mnożeniem warto sprawdzić, czy można coś skrócić.
Dzielenie ułamków zwykłych polega na pomnożeniu pierwszego ułamka przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem. Na przykład: 1/4 : 2/3 = 1/4 * 3/2 = 3/8.
Teraz przejdźmy do ułamków dziesiętnych. Ułamek dziesiętny to liczba, która ma część całkowitą i część ułamkową oddzielone przecinkiem. Na przykład: 3,14. Każda cyfra po przecinku reprezentuje dziesiąte, setne, tysięczne itd. części całości.
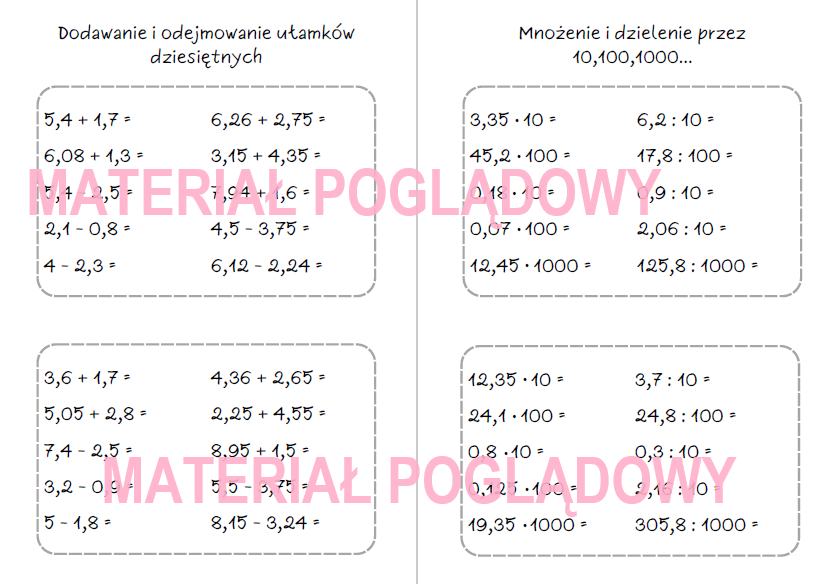
Dodawanie i odejmowanie ułamków dziesiętnych wykonujemy pisemnie, pamiętając o wyrównaniu przecinków. Wtedy dodajemy lub odejmujemy cyfry w odpowiednich kolumnach. Na przykład: 1,25 + 2,3 = 3,55.
Mnożenie ułamków dziesiętnych również wykonujemy pisemnie, ignorując na początku przecinki. Po pomnożeniu liczymy, ile łącznie cyfr jest po przecinku w obu mnożonych liczbach. Tyle samo cyfr oddzielamy przecinkiem w wyniku. Na przykład: 2,5 * 1,2 = 3,00 (jedna cyfra po przecinku w 2,5 i jedna cyfra po przecinku w 1,2, więc łącznie dwie cyfry po przecinku w wyniku).
Dzielenie ułamków dziesiętnych przez liczbę naturalną wykonujemy pisemnie. Jeśli dzielimy przez ułamek dziesiętny, przesuwamy przecinek w dzielniku i dzielnej o tyle miejsc w prawo, aby dzielnik stał się liczbą naturalną. Na przykład: 4,5 : 0,5 = 45 : 5 = 9.
Zamiana ułamków zwykłych na dziesiętne polega na podzieleniu licznika przez mianownik. Na przykład: 1/4 = 1 : 4 = 0,25. Niektóre ułamki zwykłe mają rozwinięcie dziesiętne skończone (np. 1/2 = 0,5), a inne - nieskończone okresowe (np. 1/3 = 0,333...).
Zamiana ułamków dziesiętnych na zwykłe polega na zapisaniu ułamka dziesiętnego w postaci ułamka zwykłego z mianownikiem 10, 100, 1000 itd., a następnie uproszczeniu go. Na przykład: 0,75 = 75/100 = 3/4.
Ćwicz regularnie! Rozwiązuj zadania z podręcznika i zeszytu ćwiczeń. Pamiętaj, że praktyka czyni mistrza! Powodzenia na sprawdzianie!