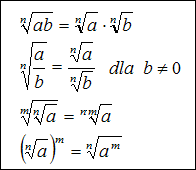Działania Na Pierwiastkach Ii Gimnazjum Sprawdzian

Witajcie, drodzy uczniowie drugich klas gimnazjum! Dziś zajmiemy się tematem, który może na początku wydawać się trochę straszny, ale w rzeczywistości jest bardzo logiczny i przydatny. Chodzi o działania na pierwiastkach. To fundament do dalszych, ciekawszych zagadnień matematycznych, więc warto zrozumieć to dobrze.
Zacznijmy od podstaw. Czym właściwie jest pierwiastek? Pierwiastek kwadratowy z danej liczby to taka liczba, która podniesiona do kwadratu (pomnożona przez siebie) daje nam tę pierwotną liczbę. Na przykład, pierwiastek kwadratowy z 9 to 3, ponieważ 3 * 3 = 9. Zapisujemy to jako √9 = 3. Podobnie, √16 = 4, bo 4 * 4 = 16.
Teraz przejdźmy do konkretnych działań. Pierwszym i bardzo ważnym działaniem jest mnożenie pierwiastków. Zasada jest prosta: możemy pomnożyć liczby pod pierwiastkami, a wynik zapisać pod jednym wspólnym pierwiastkiem. Czyli, jeśli mamy √a * √b, możemy to zapisać jako √(a * b). Przykład: √2 * √8 = √(2 * 8) = √16 = 4. To bardzo ułatwia obliczenia!
Kolejnym działaniem jest dzielenie pierwiastków. Tutaj zasada jest analogiczna do mnożenia. Możemy podzielić liczby pod pierwiastkami i wynik zapisać pod jednym pierwiastkiem. Czyli, jeśli mamy √a / √b, to jest to równe √(a / b). Przykład: √25 / √4 = √(25 / 4) = √6.25 = 2.5. Pamiętajmy, że nigdy nie dzielimy przez pierwiastek z zera.
Ciekawym zagadnieniem jest również wyciąganie liczby przed pierwiastek. Czasami liczba pod pierwiastkiem nie jest idealnym kwadratem, ale możemy ją uprościć, wyciągając z niej kwadrat jakiegoś czynnika. Na przykład, √12. Możemy zapisać 12 jako 4 * 3. Wtedy √12 = √(4 * 3) = √4 * √3 = 2√3. Liczba 2 została wyciągnięta przed pierwiastek. Im więcej takich uproszczeń zrobimy, tym łatwiej będzie nam operować na pierwiastkach.
Dodawanie i odejmowanie pierwiastków jest możliwe tylko wtedy, gdy pierwiastki są "podobne", czyli mają tę samą liczbę pod pierwiastkiem. Możemy wtedy dodać lub odjąć liczby stojące przed pierwiastkami. Na przykład, 3√2 + 5√2 = (3+5)√2 = 8√2. Ale nie możemy dodać 3√2 + 5√3, bo liczby pod pierwiastkami są różne.
Dlaczego te działania są ważne? Pierwiastki pojawiają się wszędzie w matematyce, od geometrii (twierdzenie Pitagorasa!) po algebrę. Zrozumienie działań na pierwiastkach pozwala nam upraszczać skomplikowane wyrażenia, rozwiązywać równania, a nawet obliczać odległości czy pola powierzchni w bardziej złożonych zadaniach.
Pamiętajcie, że praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej opanujecie te umiejętności. Nie bójcie się pytać, jeśli coś jest niejasne. Powodzenia na sprawdzianie!