Druga Zasada Dynamiki Dla Ruchu Obrotowego

Czy kiedykolwiek czułeś, że fizyka jest jak mur nie do przebicia? Szczególnie ruch obrotowy potrafi sprawiać trudności. Ale wierz mi, nie jesteś sam! Wiele osób boryka się z tym tematem, ale zrozumienie Drugiej Zasady Dynamiki dla ruchu obrotowego, choć początkowo wydaje się skomplikowane, jest kluczem do opanowania fizyki. Postaramy się tutaj rozłożyć to zagadnienie na czynniki pierwsze i pokazać, że fizyka wcale nie musi być straszna!

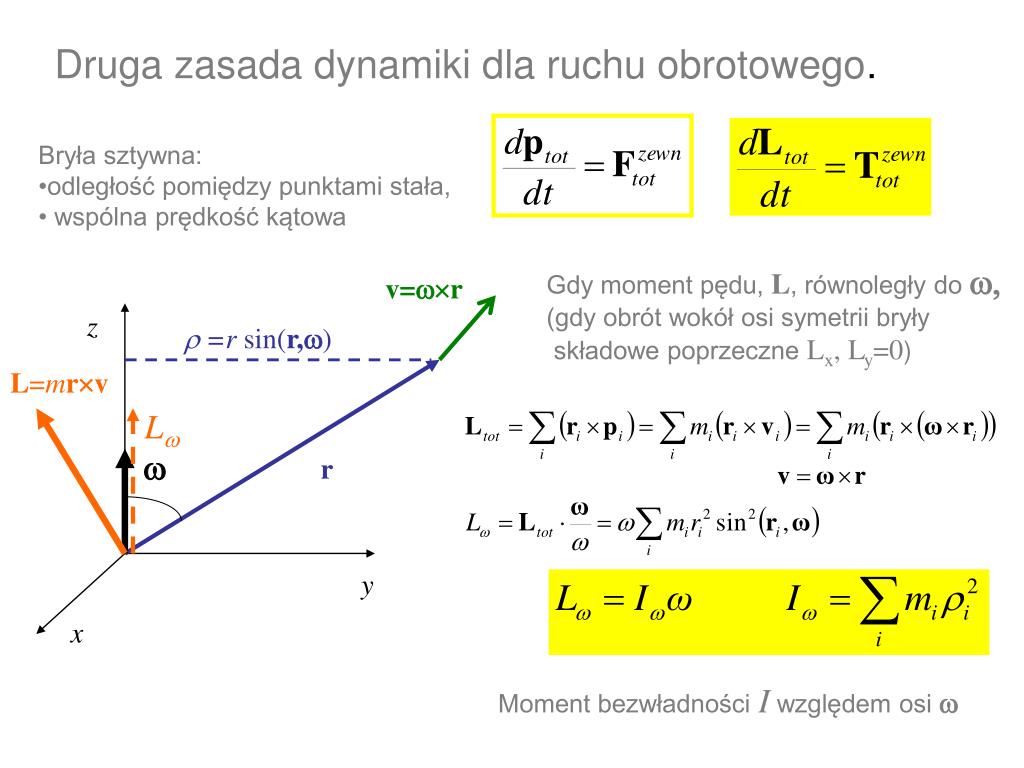
Czym jest Druga Zasada Dynamiki dla ruchu obrotowego?

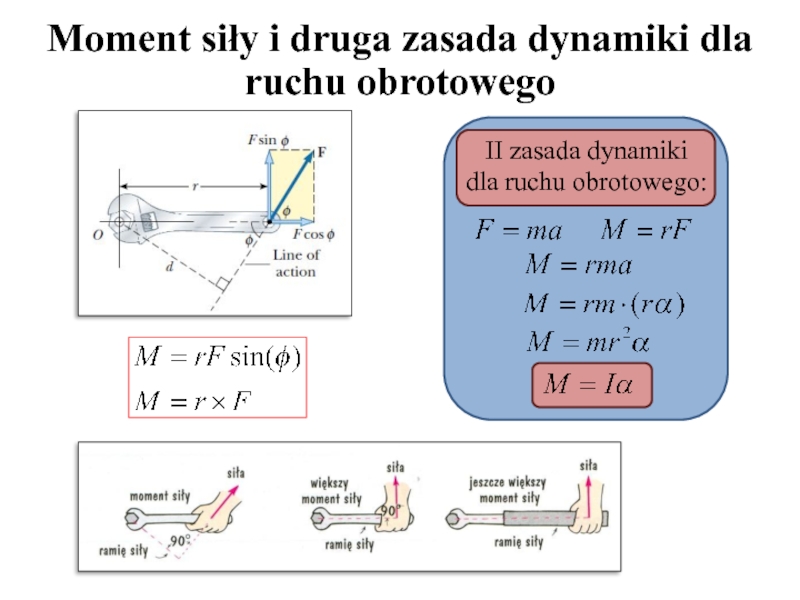
Zacznijmy od podstaw. Pamiętasz Drugą Zasadę Dynamiki Newtona dla ruchu postępowego? F = ma (siła równa się masie razy przyspieszenie). Druga Zasada Dynamiki dla ruchu obrotowego jest jej odpowiednikiem, ale dotyczy obiektów, które się obracają. Zamiast siły, mamy moment siły, zamiast masy – moment bezwładności, a zamiast przyspieszenia liniowego – przyspieszenie kątowe.

Wzór wygląda następująco: M = Iα, gdzie:

• M – to moment siły (mierzony w niutonometrach – Nm), który powoduje obrót. Myśl o nim jako o "skręcaniu" obiektu.
• I – to moment bezwładności (mierzony w kilogramach razy metr kwadratowy – kg·m²), który reprezentuje opór obiektu przed zmianą jego ruchu obrotowego. To taka "masa obrotowa".
• α – to przyspieszenie kątowe (mierzone w radianach na sekundę kwadrat – rad/s²), czyli jak szybko zmienia się prędkość obrotowa obiektu.

Kluczowe różnice między ruchem postępowym i obrotowym:

• W ruchu postępowym ciało przesuwa się w linii prostej, a w ruchu obrotowym kręci się wokół osi.
• Siła powoduje przyspieszenie liniowe, a moment siły powoduje przyspieszenie kątowe.
• Masa reprezentuje opór przed zmianą ruchu postępowego, a moment bezwładności reprezentuje opór przed zmianą ruchu obrotowego.

Pomyśl o otwieraniu drzwi. Im dalej od zawiasów naciskasz, tym łatwiej je otworzyć. To właśnie dlatego, że zwiększasz moment siły. Moment siły zależy nie tylko od samej siły, ale też od odległości od osi obrotu. Im większa odległość, tym większy moment siły, a więc łatwiej wprawić obiekt w ruch obrotowy (lub zatrzymać go).

Moment bezwładności – co to takiego?

Moment bezwładności to miara tego, jak trudno jest zmienić prędkość obrotową danego obiektu. Nie jest to stała wartość – zależy od masy obiektu i sposobu jej rozmieszczenia względem osi obrotu.

Wyobraź sobie dwa walce o tej samej masie. Jeden jest pełny, a drugi to pusta rura. Który łatwiej rozkręcić? Pełny walec ma mniejszy moment bezwładności, bo jego masa jest bardziej skupiona bliżej osi obrotu. Pustą rurę trudniej rozkręcić, bo masa jest bardziej oddalona od osi.

Dla różnych kształtów i osi obrotu moment bezwładności oblicza się różnie. Istnieją gotowe wzory dla podstawowych brył, takie jak:

• Punktowa masa w odległości r od osi: I = mr²
• Walec pełny obracający się wokół swojej osi: I = ½mr²
• Obręcz obracająca się wokół swojej osi: I = mr²
• Kula pełna obracająca się wokół swojej osi: I = (2/5)mr²

Gdzie 'm' to masa, a 'r' to promień.

Zrozumienie momentu bezwładności jest kluczowe do projektowania urządzeń i maszyn. Na przykład, koła zamachowe w silnikach mają duży moment bezwładności, aby utrzymać stałą prędkość obrotową.

Przykłady i zastosowania

Druga Zasada Dynamiki dla ruchu obrotowego ma mnóstwo zastosowań w życiu codziennym i w inżynierii:

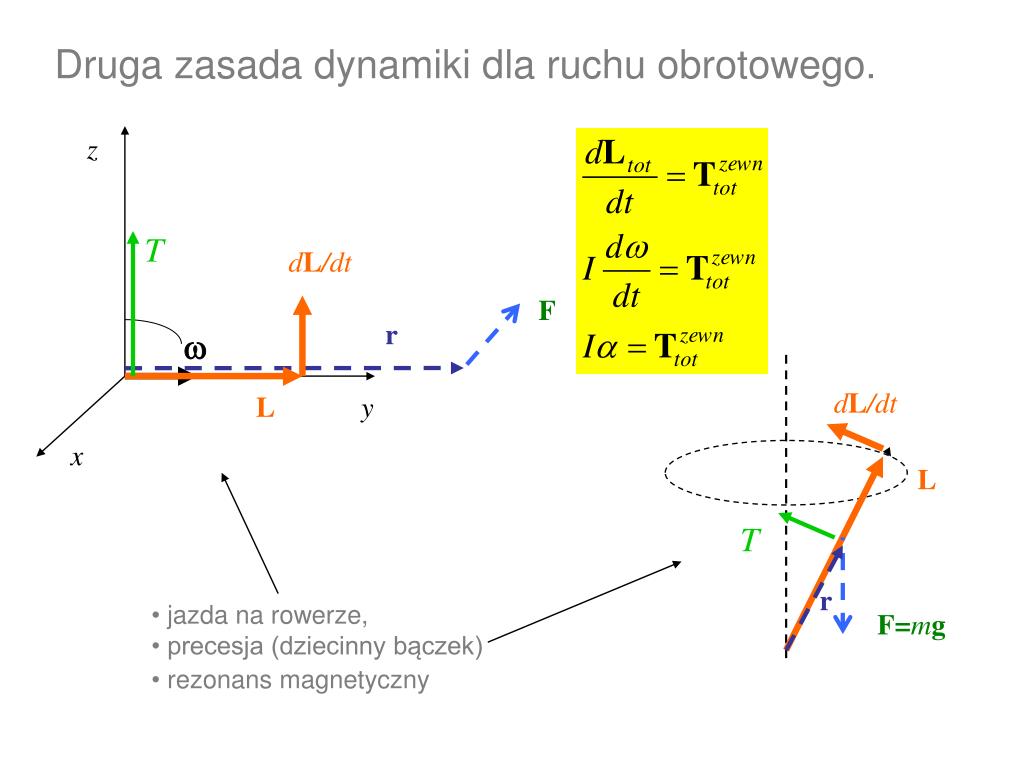
• Rower: Kiedy naciskasz na pedały, generujesz moment siły, który obraca korbą. Im większy moment siły, tym większe przyspieszenie kątowe kół.
• Samochód: Silnik generuje moment siły, który napędza koła. Inżynierowie muszą uwzględniać moment bezwładności różnych części, aby zapewnić płynną jazdę.
• Wiertarka: Silnik wiertarki generuje moment siły, który obraca wiertło. Im większy moment siły, tym łatwiej wiercić w twardych materiałach.
• Karuzela: Aby karuzela zaczęła się kręcić, potrzebny jest moment siły. Dzieci, odpychając się nogami, dostarczają ten moment.

Przykład obliczeniowy: Wyobraź sobie, że próbujesz rozkręcić koło o momencie bezwładności 2 kg·m². Działasz na nie momentem siły 5 Nm. Jakie będzie przyspieszenie kątowe koła?

Używamy wzoru M = Iα. Przekształcamy go: α = M / I = 5 Nm / 2 kg·m² = 2.5 rad/s².

Oznacza to, że prędkość obrotowa koła będzie rosła o 2.5 radiana na sekundę, co sekundę.

Jak efektywnie uczyć i uczyć się Drugiej Zasady Dynamiki dla ruchu obrotowego?

Oto kilka praktycznych wskazówek dla nauczycieli, uczniów i rodziców:

• Dla nauczycieli:
  • Zacznij od demonstracji: Użyj prostych eksperymentów z obracającymi się przedmiotami, aby wizualizować koncepcje momentu siły i momentu bezwładności.
  • Użyj analogii: Porównuj ruch obrotowy z ruchem postępowym, aby ułatwić zrozumienie.
  • Daj dużo przykładów: Pokaż, jak Druga Zasada Dynamiki dla ruchu obrotowego jest stosowana w różnych dziedzinach.
  • Zachęcaj do rozwiązywania problemów: Daj uczniom możliwość rozwiązywania zadań, aby utrwalić wiedzę.
  • Wykorzystaj technologie: Użyj symulacji komputerowych, aby pokazać ruch obrotowy w interaktywny sposób.
• Dla uczniów:
  • Zacznij od podstaw: Upewnij się, że rozumiesz podstawowe pojęcia, takie jak siła, masa i przyspieszenie.
  • Rób notatki: Zapisuj wzory i definicje, aby móc do nich wracać.
  • Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz materiał.
  • Szukaj pomocy: Nie bój się pytać nauczyciela lub kolegów o pomoc, jeśli masz trudności.
  • Stosuj wiedzę w praktyce: Spróbuj znaleźć przykłady ruchu obrotowego w swoim otoczeniu.
• Dla rodziców:
  • Zainteresuj dziecko fizyką: Pokaż dziecku, jak fizyka jest obecna w życiu codziennym.
  • Pomagaj w rozwiązywaniu zadań: Jeśli potrafisz, pomóż dziecku w rozwiązywaniu zadań z fizyki.
  • Stwórz sprzyjające środowisko do nauki: Zapewnij dziecku ciche miejsce do nauki i dostęp do materiałów edukacyjnych.
  • Pochwal wysiłki: Doceniaj starania dziecka, nawet jeśli nie zawsze osiąga sukcesy.

Pułapki i częste błędy

Warto być świadomym typowych błędów, które popełniają uczniowie podczas nauki Drugiej Zasady Dynamiki dla ruchu obrotowego:

• Mylenie siły z momentem siły: Pamiętaj, że moment siły to siła działająca na pewnej odległości od osi obrotu.
• Niewłaściwe obliczanie momentu bezwładności: Upewnij się, że używasz właściwego wzoru dla danego kształtu i osi obrotu.
• Zapominanie o jednostkach: Upewnij się, że wszystkie jednostki są spójne (np. niutonometry dla momentu siły, kilogramy razy metr kwadratowy dla momentu bezwładności, radiany na sekundę kwadrat dla przyspieszenia kątowego).
• Błędne interpretowanie znaku przyspieszenia kątowego: Przyspieszenie kątowe może być dodatnie (przyspieszenie) lub ujemne (opóźnienie).

Wskazówka: Zawsze rysuj diagramy sił i momentów sił, aby lepiej zrozumieć problem.

Inspiracja i motywacja

Fizyka, a w szczególności Druga Zasada Dynamiki dla ruchu obrotowego, to nie tylko zbiór wzorów i definicji. To fascynujące narzędzie do zrozumienia, jak działa świat wokół nas. Dzięki niej możemy projektować lepsze maszyny, budować bardziej wydajne silniki i odkrywać nowe zjawiska w kosmosie.

Pamiętaj, że nauka fizyki to proces, który wymaga czasu i wysiłku. Nie zrażaj się trudnościami, ale traktuj je jako wyzwania, które pomogą Ci się rozwinąć. Z każdym rozwiązanym zadaniem, z każdym zrozumianym pojęciem, stajesz się coraz bardziej pewny siebie i kompetentny.

Wierz w siebie i w swoje możliwości! Sukces w nauce fizyki jest w zasięgu Twojej ręki. Powodzenia!