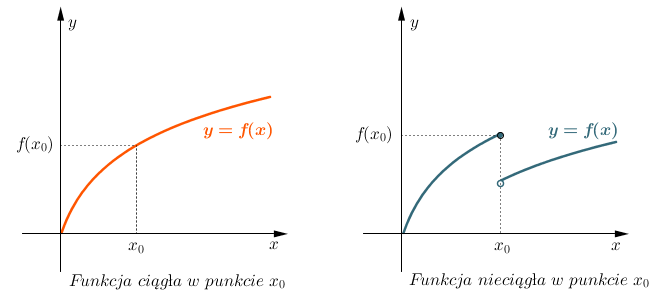Co To Znaczy że Funkcja Jest Różniczkowalna

Hej! Zastanawiałeś/aś się kiedyś, co to znaczy, że funkcja jest różniczkowalna? To brzmi skomplikowanie, ale postaram się to wyjaśnić w prosty sposób. Chodź, zanurkujmy w ten temat!
Zacznijmy od podstaw. Funkcja to po prostu przepis, który przypisuje każdemu argumentowi (x) jakąś wartość (y). Wyobraź sobie automat z napojami. Wrzucasz monetę (x), a automat wydaje napój (y). To jest właśnie funkcja!
Kluczowym pojęciem jest pochodna funkcji. Pochodna w danym punkcie to nic innego jak współczynnik kierunkowy stycznej do wykresu funkcji w tym punkcie. Brzmi strasznie? Spokojnie! Pomyśl o jeździe na rowerze pod górę. Pochodna to stromość zbocza w danym miejscu. Im większa pochodna, tym stromsze zbocze.
Teraz, co to znaczy, że funkcja jest różniczkowalna w punkcie? To znaczy, że w tym punkcie istnieje pochodna, czyli możemy wyznaczyć współczynnik kierunkowy stycznej. Innymi słowy, wykres funkcji w tym punkcie jest "gładki", bez żadnych ostrych kantów czy przerw. Wyobraź sobie gładki, zakrzywiony tor wyścigowy – możesz jechać płynnie i skręcać bez problemu.
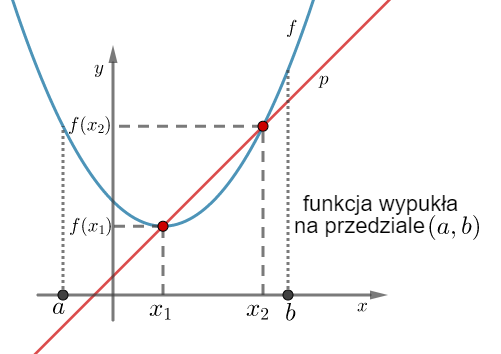
Jeśli funkcja jest różniczkowalna w każdym punkcie pewnego przedziału, to mówimy, że jest różniczkowalna na tym przedziale. To znaczy, że możemy obliczyć pochodną w każdym punkcie tego przedziału. Funkcja jest "gładka" na całym tym przedziale. Pomyśl o drodze z równym asfaltem – jazda jest komfortowa na całej długości.
Przykłady funkcji różniczkowalnych: Wielomiany (np. x2 + 3x - 1), funkcje sinus i cosinus, funkcje eksponencjalne (np. ex). Te funkcje mają "gładkie" wykresy, bez ostrych kantów.
A co z funkcjami, które nie są różniczkowalne? Weźmy wartość bezwzględną (|x|). W punkcie x = 0 ma "ostry kant". Nie możemy jednoznacznie określić współczynnika kierunkowego stycznej. Inny przykład to funkcja, która ma "przerwę" w swoim wykresie – w tym punkcie również nie jest różniczkowalna.
Ważne jest, żeby pamiętać, że różniczkowalność implikuje ciągłość. To znaczy, że jeśli funkcja jest różniczkowalna w punkcie, to musi być w tym punkcie ciągła (bez przerw). Ale uwaga! Nie działa to w drugą stronę. Funkcja może być ciągła, ale nie musi być różniczkowalna (np. wartość bezwzględna w x = 0).
Podsumowując, różniczkowalność mówi nam o tym, jak "gładka" jest funkcja. Daje nam możliwość obliczenia pochodnej, która z kolei informuje nas o tempie zmian funkcji. To ważne narzędzie w matematyce i fizyce, pozwalające analizować różne procesy i zjawiska. Mam nadzieję, że teraz to pojęcie jest dla Ciebie bardziej zrozumiałe!