Co To Jest Miejsce Zerowe Funkcji Liniowej

Funkcje liniowe są jednymi z podstawowych pojęć w matematyce, a ich zrozumienie jest kluczowe do dalszego studiowania algebry i analizy. Jednym z fundamentalnych aspektów funkcji liniowej jest jej miejsce zerowe. Co to takiego i jak je znaleźć? Niniejszy artykuł ma na celu kompleksowe wyjaśnienie tego zagadnienia, od definicji, przez metody obliczania, aż po praktyczne zastosowania.

Definicja Miejsca Zerowego Funkcji Liniowej

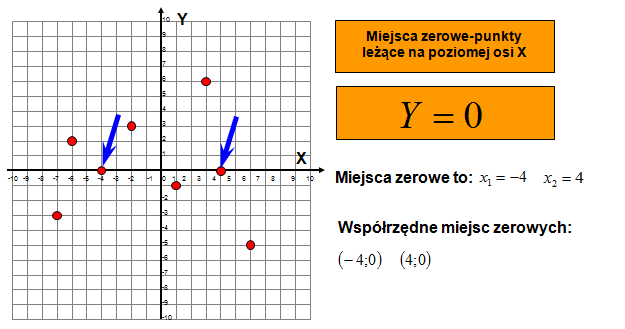
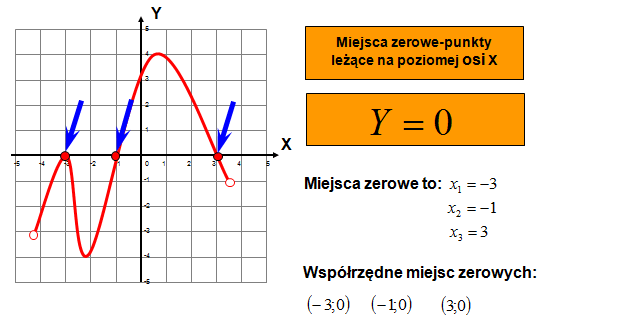
Miejsce zerowe funkcji, niezależnie od jej rodzaju (liniowa, kwadratowa, trygonometryczna, etc.), to argument (wartość x), dla którego funkcja przyjmuje wartość zero (y = 0). Inaczej mówiąc, jest to punkt, w którym wykres funkcji przecina oś OX (oś odciętych). W przypadku funkcji liniowej, poszukiwanie miejsca zerowego sprowadza się do znalezienia takiego 'x', dla którego wartość funkcji 'f(x)' równa się zero.

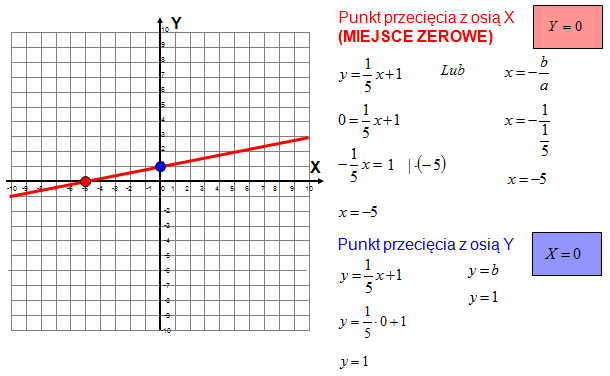
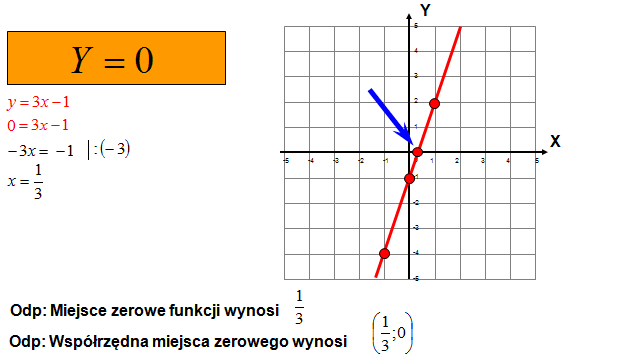
Matematycznie, jeśli mamy funkcję liniową zapisaną jako f(x) = ax + b, gdzie 'a' i 'b' są stałymi (a ≠ 0), to miejsce zerowe to rozwiązanie równania:

ax + b = 0

Zatem, aby znaleźć miejsce zerowe, musimy rozwiązać to proste równanie.

Jak Obliczyć Miejsce Zerowe Funkcji Liniowej?

Krok po Kroku: Rozwiązywanie Równania

Obliczenie miejsca zerowego funkcji liniowej jest stosunkowo proste i wymaga tylko kilku kroków:

Zapisz równanie: Zacznij od zapisania równania funkcji liniowej w postaci f(x) = ax + b. Upewnij się, że znasz wartości 'a' (współczynnik kierunkowy) i 'b' (wyraz wolny).
Podstaw zero za f(x): Zastąp f(x) w równaniu zerem: ax + b = 0.
Przenieś wyraz wolny: Przenieś wyraz wolny 'b' na prawą stronę równania, zmieniając jego znak: ax = -b.
Podziel przez współczynnik kierunkowy: Podziel obie strony równania przez współczynnik kierunkowy 'a': x = -b/a.
Otrzymaj wynik: Otrzymana wartość 'x' jest miejscem zerowym funkcji.

Przykład: Załóżmy, że mamy funkcję liniową f(x) = 2x - 4. Aby znaleźć jej miejsce zerowe, wykonujemy następujące kroki:

Równanie: f(x) = 2x - 4
Podstawienie: 2x - 4 = 0
Przeniesienie: 2x = 4
Podzielenie: x = 4/2
Wynik: x = 2

Zatem, miejscem zerowym funkcji f(x) = 2x - 4 jest x = 2. Oznacza to, że wykres tej funkcji przecina oś OX w punkcie (2, 0).

Specjalne Przypadki

Warto wspomnieć o sytuacjach, w których funkcja liniowa może nie mieć miejsca zerowego lub mieć ich nieskończenie wiele:

Funkcja stała (a = 0 i b ≠ 0): Jeśli współczynnik kierunkowy 'a' jest równy zero, a wyraz wolny 'b' jest różny od zera, to funkcja jest stała i ma postać f(x) = b. W takim przypadku funkcja nigdy nie przyjmuje wartości zero, więc nie posiada miejsca zerowego. Na przykład, funkcja f(x) = 5 nigdy nie przecina osi OX.
Funkcja tożsamościowa (a = 0 i b = 0): Jeśli zarówno 'a' jak i 'b' są równe zero, to funkcja ma postać f(x) = 0. Oznacza to, że funkcja przyjmuje wartość zero dla każdego 'x'. W takim przypadku każda liczba rzeczywista jest miejscem zerowym.

Interpretacja Graficzna

Graficzne przedstawienie funkcji liniowej to linia prosta. Miejsce zerowe odpowiada punktowi, w którym ta linia przecina oś OX. Wizualizacja ta ułatwia zrozumienie, że jeśli linia jest równoległa do osi OX i nie pokrywa się z nią (przypadek funkcji stałej), to nie ma punktu przecięcia, a więc nie ma miejsca zerowego. Z kolei, jeśli linia pokrywa się z osią OX (przypadek funkcji tożsamościowej), to każdy punkt na osi OX jest punktem przecięcia, czyli miejscem zerowym.

Można sobie wyobrazić, że manipulując parametrami 'a' i 'b' w równaniu f(x) = ax + b, zmieniamy nachylenie i położenie linii prostej na wykresie. Zmieniając 'a' kontrolujemy, jak stroma jest linia, a zmieniając 'b' przesuwamy ją w górę lub w dół wzdłuż osi OY. Miejsce zerowe przesuwa się w zależności od tych zmian.

Praktyczne Zastosowania Miejsca Zerowego Funkcji Liniowej

Znajomość miejsca zerowego funkcji liniowej ma wiele praktycznych zastosowań w różnych dziedzinach:

Ekonomia: W analizie kosztów i przychodów, miejsce zerowe funkcji kosztów całkowitych (jeśli ma formę liniową) może reprezentować próg rentowności, czyli punkt, w którym przychody zrównują się z kosztami.
Fizyka: W fizyce, miejsce zerowe funkcji opisującej ruch jednostajny może oznaczać moment, w którym ciało osiąga określone położenie (np. punkt startowy).
Statystyka: W statystyce, w analizie regresji liniowej, miejsce zerowe może pomagać w interpretacji zależności między zmiennymi.
Programowanie: W wielu algorytmach, szczególnie tych związanych z interpolacją liniową lub rozwiązywaniem równań, znajomość miejsc zerowych jest niezbędna do prawidłowego działania.
Finanse: Obliczanie punktu, w którym inwestycja zwraca się.

Przykład z życia wzięty: Wyobraźmy sobie, że prowadzimy małą firmę produkującą ręcznie robione świece. Koszt wytworzenia jednej świecy wynosi 5 zł (koszt materiałów), a sprzedajemy ją po 12 zł. Nasze stałe koszty miesięczne (czynsz, opłaty) wynoszą 500 zł. Możemy stworzyć funkcję liniową opisującą nasz zysk: Zysk(x) = (12 - 5)x - 500 = 7x - 500, gdzie 'x' to liczba sprzedanych świec. Miejsce zerowe tej funkcji (7x - 500 = 0, czyli x = 500/7 ≈ 71.43) powie nam, ile świec musimy sprzedać, aby pokryć wszystkie koszty i wyjść na zero. Musimy więc sprzedać około 72 świece, aby zacząć zarabiać.

Przykład z danymi: Firma analizuje zależność pomiędzy wydatkami na reklamę (x - w tysiącach złotych) a wzrostem sprzedaży (y - w procentach). Z analizy wynika funkcja liniowa: y = 2x - 5. Miejsce zerowe tej funkcji (2x - 5 = 0, czyli x = 2.5) informuje firmę, że minimalne wydatki na reklamę muszą wynieść 2.5 tysiąca złotych, aby w ogóle zaobserwować jakikolwiek wzrost sprzedaży (poniżej tego progu wydatki są nieskuteczne).

Podsumowanie

Miejsce zerowe funkcji liniowej to kluczowe pojęcie, które pozwala zrozumieć, kiedy funkcja przyjmuje wartość zero. Obliczenie miejsca zerowego sprowadza się do rozwiązania prostego równania liniowego. Znajomość tego zagadnienia ma szerokie zastosowanie w wielu dziedzinach, od ekonomii i fizyki, po statystykę i programowanie. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym jest miejsce zerowe funkcji liniowej i jak je obliczać.

Zachęcam do dalszego zgłębiania wiedzy z zakresu matematyki i do szukania zastosowań funkcji liniowych w otaczającym nas świecie. Próbuj rozwiązywać różne zadania i analizować przykłady, aby utrwalić zdobytą wiedzę. Pamiętaj, że praktyka czyni mistrza!