Bryły Obrotowe Sprawdzian 3 Liceum

Witaj! Zbliża się sprawdzian z brył obrotowych w 3. liceum? Wiem, jak stresujące potrafią być takie momenty. To nie tylko "kolejny test", ale sprawdzian Twojej ciężkiej pracy i zrozumienia zagadnień, które, być może, wydają się abstrakcyjne.

Spróbujmy spojrzeć na to z innej strony. Bryły obrotowe to nie tylko wzory do zapamiętania, ale elementy, które otaczają nas w codziennym życiu. Od kubka, z którego pijesz herbatę, po wieże ciśnień i elementy konstrukcji budowlanych. Zrozumienie ich geometrii pozwala lepiej rozumieć świat i rozwiązywać realne problemy. Ten sprawdzian to krok do zdobycia tej wiedzy.

Dlaczego Bryły Obrotowe Są Ważne?

Zanim przejdziemy do konkretnych zadań, warto uświadomić sobie, dlaczego w ogóle się tym zajmujemy. Bryły obrotowe, jak sama nazwa wskazuje, powstają przez obrót figury płaskiej wokół osi. To dość proste, prawda? Ale konsekwencje tego prostego procesu są ogromne:

• Inżynieria: Projektowanie wałów, łożysk, rur, zbiorników – wszystko to opiera się na wiedzy o bryłach obrotowych.
• Architektura: Kopuły, wieże, elementy dekoracyjne – geometria brył obrotowych pozwala na tworzenie pięknych i funkcjonalnych budowli.
• Przemysł: Produkcja opakowań, naczyń, elementów maszyn – znajomość objętości i powierzchni brył obrotowych jest kluczowa dla optymalizacji procesów produkcyjnych.
• Medycyna: Projektowanie protez, implantów, narzędzi chirurgicznych – dokładność i precyzja są tu najważniejsze, a wiedza o bryłach obrotowych pomaga je osiągnąć.

Jak widzisz, to nie tylko suche wzory. To fundament wielu dziedzin, które wpływają na nasze życie.

Jak Uczyć Się Skutecznie?

Zamiast wkuwać wzory na pamięć, spróbuj zrozumieć, skąd się biorą. To znacznie bardziej efektywne i trwalsze. Pamiętaj, wzór to skrótowy zapis pewnej zależności, a nie magiczna formuła. Oto kilka sprawdzonych sposobów:

• Wizualizacja: Wyobraź sobie, jak figura płaska obraca się wokół osi. Zobacz, jak powstaje bryła. Możesz nawet użyć modeliny lub plasteliny, żeby stworzyć fizyczny model.
• Rozwiązywanie zadań krok po kroku: Nie spiesz się. Analizuj każde zadanie, identyfikuj dane i szukaj odpowiednich wzorów. Pisz szczegółowe obliczenia, żeby uniknąć błędów.
• Praca z przykładami: Przejrzyj rozwiązane zadania z podręcznika lub zbioru. Zrozum, jak zostały rozwiązane i spróbuj rozwiązać je samodzielnie, zakrywając rozwiązanie.
• Powtórki: Regularnie wracaj do materiału. Krótkie, ale częste powtórki są lepsze niż długa, ale jednorazowa nauka.
• Grupa wsparcia: Ucz się z kolegami i koleżankami. Tłumaczenie zagadnień innym pomaga utrwalić wiedzę i dostrzec własne braki.

Najczęściej Spotykane Bryły Obrotowe

Na sprawdzianie najprawdopodobniej pojawią się zadania związane z następującymi bryłami:

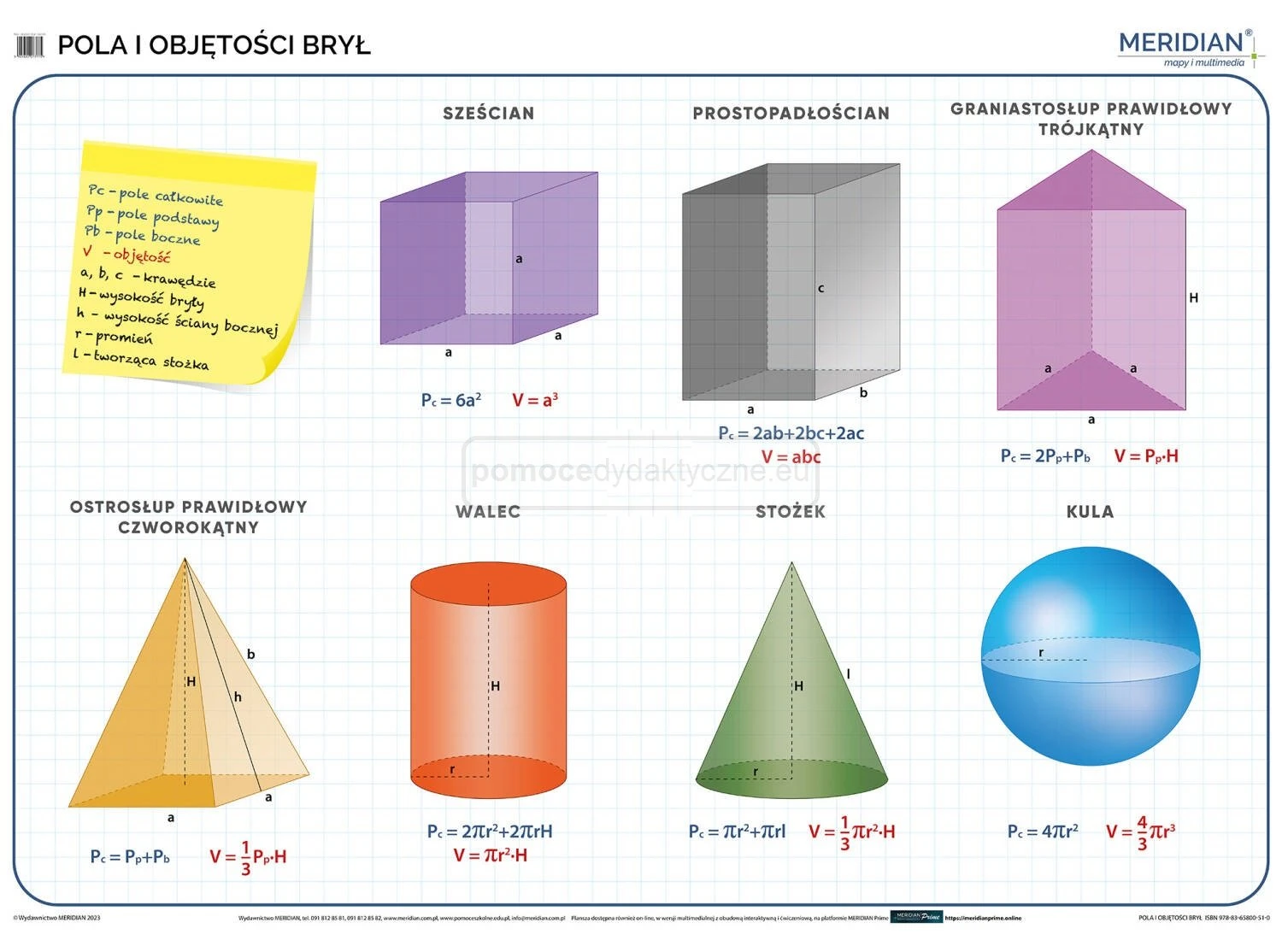
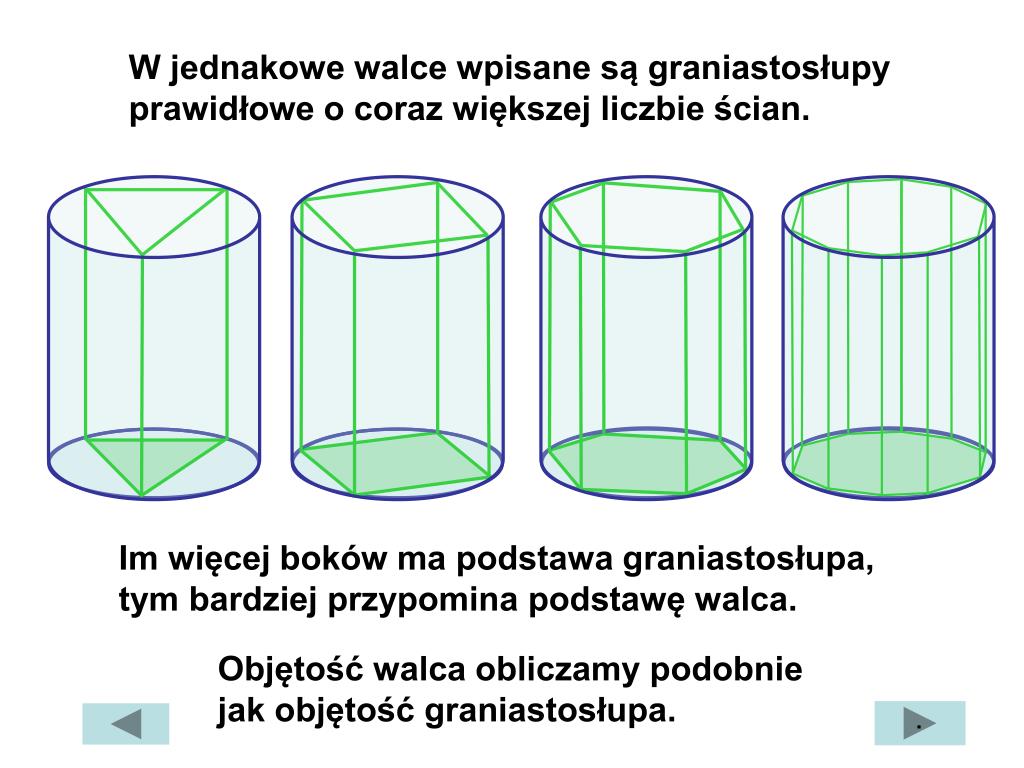
Walec

Powstaje przez obrót prostokąta wokół jednego z jego boków. Kluczowe parametry to promień podstawy (r) i wysokość (h). Wzory:

• Pole powierzchni bocznej: 2πrh
• Pole powierzchni całkowitej: 2πr(r + h)
• Objętość: πr²h

Pamiętaj: Zrozumienie, co oznaczają poszczególne symbole (r, h), jest kluczowe. Zastanów się, jak zmieniają się te parametry i jak wpływają na pole i objętość walca.

Stożek

Powstaje przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych. Kluczowe parametry to promień podstawy (r), wysokość (h) i tworząca (l). Wzory:

• Pole powierzchni bocznej: πrl
• Pole powierzchni całkowitej: πr(r + l)
• Objętość: (1/3)πr²h

Uwaga: Zwróć uwagę na związek między r, h i l. Z twierdzenia Pitagorasa wynika, że l² = r² + h². Często trzeba obliczyć jeden z tych parametrów, znając dwa pozostałe.

Kula

Powstaje przez obrót koła wokół jego średnicy. Kluczowy parametr to promień (r). Wzory:

• Pole powierzchni: 4πr²
• Objętość: (4/3)πr³

Wskazówka: Kula jest najprostszą z tych brył pod względem definicji, ale obliczenia mogą być bardziej skomplikowane, jeśli zadanie dotyczy fragmentów kuli (np. wycinka kulistego).

Przykładowe Zadania i Rozwiązania

Zadanie 1: Oblicz objętość walca, którego promień podstawy wynosi 5 cm, a wysokość 10 cm.

Rozwiązanie:

Objętość walca obliczamy ze wzoru V = πr²h.

Podstawiamy wartości: V = π * (5 cm)² * 10 cm = π * 25 cm² * 10 cm = 250π cm³.

Odpowiedź: Objętość walca wynosi 250π cm³.

Zadanie 2: Stożek ma wysokość 12 cm i tworzącą 13 cm. Oblicz pole powierzchni bocznej stożka.

Rozwiązanie:

Najpierw musimy obliczyć promień podstawy (r). Z twierdzenia Pitagorasa: r² + h² = l², więc r² = l² - h².

r² = (13 cm)² - (12 cm)² = 169 cm² - 144 cm² = 25 cm².

r = √25 cm² = 5 cm.

Pole powierzchni bocznej stożka obliczamy ze wzoru Pb = πrl.

Podstawiamy wartości: Pb = π * 5 cm * 13 cm = 65π cm².

Odpowiedź: Pole powierzchni bocznej stożka wynosi 65π cm².

Zadanie 3: Oblicz pole powierzchni kuli o promieniu 6 cm.

Rozwiązanie:

Pole powierzchni kuli obliczamy ze wzoru P = 4πr².

Podstawiamy wartość: P = 4 * π * (6 cm)² = 4 * π * 36 cm² = 144π cm².

Odpowiedź: Pole powierzchni kuli wynosi 144π cm².

Typowe Pułapki i Jak Ich Unikać

• Błędy w jednostkach: Upewnij się, że wszystkie wymiary są w tej samej jednostce (np. wszystkie w centymetrach). Przedstaw wynik w odpowiedniej jednostce (np. cm² dla pola, cm³ dla objętości).
• Pomylone wzory: Dokładnie sprawdź wzory, zanim je zastosujesz. Warto je zapisać na kartce przed rozpoczęciem rozwiązywania zadań.
• Brak zrozumienia definicji: Upewnij się, że rozumiesz, czym jest promień, wysokość, tworząca. Narysuj sobie rysunek pomocniczy, żeby lepiej to zwizualizować.
• Brak sprawdzania odpowiedzi: Po rozwiązaniu zadania sprawdź, czy odpowiedź ma sens. Czy objętość stożka może być większa od objętości walca o tych samych wymiarach?

A co, jeśli naprawdę nie rozumiem?

To naturalne, że niektóre zagadnienia wydają się trudniejsze od innych. Ważne jest, żeby nie poddawać się. Jeśli masz problemy, spróbuj:

• Zapytać nauczyciela: Nauczyciel jest po to, żeby pomóc. Nie wstydź się zadawać pytań.
• Poszukać pomocy w internecie: Istnieje wiele stron i kanałów YouTube, które tłumaczą zagadnienia matematyczne w prosty sposób.
• Skorzystać z korepetycji: Korepetytor może pomóc Ci indywidualnie i skupić się na Twoich konkretnych problemach.
• Po prostu dać sobie czas: Czasem potrzebujesz po prostu "przespać się" z problemem. Odpocznij, a potem wróć do niego ze świeżym umysłem.

Podsumowanie i Co Dalej?

Pamiętaj, sprawdzian to tylko jeden z etapów nauki. Nie definiuje Twojej wartości. Traktuj go jako szansę na sprawdzenie swojej wiedzy i zidentyfikowanie obszarów, w których potrzebujesz więcej pracy. Zrozumienie brył obrotowych to cenna umiejętność, która przyda Ci się w życiu.

Teraz, gdy masz solidne podstawy, zachęcam Cię do rozwiązania kilku dodatkowych zadań, aby utrwalić swoją wiedzę. Wykorzystaj zasoby online, podręczniki i zbiory zadań. Pamiętaj o wizualizacji i rozumieniu wzorów, a nie tylko o ich wkuwaniu. Poświęć czas na zrozumienie definicji i relacji między poszczególnymi elementami brył. I przede wszystkim – nie stresuj się! Podejdź do sprawdzianu z pewnością siebie i przekonaniem, że dałeś z siebie wszystko.

Jakie konkretne zadanie z brył obrotowych sprawia Ci najwięcej trudności? Może spróbujemy je razem rozwiązać?